PAL: Pluralistic Alignment Framework for Learning from Heterogeneous Preferences

Large foundation models pretrained on raw web-scale data are not readily deployable without additional step of extensive alignment to human preferences. Such alignment is typically done by collecting large amounts of pairwise comparisons from humans ("Do you prefer output A or B?") and learning a reward model or a policy with the Bradley-Terry-Luce (BTL) model as a proxy for a human's underlying implicit preferences. These methods generally suffer from assuming a universal preference shared by all humans, which lacks the flexibility of adapting to plurality of opinions and preferences. In this work, we propose PAL, a framework to model human preference complementary to existing pretraining strategies, which incorporates plurality from the ground up. We propose using the ideal point model as a lens to view alignment using preference comparisons. Together with our novel reformulation and using mixture modeling, our framework captures the plurality of population preferences while simultaneously learning a common preference latent space across different preferences, which can few-shot generalize to new, unseen users. Our approach enables us to use the penultimate-layer representation of large foundation models and simple MLP layers to learn reward functions that are on-par with the existing large state-of-the-art reward models, thereby enhancing efficiency of reward modeling significantly. We show that PAL achieves competitive reward model accuracy compared to strong baselines on 1) Language models with Summary dataset ; 2) Image Generative models with Pick-a-Pic dataset ; 3) A new semisynthetic heterogeneous dataset generated using Anthropic Personas. Finally, our experiments also highlight the shortcoming of current preference datasets that are created using rigid rubrics which wash away heterogeneity, and call for more nuanced data collection approaches.

Taming False Positives in Out-of-Distribution Detection with Human Feedback

Robustness to out-of-distribution (OOD) samples is crucial for safely deploying machine learning models in the open world. Recent works have focused on designing scoring functions to quantify OOD uncertainty. Setting appropriate thresholds for these scoring functions for OOD detection is challenging as OOD samples are often unavailable up front. Typically, thresholds are set to achieve a desired true positive rate (TPR), e.g., $95\%$ TPR. However, this can lead to very high false positive rates (FPR), ranging from 60 to 96\%, as observed in the Open-OOD benchmark. In safety-critical real-life applications, e.g., medical diagnosis, controlling the FPR is essential when dealing with various OOD samples dynamically. To address these challenges, we propose a mathematically grounded OOD detection framework that leverages expert feedback to \emph{safely} update the threshold on the fly. We provide theoretical results showing that it is guaranteed to meet the FPR constraint at all times while minimizing the use of human feedback. Another key feature of our framework is that it can work with any scoring function for OOD uncertainty quantification. Empirical evaluation of our system on synthetic and benchmark OOD datasets shows that our method can maintain FPR at most $5\%$ while maximizing TPR.

Pearls from Pebbles: Improved Confidence Functions for Auto-labeling

Auto-labeling is an important family of techniques that produce labeled training sets with minimum manual labeling. A prominent variant, threshold-based auto-labeling (TBAL), works by finding a threshold on a model's confidence scores above which it can accurately label unlabeled data points. However, many models are known to produce overconfident scores, leading to poor TBAL performance. While a natural idea is to apply off-the-shelf calibration methods to alleviate the overconfidence issue, such methods still fall short. Rather than experimenting with ad-hoc choices of confidence functions, we propose a framework for studying the \emph{optimal} TBAL confidence function. We develop a tractable version of the framework to obtain \texttt{Colander} (Confidence functions for Efficient and Reliable Auto-labeling), a new post-hoc method specifically designed to maximize performance in TBAL systems. We perform an extensive empirical evaluation of our method \texttt{Colander} and compare it against methods designed for calibration. \texttt{Colander} achieves up to 60\% improvements on coverage over the baselines while maintaining auto-labeling error below $5\%$ and using the same amount of labeled data as the baselines.

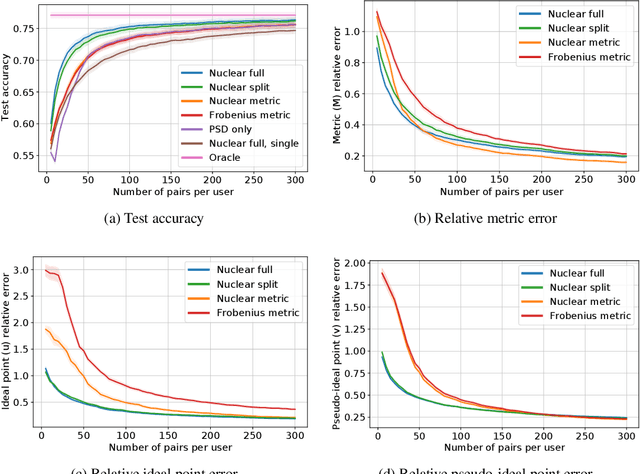
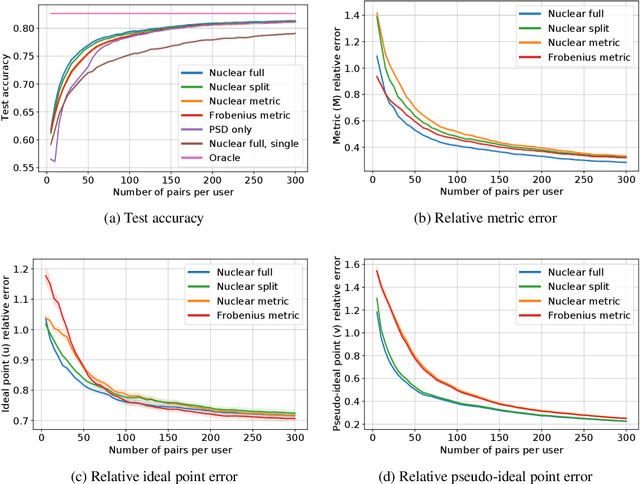
Metric Learning from Limited Pairwise Preference Comparisons

We study metric learning from preference comparisons under the ideal point model, in which a user prefers an item over another if it is closer to their latent ideal item. These items are embedded into $\mathbb{R}^d$ equipped with an unknown Mahalanobis distance shared across users. While recent work shows that it is possible to simultaneously recover the metric and ideal items given $\mathcal{O}(d)$ pairwise comparisons per user, in practice we often have a limited budget of $o(d)$ comparisons. We study whether the metric can still be recovered, even though it is known that learning individual ideal items is now no longer possible. We show that in general, $o(d)$ comparisons reveals no information about the metric, even with infinitely many users. However, when comparisons are made over items that exhibit low-dimensional structure, each user can contribute to learning the metric restricted to a low-dimensional subspace so that the metric can be jointly identified. We present a divide-and-conquer approach that achieves this, and provide theoretical recovery guarantees and empirical validation.

Unbiased Face Synthesis With Diffusion Models: Are We There Yet?

Text-to-image diffusion models have achieved widespread popularity due to their unprecedented image generation capability. In particular, their ability to synthesize and modify human faces has spurred research into using generated face images in both training data augmentation and model performance assessments. In this paper, we study the efficacy and shortcomings of generative models in the context of face generation. Utilizing a combination of qualitative and quantitative measures, including embedding-based metrics and user studies, we present a framework to audit the characteristics of generated faces conditioned on a set of social attributes. We applied our framework on faces generated through state-of-the-art text-to-image diffusion models. We identify several limitations of face image generation that include faithfulness to the text prompt, demographic disparities, and distributional shifts. Furthermore, we present an analytical model that provides insights into how training data selection contributes to the performance of generative models.

Good Data from Bad Models : Foundations of Threshold-based Auto-labeling

Creating large-scale high-quality labeled datasets is a major bottleneck in supervised machine learning workflows. Auto-labeling systems are a promising way to reduce reliance on manual labeling for dataset construction. Threshold-based auto-labeling, where validation data obtained from humans is used to find a threshold for confidence above which the data is machine-labeled, is emerging as a popular solution used widely in practice. Given the long shelf-life and diverse usage of the resulting datasets, understanding when the data obtained by such auto-labeling systems can be relied on is crucial. In this work, we analyze threshold-based auto-labeling systems and derive sample complexity bounds on the amount of human-labeled validation data required for guaranteeing the quality of machine-labeled data. Our results provide two insights. First, reasonable chunks of the unlabeled data can be automatically and accurately labeled by seemingly bad models. Second, a hidden downside of threshold-based auto-labeling systems is potentially prohibitive validation data usage. Together, these insights describe the promise and pitfalls of using such systems. We validate our theoretical guarantees with simulations and study the efficacy of threshold-based auto-labeling on real datasets.

One for All: Simultaneous Metric and Preference Learning over Multiple Users

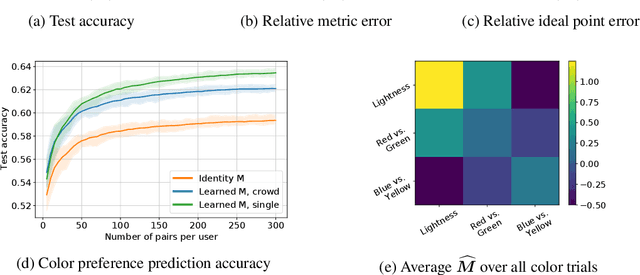
This paper investigates simultaneous preference and metric learning from a crowd of respondents. A set of items represented by $d$-dimensional feature vectors and paired comparisons of the form ``item $i$ is preferable to item $j$'' made by each user is given. Our model jointly learns a distance metric that characterizes the crowd's general measure of item similarities along with a latent ideal point for each user reflecting their individual preferences. This model has the flexibility to capture individual preferences, while enjoying a metric learning sample cost that is amortized over the crowd. We first study this problem in a noiseless, continuous response setting (i.e., responses equal to differences of item distances) to understand the fundamental limits of learning. Next, we establish prediction error guarantees for noisy, binary measurements such as may be collected from human respondents, and show how the sample complexity improves when the underlying metric is low-rank. Finally, we establish recovery guarantees under assumptions on the response distribution. We demonstrate the performance of our model on both simulated data and on a dataset of color preference judgements across a large number of users.

Fisher-Pitman permutation tests based on nonparametric Poisson mixtures with application to single cell genomics

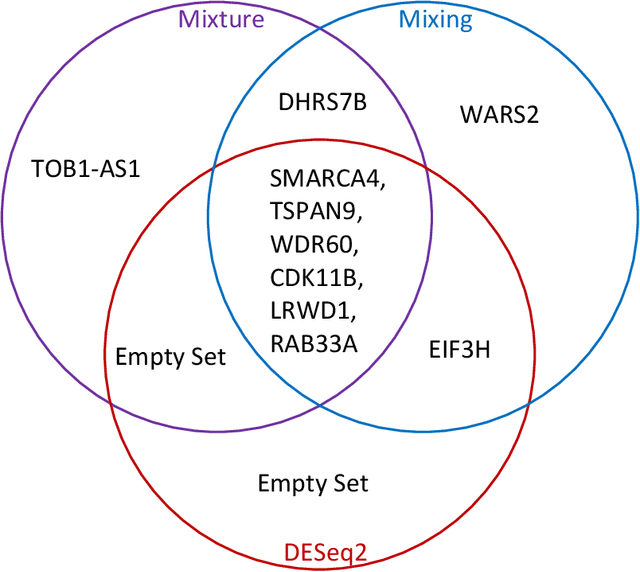
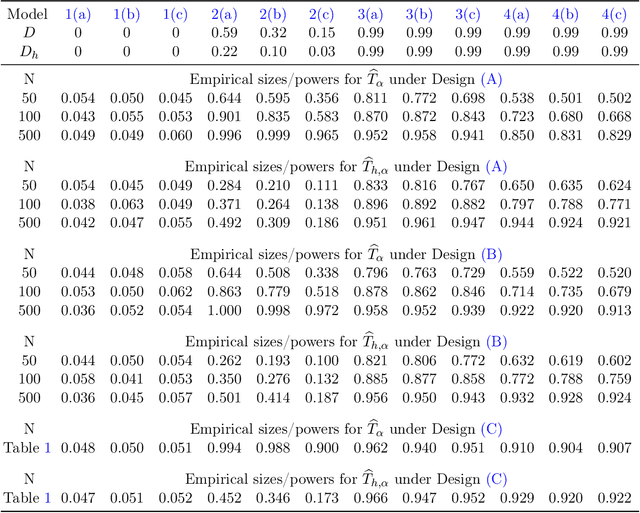
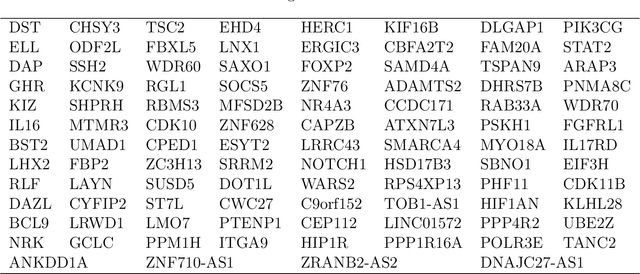
This paper investigates the theoretical and empirical performance of Fisher-Pitman-type permutation tests for assessing the equality of unknown Poisson mixture distributions. Building on nonparametric maximum likelihood estimators (NPMLEs) of the mixing distribution, these tests are theoretically shown to be able to adapt to complicated unspecified structures of count data and also consistent against their corresponding ANOVA-type alternatives; the latter is a result in parallel to classic claims made by Robinson (Robinson, 1973). The studied methods are then applied to a single-cell RNA-seq data obtained from different cell types from brain samples of autism subjects and healthy controls; empirically, they unveil genes that are differentially expressed between autism and control subjects yet are missed using common tests. For justifying their use, rate optimality of NPMLEs is also established in settings similar to nonparametric Gaussian (Wu and Yang, 2020a) and binomial mixtures (Tian et al., 2017; Vinayak et al., 2019).

Estimating the number and effect sizes of non-null hypotheses

We study the problem of estimating the distribution of effect sizes (the mean of the test statistic under the alternate hypothesis) in a multiple testing setting. Knowing this distribution allows us to calculate the power (type II error) of any experimental design. We show that it is possible to estimate this distribution using an inexpensive pilot experiment, which takes significantly fewer samples than would be required by an experiment that identified the discoveries. Our estimator can be used to guarantee the number of discoveries that will be made using a given experimental design in a future experiment. We prove that this simple and computationally efficient estimator enjoys a number of favorable theoretical properties, and demonstrate its effectiveness on data from a gene knockout experiment on influenza inhibition in Drosophila.

Optimal Estimation of Change in a Population of Parameters

Paired estimation of change in parameters of interest over a population plays a central role in several application domains including those in the social sciences, epidemiology, medicine and biology. In these domains, the size of the population under study is often very large, however, the number of observations available per individual in the population is very small (\emph{sparse observations}) which makes the problem challenging. Consider the setting with $N$ independent individuals, each with unknown parameters $(p_i, q_i)$ drawn from some unknown distribution on $[0, 1]^2$. We observe $X_i \sim \text{Bin}(t, p_i)$ before an event and $Y_i \sim \text{Bin}(t, q_i)$ after the event. Provided these paired observations, $\{(X_i, Y_i) \}_{i=1}^N$, our goal is to accurately estimate the \emph{distribution of the change in parameters}, $\delta_i := q_i - p_i$, over the population and properties of interest like the \emph{$\ell_1$-magnitude of the change} with sparse observations ($t\ll N$). We provide \emph{information theoretic lower bounds} on the error in estimating the distribution of change and the $\ell_1$-magnitude of change. Furthermore, we show that the following two step procedure achieves the optimal error bounds: first, estimate the full joint distribution of the paired parameters using the maximum likelihood estimator (MLE) and then estimate the distribution of change and the $\ell_1$-magnitude of change using the joint MLE. Notably, and perhaps surprisingly, these error bounds are of the same order as the minimax optimal error bounds for learning the \emph{full} joint distribution itself (in Wasserstein-1 distance); in other words, estimating the magnitude of the change of parameters over the population is, in a minimax sense, as difficult as estimating the full joint distribution itself.