Fang Han
Johns Hopkins University
Simultaneous Polysomnography and Cardiotocography Reveal Temporal Correlation Between Maternal Obstructive Sleep Apnea and Fetal Hypoxia
Apr 17, 2025Abstract:Background: Obstructive sleep apnea syndrome (OSAS) during pregnancy is common and can negatively affect fetal outcomes. However, studies on the immediate effects of maternal hypoxia on fetal heart rate (FHR) changes are lacking. Methods: We used time-synchronized polysomnography (PSG) and cardiotocography (CTG) data from two cohorts to analyze the correlation between maternal hypoxia and FHR changes (accelerations or decelerations). Maternal hypoxic event characteristics were analyzed using generalized linear modeling (GLM) to assess their associations with different FHR changes. Results: A total of 118 pregnant women participated. FHR changes were significantly associated with maternal hypoxia, primarily characterized by accelerations. A longer hypoxic duration correlated with more significant FHR accelerations (P < 0.05), while prolonged hypoxia and greater SpO2 drop were linked to FHR decelerations (P < 0.05). Both cohorts showed a transient increase in FHR during maternal hypoxia, which returned to baseline after the event resolved. Conclusion: Maternal hypoxia significantly affects FHR, suggesting that maternal OSAS may contribute to fetal hypoxia. These findings highlight the importance of maternal-fetal interactions and provide insights for future interventions.
STREAMLINE: An Automated Machine Learning Pipeline for Biomedicine Applied to Examine the Utility of Photography-Based Phenotypes for OSA Prediction Across International Sleep Centers
Dec 09, 2023



Abstract:While machine learning (ML) includes a valuable array of tools for analyzing biomedical data, significant time and expertise is required to assemble effective, rigorous, and unbiased pipelines. Automated ML (AutoML) tools seek to facilitate ML application by automating a subset of analysis pipeline elements. In this study we develop and validate a Simple, Transparent, End-to-end Automated Machine Learning Pipeline (STREAMLINE) and apply it to investigate the added utility of photography-based phenotypes for predicting obstructive sleep apnea (OSA); a common and underdiagnosed condition associated with a variety of health, economic, and safety consequences. STREAMLINE is designed to tackle biomedical binary classification tasks while adhering to best practices and accommodating complexity, scalability, reproducibility, customization, and model interpretation. Benchmarking analyses validated the efficacy of STREAMLINE across data simulations with increasingly complex patterns of association. Then we applied STREAMLINE to evaluate the utility of demographics (DEM), self-reported comorbidities (DX), symptoms (SYM), and photography-based craniofacial (CF) and intraoral (IO) anatomy measures in predicting any OSA or moderate/severe OSA using 3,111 participants from Sleep Apnea Global Interdisciplinary Consortium (SAGIC). OSA analyses identified a significant increase in ROC-AUC when adding CF to DEM+DX+SYM to predict moderate/severe OSA. A consistent but non-significant increase in PRC-AUC was observed with the addition of each subsequent feature set to predict any OSA, with CF and IO yielding minimal improvements. Application of STREAMLINE to OSA data suggests that CF features provide additional value in predicting moderate/severe OSA, but neither CF nor IO features meaningfully improved the prediction of any OSA beyond established demographics, comorbidity and symptom characteristics.
Limit theorems of Chatterjee's rank correlation
Apr 17, 2022Abstract:Establishing limiting distributions of Chatterjee's rank correlation for a general, possibly non-independent, pair of random variables has been eagerly awaited to many. This paper shows that (a) Chatterjee's rank correlation is asymptotically normal as long as one variable is not a measurable function of the other, and (b) the corresponding asymptotic variance is uniformly bounded by 36. Similar results also hold for Azadkia-Chatterjee's graph-based correlation coefficient, a multivariate analogue of Chatterjee's original proposal. The proof is given by appealing to H\'ajek representation and Chatterjee's nearest-neighbor CLT.
Nonparametric mixture MLEs under Gaussian-smoothed optimal transport distance
Dec 04, 2021Abstract:The Gaussian-smoothed optimal transport (GOT) framework, pioneered in Goldfeld et al. (2020) and followed up by a series of subsequent papers, has quickly caught attention among researchers in statistics, machine learning, information theory, and related fields. One key observation made therein is that, by adapting to the GOT framework instead of its unsmoothed counterpart, the curse of dimensionality for using the empirical measure to approximate the true data generating distribution can be lifted. The current paper shows that a related observation applies to the estimation of nonparametric mixing distributions in discrete exponential family models, where under the GOT cost the estimation accuracy of the nonparametric MLE can be accelerated to a polynomial rate. This is in sharp contrast to the classical sub-polynomial rates based on unsmoothed metrics, which cannot be improved from an information-theoretical perspective. A key step in our analysis is the establishment of a new Jackson-type approximation bound of Gaussian-convoluted Lipschitz functions. This insight bridges existing techniques of analyzing the nonparametric MLEs and the new GOT framework.
Fisher-Pitman permutation tests based on nonparametric Poisson mixtures with application to single cell genomics
Jun 06, 2021
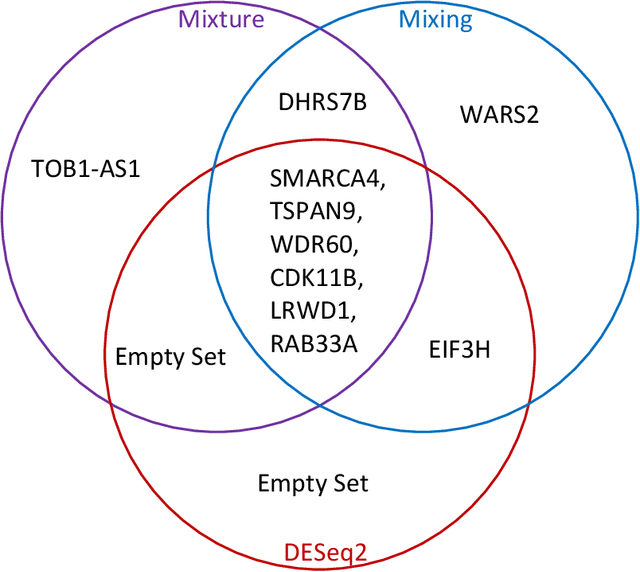
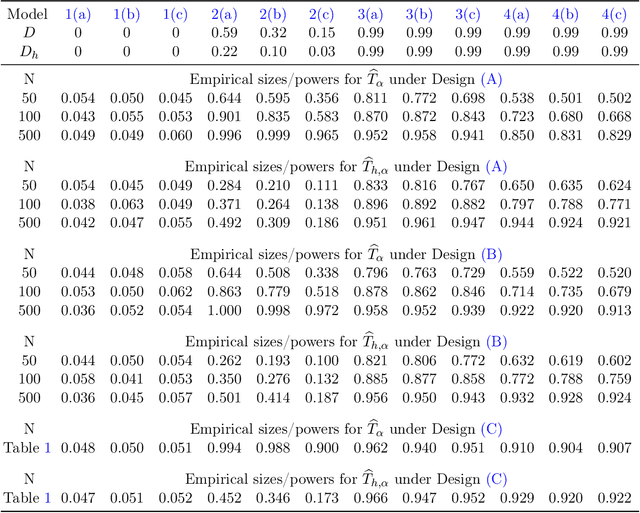
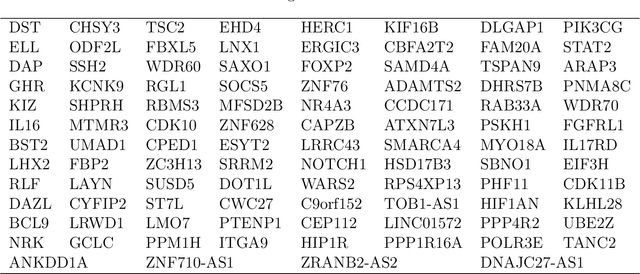
Abstract:This paper investigates the theoretical and empirical performance of Fisher-Pitman-type permutation tests for assessing the equality of unknown Poisson mixture distributions. Building on nonparametric maximum likelihood estimators (NPMLEs) of the mixing distribution, these tests are theoretically shown to be able to adapt to complicated unspecified structures of count data and also consistent against their corresponding ANOVA-type alternatives; the latter is a result in parallel to classic claims made by Robinson (Robinson, 1973). The studied methods are then applied to a single-cell RNA-seq data obtained from different cell types from brain samples of autism subjects and healthy controls; empirically, they unveil genes that are differentially expressed between autism and control subjects yet are missed using common tests. For justifying their use, rate optimality of NPMLEs is also established in settings similar to nonparametric Gaussian (Wu and Yang, 2020a) and binomial mixtures (Tian et al., 2017; Vinayak et al., 2019).
An Extreme-Value Approach for Testing the Equality of Large U-Statistic Based Correlation Matrices
Mar 30, 2018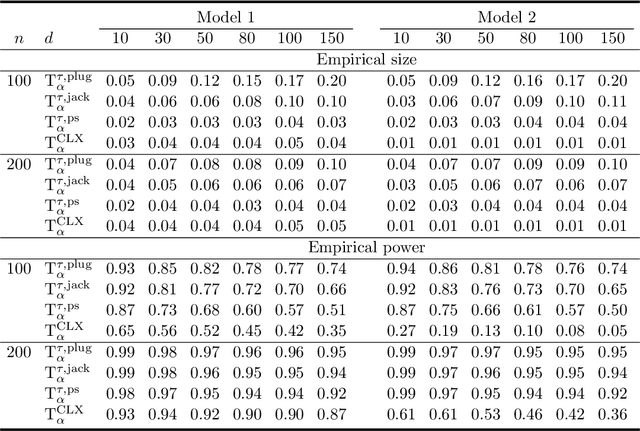
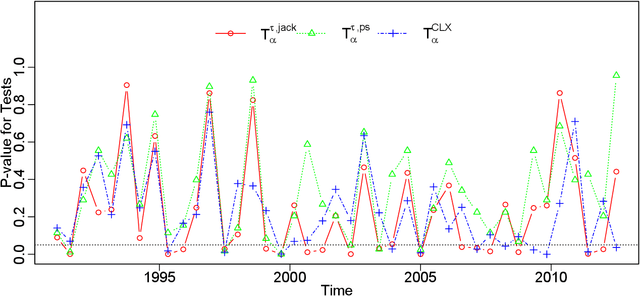
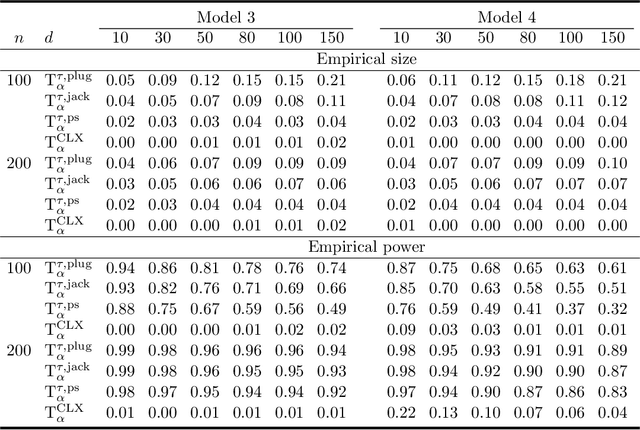
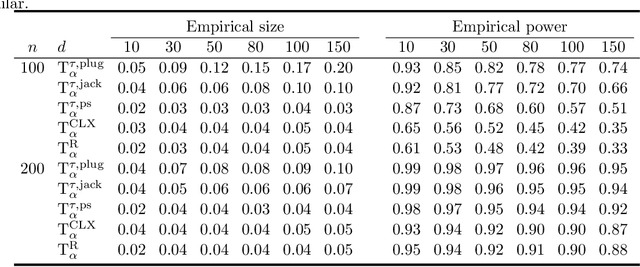
Abstract:There has been an increasing interest in testing the equality of large Pearson's correlation matrices. However, in many applications it is more important to test the equality of large rank-based correlation matrices since they are more robust to outliers and nonlinearity. Unlike the Pearson's case, testing the equality of large rank-based statistics has not been well explored and requires us to develop new methods and theory. In this paper, we provide a framework for testing the equality of two large U-statistic based correlation matrices, which include the rank-based correlation matrices as special cases. Our approach exploits extreme value statistics and the Jackknife estimator for uncertainty assessment and is valid under a fully nonparametric model. Theoretically, we develop a theory for testing the equality of U-statistic based correlation matrices. We then apply this theory to study the problem of testing large Kendall's tau correlation matrices and demonstrate its optimality. For proving this optimality, a novel construction of least favourable distributions is developed for the correlation matrix comparison.
ECA: High Dimensional Elliptical Component Analysis in non-Gaussian Distributions
Oct 03, 2016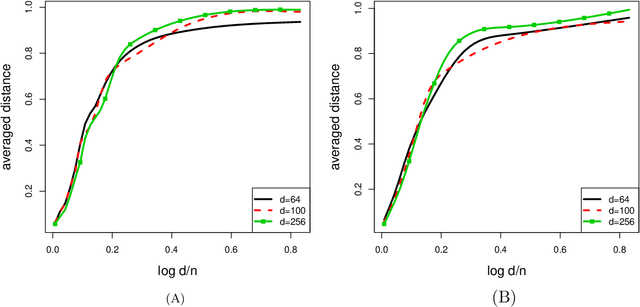

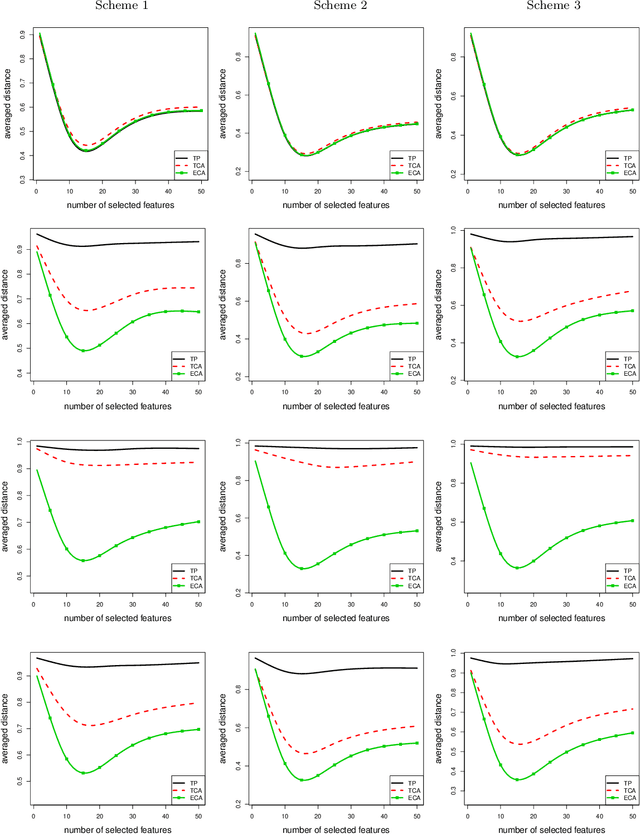
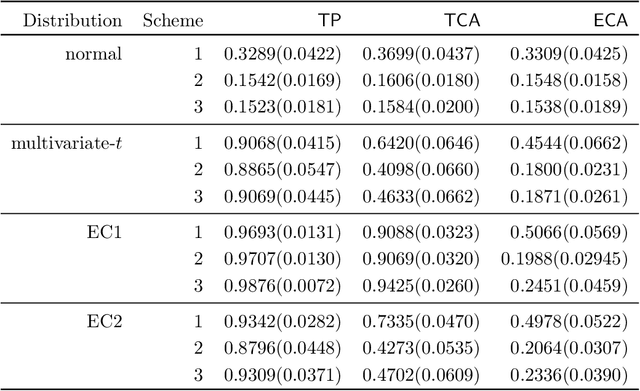
Abstract:We present a robust alternative to principal component analysis (PCA) --- called elliptical component analysis (ECA) --- for analyzing high dimensional, elliptically distributed data. ECA estimates the eigenspace of the covariance matrix of the elliptical data. To cope with heavy-tailed elliptical distributions, a multivariate rank statistic is exploited. At the model-level, we consider two settings: either that the leading eigenvectors of the covariance matrix are non-sparse or that they are sparse. Methodologically, we propose ECA procedures for both non-sparse and sparse settings. Theoretically, we provide both non-asymptotic and asymptotic analyses quantifying the theoretical performances of ECA. In the non-sparse setting, we show that ECA's performance is highly related to the effective rank of the covariance matrix. In the sparse setting, the results are twofold: (i) We show that the sparse ECA estimator based on a combinatoric program attains the optimal rate of convergence; (ii) Based on some recent developments in estimating sparse leading eigenvectors, we show that a computationally efficient sparse ECA estimator attains the optimal rate of convergence under a suboptimal scaling.
Statistical analysis of latent generalized correlation matrix estimation in transelliptical distribution
Sep 28, 2016Abstract:Correlation matrices play a key role in many multivariate methods (e.g., graphical model estimation and factor analysis). The current state-of-the-art in estimating large correlation matrices focuses on the use of Pearson's sample correlation matrix. Although Pearson's sample correlation matrix enjoys various good properties under Gaussian models, it is not an effective estimator when facing heavy-tailed distributions. As a robust alternative, Han and Liu [J. Am. Stat. Assoc. 109 (2015) 275-287] advocated the use of a transformed version of the Kendall's tau sample correlation matrix in estimating high dimensional latent generalized correlation matrix under the transelliptical distribution family (or elliptical copula). The transelliptical family assumes that after unspecified marginal monotone transformations, the data follow an elliptical distribution. In this paper, we study the theoretical properties of the Kendall's tau sample correlation matrix and its transformed version proposed in Han and Liu [J. Am. Stat. Assoc. 109 (2015) 275-287] for estimating the population Kendall's tau correlation matrix and the latent Pearson's correlation matrix under both spectral and restricted spectral norms. With regard to the spectral norm, we highlight the role of "effective rank" in quantifying the rate of convergence. With regard to the restricted spectral norm, we for the first time present a "sign sub-Gaussian condition" which is sufficient to guarantee that the rank-based correlation matrix estimator attains the fast rate of convergence. In both cases, we do not need any moment condition.
* Published at http://dx.doi.org/10.3150/15-BEJ702 in the Bernoulli (http://isi.cbs.nl/bernoulli/) by the International Statistical Institute/Bernoulli Society (http://isi.cbs.nl/BS/bshome.htm)
Challenges of Big Data Analysis
Dec 15, 2014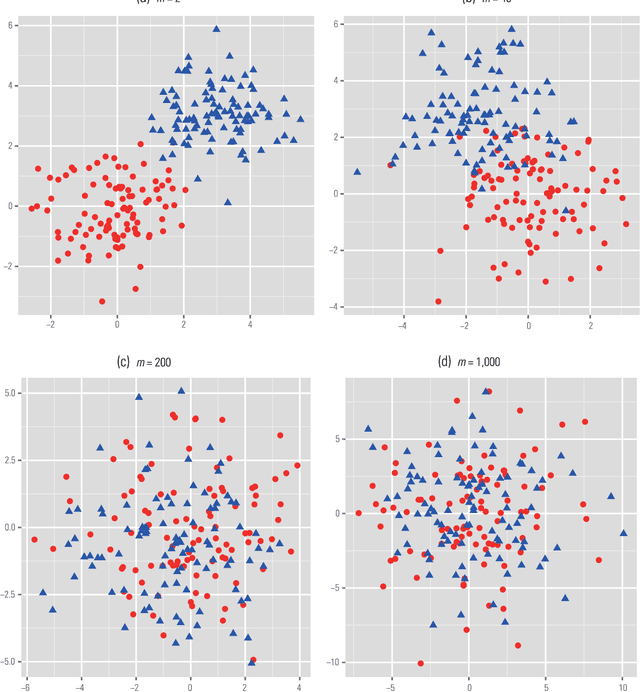
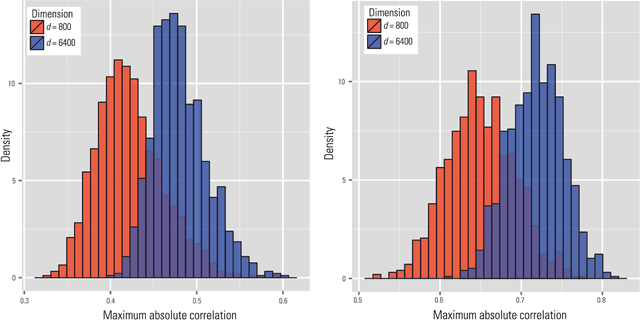
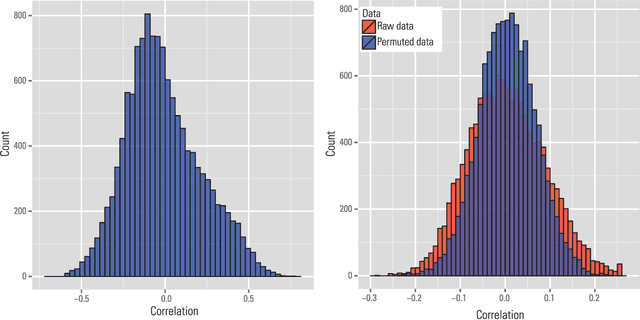
Abstract:Big Data bring new opportunities to modern society and challenges to data scientists. On one hand, Big Data hold great promises for discovering subtle population patterns and heterogeneities that are not possible with small-scale data. On the other hand, the massive sample size and high dimensionality of Big Data introduce unique computational and statistical challenges, including scalability and storage bottleneck, noise accumulation, spurious correlation, incidental endogeneity, and measurement errors. These challenges are distinguished and require new computational and statistical paradigm. This article give overviews on the salient features of Big Data and how these features impact on paradigm change on statistical and computational methods as well as computing architectures. We also provide various new perspectives on the Big Data analysis and computation. In particular, we emphasis on the viability of the sparsest solution in high-confidence set and point out that exogeneous assumptions in most statistical methods for Big Data can not be validated due to incidental endogeneity. They can lead to wrong statistical inferences and consequently wrong scientific conclusions.
A Direct Estimation of High Dimensional Stationary Vector Autoregressions
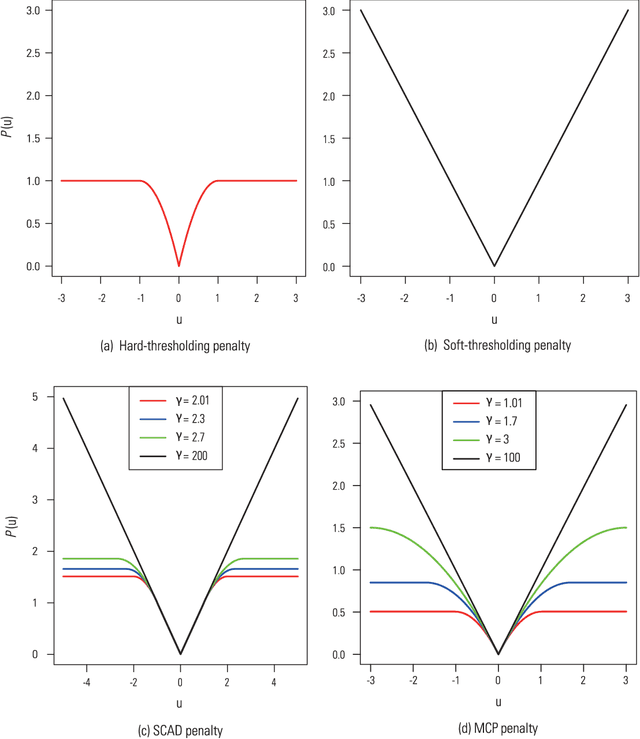
Oct 29, 2014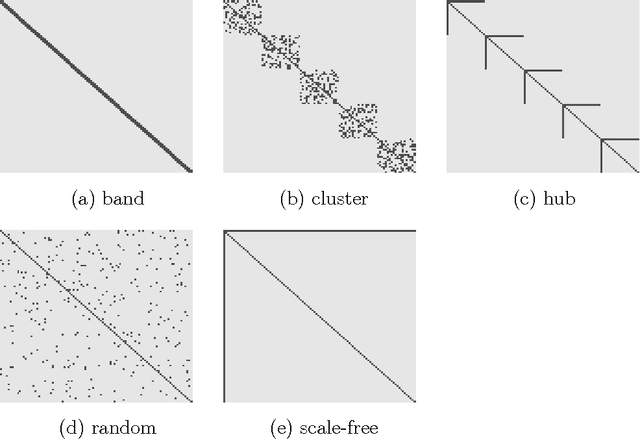
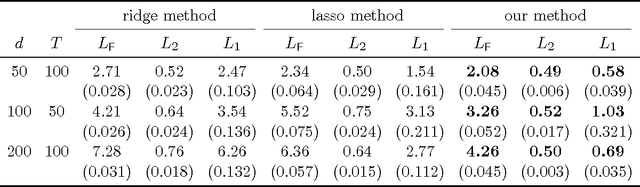
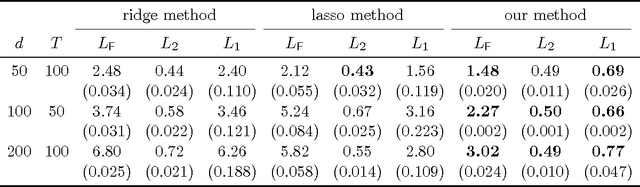
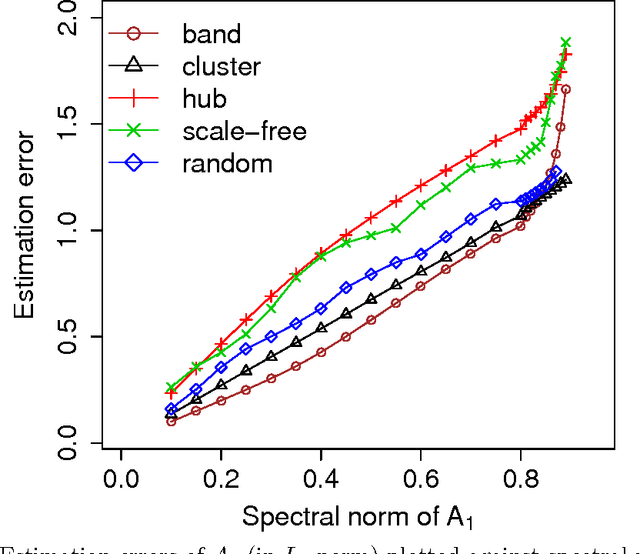
Abstract:The vector autoregressive (VAR) model is a powerful tool in modeling complex time series and has been exploited in many fields. However, fitting high dimensional VAR model poses some unique challenges: On one hand, the dimensionality, caused by modeling a large number of time series and higher order autoregressive processes, is usually much higher than the time series length; On the other hand, the temporal dependence structure in the VAR model gives rise to extra theoretical challenges. In high dimensions, one popular approach is to assume the transition matrix is sparse and fit the VAR model using the "least squares" method with a lasso-type penalty. In this manuscript, we propose an alternative way in estimating the VAR model. The main idea is, via exploiting the temporal dependence structure, to formulate the estimating problem into a linear program. There is instant advantage for the proposed approach over the lasso-type estimators: The estimation equation can be decomposed into multiple sub-equations and accordingly can be efficiently solved in a parallel fashion. In addition, our method brings new theoretical insights into the VAR model analysis. So far the theoretical results developed in high dimensions (e.g., Song and Bickel (2011) and Kock and Callot (2012)) mainly pose assumptions on the design matrix of the formulated regression problems. Such conditions are indirect about the transition matrices and not transparent. In contrast, our results show that the operator norm of the transition matrices plays an important role in estimation accuracy. We provide explicit rates of convergence for both estimation and prediction. In addition, we provide thorough experiments on both synthetic and real-world equity data to show that there are empirical advantages of our method over the lasso-type estimators in both parameter estimation and forecasting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge