Somdeb Sarkhel
GT-SVJ: Generative-Transformer-Based Self-Supervised Video Judge For Efficient Video Reward Modeling
Feb 05, 2026Abstract:Aligning video generative models with human preferences remains challenging: current approaches rely on Vision-Language Models (VLMs) for reward modeling, but these models struggle to capture subtle temporal dynamics. We propose a fundamentally different approach: repurposing video generative models, which are inherently designed to model temporal structure, as reward models. We present the Generative-Transformer-based Self-Supervised Video Judge (\modelname), a novel evaluation model that transforms state-of-the-art video generation models into powerful temporally-aware reward models. Our key insight is that generative models can be reformulated as energy-based models (EBMs) that assign low energy to high-quality videos and high energy to degraded ones, enabling them to discriminate video quality with remarkable precision when trained via contrastive objectives. To prevent the model from exploiting superficial differences between real and generated videos, we design challenging synthetic negative videos through controlled latent-space perturbations: temporal slicing, feature swapping, and frame shuffling, which simulate realistic but subtle visual degradations. This forces the model to learn meaningful spatiotemporal features rather than trivial artifacts. \modelname achieves state-of-the-art performance on GenAI-Bench and MonteBench using only 30K human-annotations: $6\times$ to $65\times$ fewer than existing VLM-based approaches.
Atom: Efficient On-Device Video-Language Pipelines Through Modular Reuse
Dec 18, 2025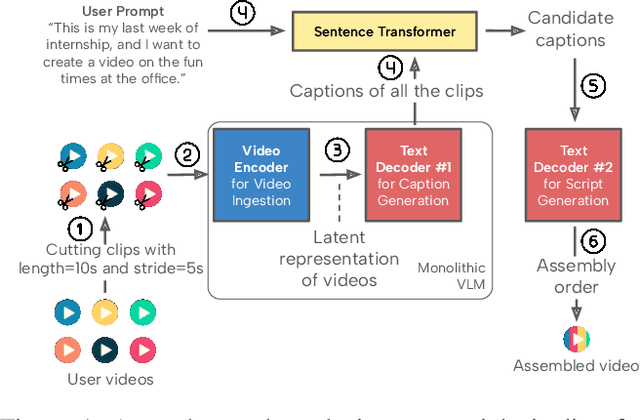

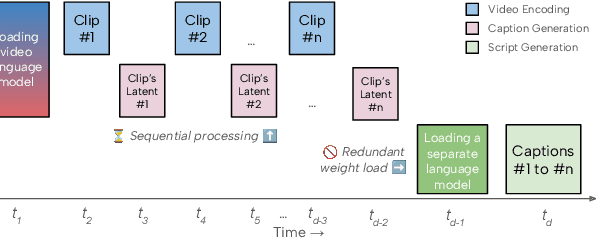

Abstract:Recent advances in video-language models have enabled powerful applications like video retrieval, captioning, and assembly. However, executing such multi-stage pipelines efficiently on mobile devices remains challenging due to redundant model loads and fragmented execution. We introduce Atom, an on-device system that restructures video-language pipelines for fast and efficient execution. Atom decomposes a billion-parameter model into reusable modules, such as the visual encoder and language decoder, and reuses them across subtasks like captioning, reasoning, and indexing. This reuse-centric design eliminates repeated model loading and enables parallel execution, reducing end-to-end latency without sacrificing performance. On commodity smartphones, Atom achieves 27--33% faster execution compared to non-reuse baselines, with only marginal performance drop ($\leq$ 2.3 Recall@1 in retrieval, $\leq$ 1.5 CIDEr in captioning). These results position Atom as a practical, scalable approach for efficient video-language understanding on edge devices.
Disentangling Fine-Tuning from Pre-Training in Visual Captioning with Hybrid Markov Logic
Mar 18, 2025Abstract:Multimodal systems have highly complex processing pipelines and are pretrained over large datasets before being fine-tuned for specific tasks such as visual captioning. However, it becomes hard to disentangle what the model learns during the fine-tuning process from what it already knows due to its pretraining. In this work, we learn a probabilistic model using Hybrid Markov Logic Networks (HMLNs) over the training examples by relating symbolic knowledge (extracted from the caption) with visual features (extracted from the image). For a generated caption, we quantify the influence of training examples based on the HMLN distribution using probabilistic inference. We evaluate two types of inference procedures on the MSCOCO dataset for different types of captioning models. Our results show that for BLIP2 (a model that uses a LLM), the fine-tuning may have smaller influence on the knowledge the model has acquired since it may have more general knowledge to perform visual captioning as compared to models that do not use a LLM
SKALD: Learning-Based Shot Assembly for Coherent Multi-Shot Video Creation
Mar 11, 2025
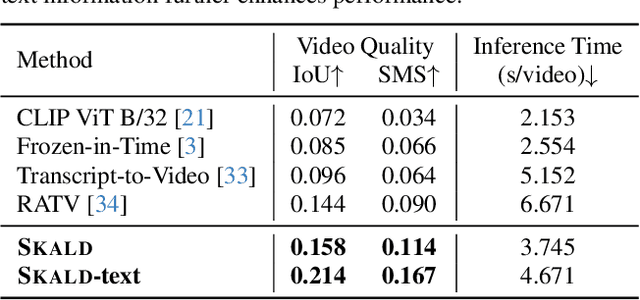

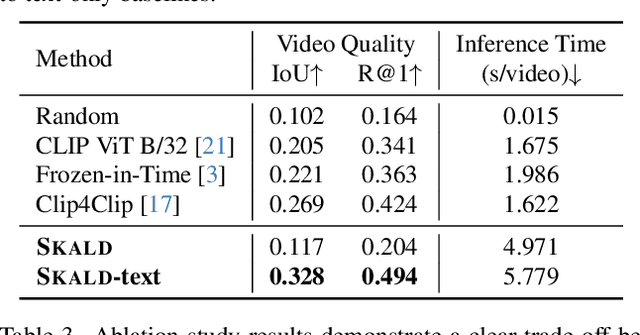
Abstract:We present SKALD, a multi-shot video assembly method that constructs coherent video sequences from candidate shots with minimal reliance on text. Central to our approach is the Learned Clip Assembly (LCA) score, a learning-based metric that measures temporal and semantic relationships between shots to quantify narrative coherence. We tackle the exponential complexity of combining multiple shots with an efficient beam-search algorithm guided by the LCA score. To train our model effectively with limited human annotations, we propose two tasks for the LCA encoder: Shot Coherence Learning, which uses contrastive learning to distinguish coherent and incoherent sequences, and Feature Regression, which converts these learned representations into a real-valued coherence score. We develop two variants: a base SKALD model that relies solely on visual coherence and SKALD-text, which integrates auxiliary text information when available. Experiments on the VSPD and our curated MSV3C datasets show that SKALD achieves an improvement of up to 48.6% in IoU and a 43% speedup over the state-of-the-art methods. A user study further validates our approach, with 45% of participants favoring SKALD-assembled videos, compared to 22% preferring text-based assembly methods.
X-Reflect: Cross-Reflection Prompting for Multimodal Recommendation
Aug 27, 2024



Abstract:Large Language Models (LLMs) and Large Multimodal Models (LMMs) have been shown to enhance the effectiveness of enriching item descriptions, thereby improving the accuracy of recommendation systems. However, most existing approaches either rely on text-only prompting or employ basic multimodal strategies that do not fully exploit the complementary information available from both textual and visual modalities. This paper introduces a novel framework, Cross-Reflection Prompting, termed X-Reflect, designed to address these limitations by prompting LMMs to explicitly identify and reconcile supportive and conflicting information between text and images. By capturing nuanced insights from both modalities, this approach generates more comprehensive and contextually richer item representations. Extensive experiments conducted on two widely used benchmarks demonstrate that our method outperforms existing prompting baselines in downstream recommendation accuracy. Additionally, we evaluate the generalizability of our framework across different LMM backbones and the robustness of the prompting strategies, offering insights for optimization. This work underscores the importance of integrating multimodal information and presents a novel solution for improving item understanding in multimodal recommendation systems.
Verifying Relational Explanations: A Probabilistic Approach
Jan 05, 2024Abstract:Explanations on relational data are hard to verify since the explanation structures are more complex (e.g. graphs). To verify interpretable explanations (e.g. explanations of predictions made in images, text, etc.), typically human subjects are used since it does not necessarily require a lot of expertise. However, to verify the quality of a relational explanation requires expertise and is hard to scale-up. GNNExplainer is arguably one of the most popular explanation methods for Graph Neural Networks. In this paper, we develop an approach where we assess the uncertainty in explanations generated by GNNExplainer. Specifically, we ask the explainer to generate explanations for several counterfactual examples. We generate these examples as symmetric approximations of the relational structure in the original data. From these explanations, we learn a factor graph model to quantify uncertainty in an explanation. Our results on several datasets show that our approach can help verify explanations from GNNExplainer by reliably estimating the uncertainty of a relation specified in the explanation.
On the verification of Embeddings using Hybrid Markov Logic
Dec 13, 2023



Abstract:The standard approach to verify representations learned by Deep Neural Networks is to use them in specific tasks such as classification or regression, and measure their performance based on accuracy in such tasks. However, in many cases, we would want to verify more complex properties of a learned representation. To do this, we propose a framework based on a probabilistic first-order language, namely, Hybrid Markov Logic Networks (HMLNs) where we specify properties over embeddings mixed with symbolic domain knowledge. We present an approach to learn parameters for the properties within this framework. Further, we develop a verification method to test embeddings in this framework by encoding this task as a Mixed Integer Linear Program for which we can leverage existing state-of-the-art solvers. We illustrate verification in Graph Neural Networks, Deep Knowledge Tracing and Intelligent Tutoring Systems to demonstrate the generality of our approach.
ToolChain*: Efficient Action Space Navigation in Large Language Models with A* Search
Oct 20, 2023



Abstract:Large language models (LLMs) have demonstrated powerful decision-making and planning capabilities in solving complicated real-world problems. LLM-based autonomous agents can interact with diverse tools (e.g., functional APIs) and generate solution plans that execute a series of API function calls in a step-by-step manner. The multitude of candidate API function calls significantly expands the action space, amplifying the critical need for efficient action space navigation. However, existing methods either struggle with unidirectional exploration in expansive action spaces, trapped into a locally optimal solution, or suffer from exhaustively traversing all potential actions, causing inefficient navigation. To address these issues, we propose ToolChain*, an efficient tree search-based planning algorithm for LLM-based agents. It formulates the entire action space as a decision tree, where each node represents a possible API function call involved in a solution plan. By incorporating the A* search algorithm with task-specific cost function design, it efficiently prunes high-cost branches that may involve incorrect actions, identifying the most low-cost valid path as the solution. Extensive experiments on multiple tool-use and reasoning tasks demonstrate that ToolChain* efficiently balances exploration and exploitation within an expansive action space. It outperforms state-of-the-art baselines on planning and reasoning tasks by 3.1% and 3.5% on average while requiring 7.35x and 2.31x less time, respectively.
A Faster $k$-means++ Algorithm
Nov 28, 2022



Abstract:K-means++ is an important algorithm to choose initial cluster centers for the k-means clustering algorithm. In this work, we present a new algorithm that can solve the $k$-means++ problem with near optimal running time. Given $n$ data points in $\mathbb{R}^d$, the current state-of-the-art algorithm runs in $\widetilde{O}(k )$ iterations, and each iteration takes $\widetilde{O}(nd k)$ time. The overall running time is thus $\widetilde{O}(n d k^2)$. We propose a new algorithm \textsc{FastKmeans++} that only takes in $\widetilde{O}(nd + nk^2)$ time, in total.
Optimal Bidding Strategy without Exploration in Real-time Bidding
Mar 31, 2020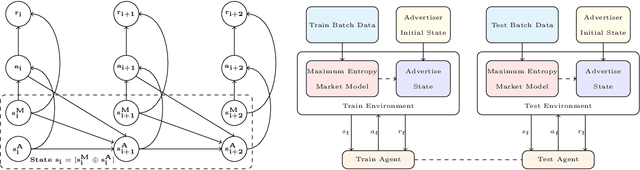
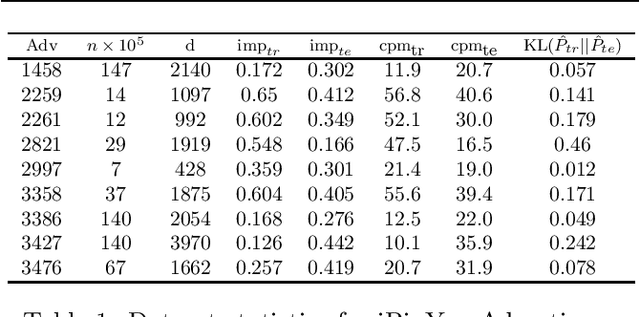
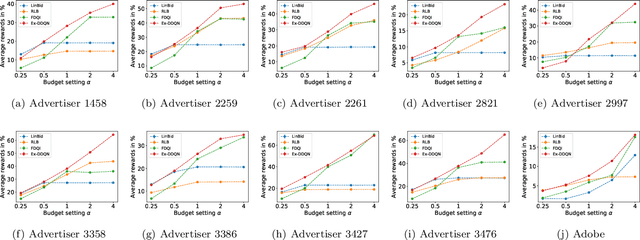
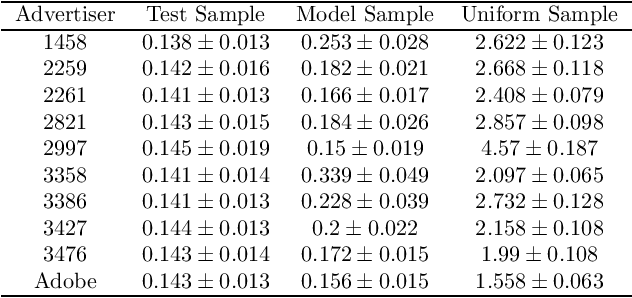
Abstract:Maximizing utility with a budget constraint is the primary goal for advertisers in real-time bidding (RTB) systems. The policy maximizing the utility is referred to as the optimal bidding strategy. Earlier works on optimal bidding strategy apply model-based batch reinforcement learning methods which can not generalize to unknown budget and time constraint. Further, the advertiser observes a censored market price which makes direct evaluation infeasible on batch test datasets. Previous works ignore the losing auctions to alleviate the difficulty with censored states; thus significantly modifying the test distribution. We address the challenge of lacking a clear evaluation procedure as well as the error propagated through batch reinforcement learning methods in RTB systems. We exploit two conditional independence structures in the sequential bidding process that allow us to propose a novel practical framework using the maximum entropy principle to imitate the behavior of the true distribution observed in real-time traffic. Moreover, the framework allows us to train a model that can generalize to the unseen budget conditions than limit only to those observed in history. We compare our methods on two real-world RTB datasets with several baselines and demonstrate significantly improved performance under various budget settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge