Discovering Data Structures: Nearest Neighbor Search and Beyond

We propose a general framework for end-to-end learning of data structures. Our framework adapts to the underlying data distribution and provides fine-grained control over query and space complexity. Crucially, the data structure is learned from scratch, and does not require careful initialization or seeding with candidate data structures/algorithms. We first apply this framework to the problem of nearest neighbor search. In several settings, we are able to reverse-engineer the learned data structures and query algorithms. For 1D nearest neighbor search, the model discovers optimal distribution (in)dependent algorithms such as binary search and variants of interpolation search. In higher dimensions, the model learns solutions that resemble k-d trees in some regimes, while in others, they have elements of locality-sensitive hashing. The model can also learn useful representations of high-dimensional data and exploit them to design effective data structures. We also adapt our framework to the problem of estimating frequencies over a data stream, and believe it could also be a powerful discovery tool for new problems.

Attribute-to-Delete: Machine Unlearning via Datamodel Matching

Machine unlearning -- efficiently removing the effect of a small "forget set" of training data on a pre-trained machine learning model -- has recently attracted significant research interest. Despite this interest, however, recent work shows that existing machine unlearning techniques do not hold up to thorough evaluation in non-convex settings. In this work, we introduce a new machine unlearning technique that exhibits strong empirical performance even in such challenging settings. Our starting point is the perspective that the goal of unlearning is to produce a model whose outputs are statistically indistinguishable from those of a model re-trained on all but the forget set. This perspective naturally suggests a reduction from the unlearning problem to that of data attribution, where the goal is to predict the effect of changing the training set on a model's outputs. Thus motivated, we propose the following meta-algorithm, which we call Datamodel Matching (DMM): given a trained model, we (a) use data attribution to predict the output of the model if it were re-trained on all but the forget set points; then (b) fine-tune the pre-trained model to match these predicted outputs. In a simple convex setting, we show how this approach provably outperforms a variety of iterative unlearning algorithms. Empirically, we use a combination of existing evaluations and a new metric based on the KL-divergence to show that even in non-convex settings, DMM achieves strong unlearning performance relative to existing algorithms. An added benefit of DMM is that it is a meta-algorithm, in the sense that future advances in data attribution translate directly into better unlearning algorithms, pointing to a clear direction for future progress in unlearning.

Pipe Routing with Topology Control for UAV Networks

Routing protocols help in transmitting the sensed data from UAVs monitoring the targets (called target UAVs) to the BS. However, the highly dynamic nature of an autonomous, decentralized UAV network leads to frequent route breaks or traffic disruptions. Traditional routing schemes cannot quickly adapt to dynamic UAV networks and/or incur large control overhead and delays. To establish stable, high-quality routes from target UAVs to the BS, we design a hybrid reactive routing scheme called pipe routing that is mobility, congestion, and energy-aware. The pipe routing scheme discovers routes on-demand and proactively switches to alternate high-quality routes within a limited region around the active routes (called the pipe) when needed, reducing the number of route breaks and increasing data throughput. We then design a novel topology control-based pipe routing scheme to maintain robust connectivity in the pipe region around the active routes, leading to improved route stability and increased throughput with minimal impact on the coverage performance of the UAV network.

Testing with Non-identically Distributed Samples

We examine the extent to which sublinear-sample property testing and estimation applies to settings where samples are independently but not identically distributed. Specifically, we consider the following distributional property testing framework: Suppose there is a set of distributions over a discrete support of size $k$, $\textbf{p}_1, \textbf{p}_2,\ldots,\textbf{p}_T$, and we obtain $c$ independent draws from each distribution. Suppose the goal is to learn or test a property of the average distribution, $\textbf{p}_{\mathrm{avg}}$. This setup models a number of important practical settings where the individual distributions correspond to heterogeneous entities -- either individuals, chronologically distinct time periods, spatially separated data sources, etc. From a learning standpoint, even with $c=1$ samples from each distribution, $\Theta(k/\varepsilon^2)$ samples are necessary and sufficient to learn $\textbf{p}_{\mathrm{avg}}$ to within error $\varepsilon$ in TV distance. To test uniformity or identity -- distinguishing the case that $\textbf{p}_{\mathrm{avg}}$ is equal to some reference distribution, versus has $\ell_1$ distance at least $\varepsilon$ from the reference distribution, we show that a linear number of samples in $k$ is necessary given $c=1$ samples from each distribution. In contrast, for $c \ge 2$, we recover the usual sublinear sample testing of the i.i.d. setting: we show that $O(\sqrt{k}/\varepsilon^2 + 1/\varepsilon^4)$ samples are sufficient, matching the optimal sample complexity in the i.i.d. case in the regime where $\varepsilon \ge k^{-1/4}$. Additionally, we show that in the $c=2$ case, there is a constant $\rho > 0$ such that even in the linear regime with $\rho k$ samples, no tester that considers the multiset of samples (ignoring which samples were drawn from the same $\textbf{p}_i$) can perform uniformity testing.

What Can Transformers Learn In-Context? A Case Study of Simple Function Classes

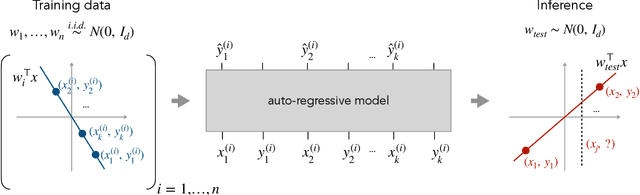
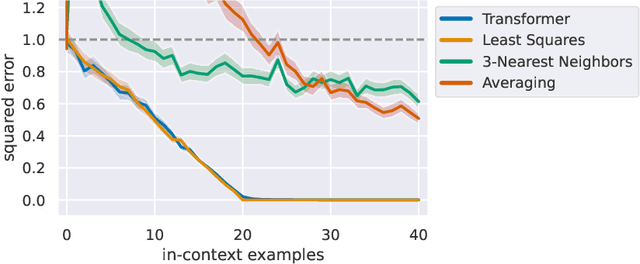
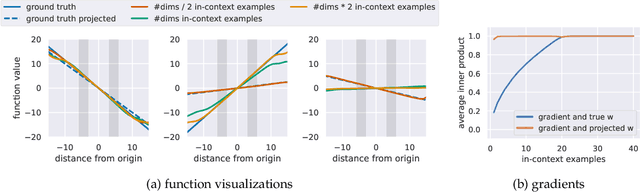
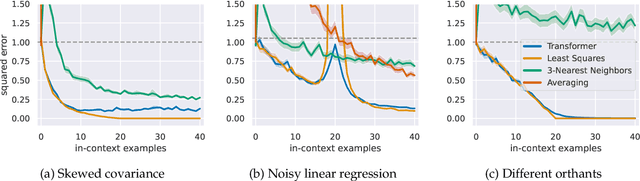
In-context learning refers to the ability of a model to condition on a prompt sequence consisting of in-context examples (input-output pairs corresponding to some task) along with a new query input, and generate the corresponding output. Crucially, in-context learning happens only at inference time without any parameter updates to the model. While large language models such as GPT-3 exhibit some ability to perform in-context learning, it is unclear what the relationship is between tasks on which this succeeds and what is present in the training data. To make progress towards understanding in-context learning, we consider the well-defined problem of training a model to in-context learn a function class (e.g., linear functions): that is, given data derived from some functions in the class, can we train a model to in-context learn "most" functions from this class? We show empirically that standard Transformers can be trained from scratch to perform in-context learning of linear functions -- that is, the trained model is able to learn unseen linear functions from in-context examples with performance comparable to the optimal least squares estimator. In fact, in-context learning is possible even under two forms of distribution shift: (i) between the training data of the model and inference-time prompts, and (ii) between the in-context examples and the query input during inference. We also show that we can train Transformers to in-context learn more complex function classes -- namely sparse linear functions, two-layer neural networks, and decision trees -- with performance that matches or exceeds task-specific learning algorithms. Our code and models are available at https://github.com/dtsip/in-context-learning .

Accurate Link Lifetime Computation in Autonomous Airborne UAV Networks

An autonomous airborne network (AN) consists of multiple unmanned aerial vehicles (UAVs), which can self-configure to provide seamless, low-cost and secure connectivity. AN is preferred for applications in civilian and military sectors because it can improve the network reliability and fault tolerance, reduce mission completion time through collaboration, and adapt to dynamic mission requirements. However, facilitating seamless communication in such ANs is a challenging task due to their fast node mobility, which results in frequent link disruptions. Many existing AN-specific mobility-aware schemes restrictively assume that UAVs fly in straight lines, to reduce the high uncertainty in the mobility pattern and simplify the calculation of link lifetime (LLT). Here, LLT represents the duration after which the link between a node pair terminates. However, the application of such schemes is severely limited, which makes them unsuitable for practical autonomous ANs. In this report, a mathematical framework is described to accurately compute the \textit{LLT} value for a UAV node pair, where each node flies independently in a randomly selected smooth trajectory. In addition, the impact of random trajectory changes on LLT accuracy is also discussed.

On the Statistical Complexity of Sample Amplification

Given $n$ i.i.d. samples drawn from an unknown distribution $P$, when is it possible to produce a larger set of $n+m$ samples which cannot be distinguished from $n+m$ i.i.d. samples drawn from $P$? (Axelrod et al. 2019) formalized this question as the sample amplification problem, and gave optimal amplification procedures for discrete distributions and Gaussian location models. However, these procedures and associated lower bounds are tailored to the specific distribution classes, and a general statistical understanding of sample amplification is still largely missing. In this work, we place the sample amplification problem on a firm statistical foundation by deriving generally applicable amplification procedures, lower bound techniques and connections to existing statistical notions. Our techniques apply to a large class of distributions including the exponential family, and establish a rigorous connection between sample amplification and distribution learning.

An Alternate Policy Gradient Estimator for Softmax Policies

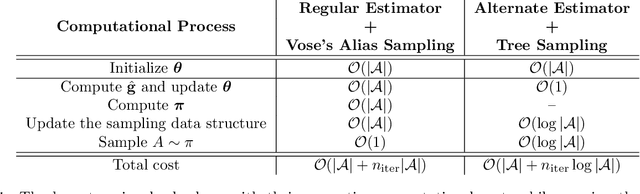
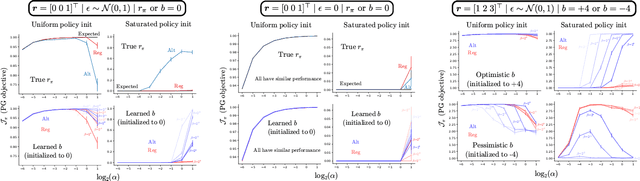
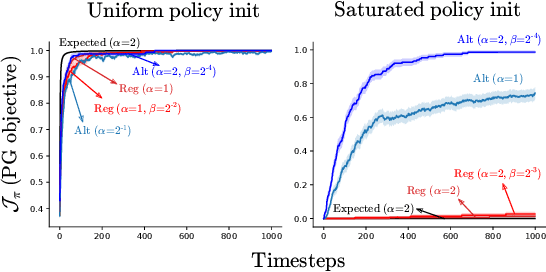
Policy gradient (PG) estimators for softmax policies are ineffective with sub-optimally saturated initialization, which happens when the density concentrates on a sub-optimal action. Sub-optimal policy saturation may arise from bad policy initialization or sudden changes in the environment that occur after the policy has already converged, and softmax PG estimators require a large number of updates to recover an effective policy. This severe issue causes high sample inefficiency and poor adaptability to new situations. To mitigate this problem, we propose a novel policy gradient estimator for softmax policies that utilizes the bias in the critic estimate and the noise present in the reward signal to escape the saturated regions of the policy parameter space. Our analysis and experiments, conducted on bandits and classical MDP benchmarking tasks, show that our estimator is more robust to policy saturation.

How and When Random Feedback Works: A Case Study of Low-Rank Matrix Factorization

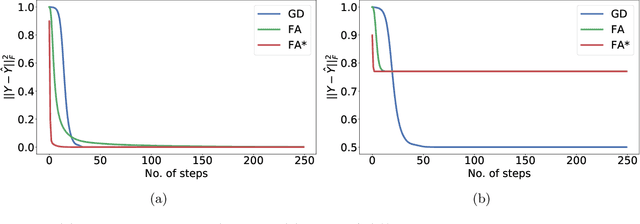
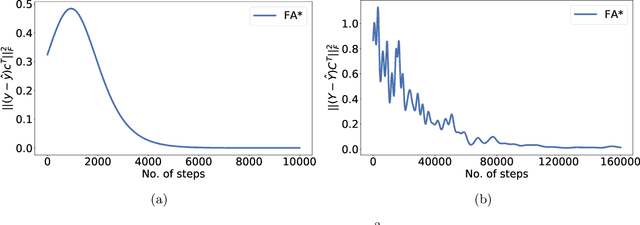
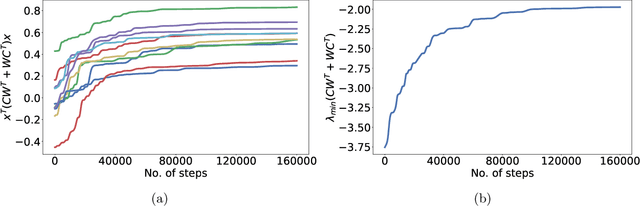
The success of gradient descent in ML and especially for learning neural networks is remarkable and robust. In the context of how the brain learns, one aspect of gradient descent that appears biologically difficult to realize (if not implausible) is that its updates rely on feedback from later layers to earlier layers through the same connections. Such bidirected links are relatively few in brain networks, and even when reciprocal connections exist, they may not be equi-weighted. Random Feedback Alignment (Lillicrap et al., 2016), where the backward weights are random and fixed, has been proposed as a bio-plausible alternative and found to be effective empirically. We investigate how and when feedback alignment (FA) works, focusing on one of the most basic problems with layered structure -- low-rank matrix factorization. In this problem, given a matrix $Y_{n\times m}$, the goal is to find a low rank factorization $Z_{n \times r}W_{r \times m}$ that minimizes the error $\|ZW-Y\|_F$. Gradient descent solves this problem optimally. We show that FA converges to the optimal solution when $r\ge \mbox{rank}(Y)$. We also shed light on how FA works. It is observed empirically that the forward weight matrices and (random) feedback matrices come closer during FA updates. Our analysis rigorously derives this phenomenon and shows how it facilitates convergence of FA. We also show that FA can be far from optimal when $r < \mbox{rank}(Y)$. This is the first provable separation result between gradient descent and FA. Moreover, the representations found by gradient descent and FA can be almost orthogonal even when their error $\|ZW-Y\|_F$ is approximately equal.

Gradient Temporal-Difference Learning with Regularized Corrections

It is still common to use Q-learning and temporal difference (TD) learning-even though they have divergence issues and sound Gradient TD alternatives exist-because divergence seems rare and they typically perform well. However, recent work with large neural network learning systems reveals that instability is more common than previously thought. Practitioners face a difficult dilemma: choose an easy to use and performant TD method, or a more complex algorithm that is more sound but harder to tune and all but unexplored with non-linear function approximation or control. In this paper, we introduce a new method called TD with Regularized Corrections (TDRC), that attempts to balance ease of use, soundness, and performance. It behaves as well as TD, when TD performs well, but is sound in cases where TD diverges. We empirically investigate TDRC across a range of problems, for both prediction and control, and for both linear and non-linear function approximation, and show, potentially for the first time, that gradient TD methods could be a better alternative to TD and Q-learning.