LieRE: Generalizing Rotary Position Encodings

While Rotary Position Embeddings (RoPE) for natural language performs well and has become widely adopted, its adoption for other modalities has been slower. Here, we introduce Lie group Relative position Encodings (LieRE) that goes beyond RoPE in supporting higher dimensional inputs. We evaluate the performance of LieRE on 2D and 3D image classification tasks and observe that LieRE leads to marked improvements in performance (up to 6%), training efficiency (3.5x reduction), data efficiency (30%) compared to the baselines of RoFormer, DeiT III, RoPE-Mixed and Vision-Llama

Random Expert Sampling for Deep Learning Segmentation of Acute Ischemic Stroke on Non-contrast CT

Purpose: Multi-expert deep learning training methods to automatically quantify ischemic brain tissue on Non-Contrast CT Materials and Methods: The data set consisted of 260 Non-Contrast CTs from 233 patients of acute ischemic stroke patients recruited in the DEFUSE 3 trial. A benchmark U-Net was trained on the reference annotations of three experienced neuroradiologists to segment ischemic brain tissue using majority vote and random expert sampling training schemes. We used a one-sided Wilcoxon signed-rank test on a set of segmentation metrics to compare bootstrapped point estimates of the training schemes with the inter-expert agreement and ratio of variance for consistency analysis. We further compare volumes with the 24h-follow-up DWI (final infarct core) in the patient subgroup with full reperfusion and we test volumes for correlation to the clinical outcome (mRS after 30 and 90 days) with the Spearman method. Results: Random expert sampling leads to a model that shows better agreement with experts than experts agree among themselves and better agreement than the agreement between experts and a majority-vote model performance (Surface Dice at Tolerance 5mm improvement of 61% to 0.70 +- 0.03 and Dice improvement of 25% to 0.50 +- 0.04). The model-based predicted volume similarly estimated the final infarct volume and correlated better to the clinical outcome than CT perfusion. Conclusion: A model trained on random expert sampling can identify the presence and location of acute ischemic brain tissue on Non-Contrast CT similar to CT perfusion and with better consistency than experts. This may further secure the selection of patients eligible for endovascular treatment in less specialized hospitals.

Non-inferiority of Deep Learning Model to Segment Acute Stroke on Non-contrast CT Compared to Neuroradiologists

Purpose: To develop a deep learning model to segment the acute ischemic infarct on non-contrast Computed Tomography (NCCT). Materials and Methods In this retrospective study, 227 Head NCCT examinations from 200 patients enrolled in the multicenter DEFUSE 3 trial were included. Three experienced neuroradiologists (experts A, B and C) independently segmented the acute infarct on each study. The dataset was randomly split into 5 folds with training and validation cases. A 3D deep Convolutional Neural Network (CNN) architecture was optimized for the data set properties and task needs. The input to the model was the NCCT and the output was a segmentation mask. The model was trained and optimized on expert A. The outcome was assessed by a set of volume, overlap and distance metrics. The predicted segmentations of the best model and expert A were compared to experts B and C. Then we used a paired Wilcoxon signed-rank test in a one-sided test procedure for all metrics to test for non-inferiority in terms of bias and precision. Results: The best performing model reached a Surface Dice at Tolerance (SDT)5mm of 0.68 \pm 0.04. The predictions were non-inferior when compared to independent experts in terms of bias and precision (paired one-sided test procedure for differences in medians and bootstrapped standard deviations with non-inferior boundaries of -0.05, 2ml, and 2mm, p < 0.05, n=200). Conclusion: For the segmentation of acute ischemic stroke on NCCT, our 3D CNN trained with the annotations of one neuroradiologist is non-inferior when compared to two independent neuroradiologists.

Evaluation of Medical Image Segmentation Models for Uncertain, Small or Empty Reference Annotations

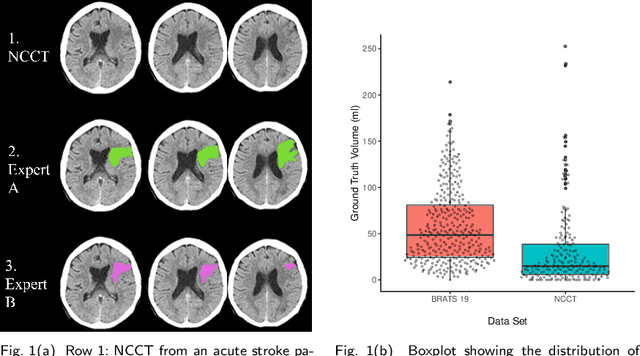
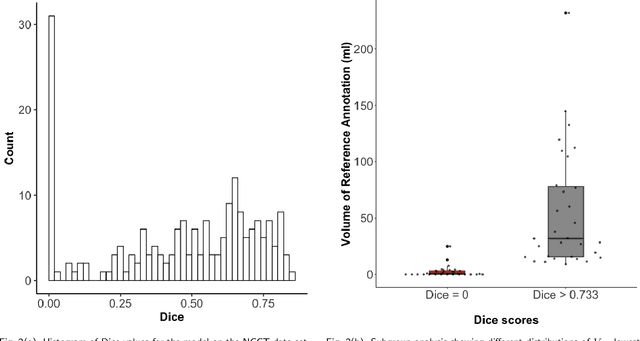
Performance metrics for medical image segmentation models are used to measure agreement between the reference annotation and the prediction. A common set of metrics is used in the development of such models to make results more comparable. However, there is a mismatch between the distributions in public data sets and cases encountered in clinical practice. Many common metrics fail to measure the impact of this mismatch, especially for clinical data sets containing uncertain, small or empty reference annotation. Thus, models may not be validated for clinically meaningful agreement by such metrics. Dimensions of evaluating clinical value include independence from reference annotation volume size, consideration of uncertainty of reference annotations, reward of volumetric and/or location agreement and reward of correct classification of empty reference annotations. Unlike common public data sets, our in-house data set is more representative. It contains uncertain, small or empty reference annotations. We examine publicly available metrics on the predictions of a deep learning framework in order to identify for which settings common metrics provide clinical meaningful results. We compare to a public benchmark data set without uncertain, small or empty reference annotations. https://github.com/SophieOstmeier/UncertainSmallEmpty

On the Statistical Complexity of Sample Amplification

Given $n$ i.i.d. samples drawn from an unknown distribution $P$, when is it possible to produce a larger set of $n+m$ samples which cannot be distinguished from $n+m$ i.i.d. samples drawn from $P$? (Axelrod et al. 2019) formalized this question as the sample amplification problem, and gave optimal amplification procedures for discrete distributions and Gaussian location models. However, these procedures and associated lower bounds are tailored to the specific distribution classes, and a general statistical understanding of sample amplification is still largely missing. In this work, we place the sample amplification problem on a firm statistical foundation by deriving generally applicable amplification procedures, lower bound techniques and connections to existing statistical notions. Our techniques apply to a large class of distributions including the exponential family, and establish a rigorous connection between sample amplification and distribution learning.

Learning From Strategic Agents: Accuracy, Improvement, and Causality

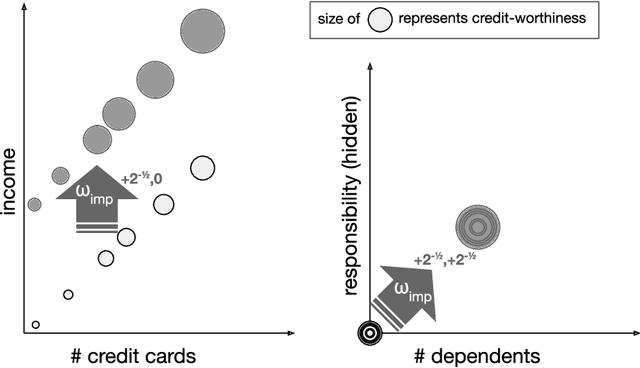
In many predictive decision-making scenarios, such as credit scoring and academic testing, a decision-maker must construct a model (predicting some outcome) that accounts for agents' incentives to "game" their features in order to receive better decisions. Whereas the strategic classification literature generally assumes that agents' outcomes are not causally dependent on their features (and thus strategic behavior is a form of lying), we join concurrent work in modeling agents' outcomes as a function of their changeable attributes. Our formulation is the first to incorporate a crucial phenomenon: when agents act to change observable features, they may as a side effect perturb hidden features that causally affect their true outcomes. We consider three distinct desiderata for a decision-maker's model: accurately predicting agents' post-gaming outcomes (accuracy), incentivizing agents to improve these outcomes (improvement), and, in the linear setting, estimating the visible coefficients of the true causal model (causal precision). As our main contribution, we provide the first algorithms for learning accuracy-optimizing, improvement-optimizing, and causal-precision-optimizing linear regression models directly from data, without prior knowledge of agents' possible actions. These algorithms circumvent the hardness result of Miller et al. (2019) by allowing the decision maker to observe agents' responses to a sequence of decision rules, in effect inducing agents to perform causal interventions for free.

Sample Amplification: Increasing Dataset Size even when Learning is Impossible

Given data drawn from an unknown distribution, $D$, to what extent is it possible to ``amplify'' this dataset and output an even larger set of samples that appear to have been drawn from $D$? We formalize this question as follows: an $(n,m)$ $\text{amplification procedure}$ takes as input $n$ independent draws from an unknown distribution $D$, and outputs a set of $m > n$ ``samples''. An amplification procedure is valid if no algorithm can distinguish the set of $m$ samples produced by the amplifier from a set of $m$ independent draws from $D$, with probability greater than $2/3$. Perhaps surprisingly, in many settings, a valid amplification procedure exists, even when the size of the input dataset, $n$, is significantly less than what would be necessary to learn $D$ to non-trivial accuracy. Specifically we consider two fundamental settings: the case where $D$ is an arbitrary discrete distribution supported on $\le k$ elements, and the case where $D$ is a $d$-dimensional Gaussian with unknown mean, and fixed covariance. In the first case, we show that an $\left(n, n + \Theta(\frac{n}{\sqrt{k}})\right)$ amplifier exists. In particular, given $n=O(\sqrt{k})$ samples from $D$, one can output a set of $m=n+1$ datapoints, whose total variation distance from the distribution of $m$ i.i.d. draws from $D$ is a small constant, despite the fact that one would need quadratically more data, $n=\Theta(k)$, to learn $D$ up to small constant total variation distance. In the Gaussian case, we show that an $\left(n,n+\Theta(\frac{n}{\sqrt{d}} )\right)$ amplifier exists, even though learning the distribution to small constant total variation distance requires $\Theta(d)$ samples. In both the discrete and Gaussian settings, we show that these results are tight, to constant factors. Beyond these results, we formalize a number of curious directions for future research along this vein.

Provably Safe Robot Navigation with Obstacle Uncertainty

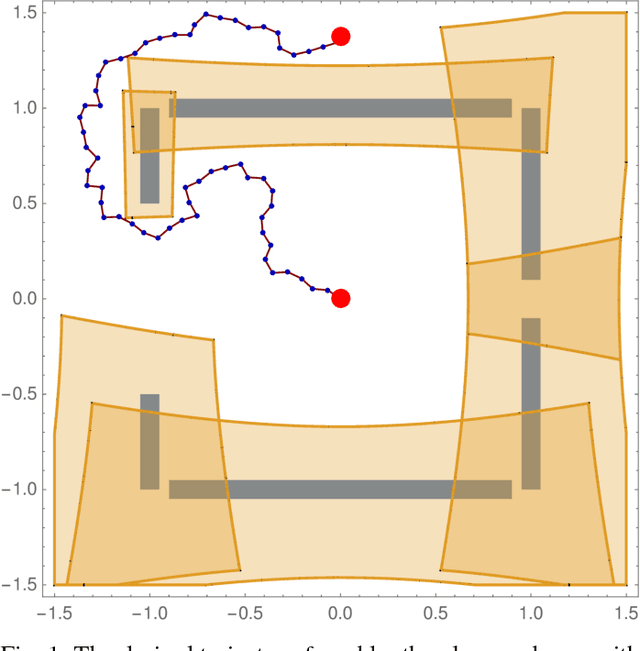
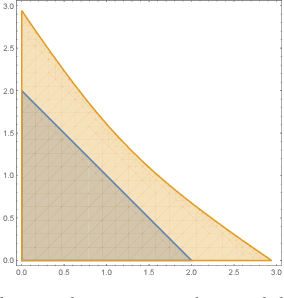
As drones and autonomous cars become more widespread it is becoming increasingly important that robots can operate safely under realistic conditions. The noisy information fed into real systems means that robots must use estimates of the environment to plan navigation. Efficiently guaranteeing that the resulting motion plans are safe under these circumstances has proved difficult. We examine how to guarantee that a trajectory or policy is safe with only imperfect observations of the environment. We examine the implications of various mathematical formalisms of safety and arrive at a mathematical notion of safety of a long-term execution, even when conditioned on observational information. We present efficient algorithms that can prove that trajectories or policies are safe with much tighter bounds than in previous work. Notably, the complexity of the environment does not affect our methods ability to evaluate if a trajectory or policy is safe. We then use these safety checking methods to design a safe variant of the RRT planning algorithm.