Attribute-to-Delete: Machine Unlearning via Datamodel Matching

Machine unlearning -- efficiently removing the effect of a small "forget set" of training data on a pre-trained machine learning model -- has recently attracted significant research interest. Despite this interest, however, recent work shows that existing machine unlearning techniques do not hold up to thorough evaluation in non-convex settings. In this work, we introduce a new machine unlearning technique that exhibits strong empirical performance even in such challenging settings. Our starting point is the perspective that the goal of unlearning is to produce a model whose outputs are statistically indistinguishable from those of a model re-trained on all but the forget set. This perspective naturally suggests a reduction from the unlearning problem to that of data attribution, where the goal is to predict the effect of changing the training set on a model's outputs. Thus motivated, we propose the following meta-algorithm, which we call Datamodel Matching (DMM): given a trained model, we (a) use data attribution to predict the output of the model if it were re-trained on all but the forget set points; then (b) fine-tune the pre-trained model to match these predicted outputs. In a simple convex setting, we show how this approach provably outperforms a variety of iterative unlearning algorithms. Empirically, we use a combination of existing evaluations and a new metric based on the KL-divergence to show that even in non-convex settings, DMM achieves strong unlearning performance relative to existing algorithms. An added benefit of DMM is that it is a meta-algorithm, in the sense that future advances in data attribution translate directly into better unlearning algorithms, pointing to a clear direction for future progress in unlearning.

ContextCite: Attributing Model Generation to Context

How do language models use information provided as context when generating a response? Can we infer whether a particular generated statement is actually grounded in the context, a misinterpretation, or fabricated? To help answer these questions, we introduce the problem of context attribution: pinpointing the parts of the context (if any) that led a model to generate a particular statement. We then present ContextCite, a simple and scalable method for context attribution that can be applied on top of any existing language model. Finally, we showcase the utility of ContextCite through three applications: (1) helping verify generated statements (2) improving response quality by pruning the context and (3) detecting poisoning attacks. We provide code for ContextCite at https://github.com/MadryLab/context-cite.

Data Debiasing with Datamodels (D3M): Improving Subgroup Robustness via Data Selection

Machine learning models can fail on subgroups that are underrepresented during training. While techniques such as dataset balancing can improve performance on underperforming groups, they require access to training group annotations and can end up removing large portions of the dataset. In this paper, we introduce Data Debiasing with Datamodels (D3M), a debiasing approach which isolates and removes specific training examples that drive the model's failures on minority groups. Our approach enables us to efficiently train debiased classifiers while removing only a small number of examples, and does not require training group annotations or additional hyperparameter tuning.

The Journey, Not the Destination: How Data Guides Diffusion Models

Diffusion models trained on large datasets can synthesize photo-realistic images of remarkable quality and diversity. However, attributing these images back to the training data-that is, identifying specific training examples which caused an image to be generated-remains a challenge. In this paper, we propose a framework that: (i) provides a formal notion of data attribution in the context of diffusion models, and (ii) allows us to counterfactually validate such attributions. Then, we provide a method for computing these attributions efficiently. Finally, we apply our method to find (and evaluate) such attributions for denoising diffusion probabilistic models trained on CIFAR-10 and latent diffusion models trained on MS COCO. We provide code at https://github.com/MadryLab/journey-TRAK .

Rethinking Backdoor Attacks

In a backdoor attack, an adversary inserts maliciously constructed backdoor examples into a training set to make the resulting model vulnerable to manipulation. Defending against such attacks typically involves viewing these inserted examples as outliers in the training set and using techniques from robust statistics to detect and remove them. In this work, we present a different approach to the backdoor attack problem. Specifically, we show that without structural information about the training data distribution, backdoor attacks are indistinguishable from naturally-occurring features in the data--and thus impossible to "detect" in a general sense. Then, guided by this observation, we revisit existing defenses against backdoor attacks and characterize the (often latent) assumptions they make and on which they depend. Finally, we explore an alternative perspective on backdoor attacks: one that assumes these attacks correspond to the strongest feature in the training data. Under this assumption (which we make formal) we develop a new primitive for detecting backdoor attacks. Our primitive naturally gives rise to a detection algorithm that comes with theoretical guarantees and is effective in practice.

TRAK: Attributing Model Behavior at Scale

The goal of data attribution is to trace model predictions back to training data. Despite a long line of work towards this goal, existing approaches to data attribution tend to force users to choose between computational tractability and efficacy. That is, computationally tractable methods can struggle with accurately attributing model predictions in non-convex settings (e.g., in the context of deep neural networks), while methods that are effective in such regimes require training thousands of models, which makes them impractical for large models or datasets. In this work, we introduce TRAK (Tracing with the Randomly-projected After Kernel), a data attribution method that is both effective and computationally tractable for large-scale, differentiable models. In particular, by leveraging only a handful of trained models, TRAK can match the performance of attribution methods that require training thousands of models. We demonstrate the utility of TRAK across various modalities and scales: image classifiers trained on ImageNet, vision-language models (CLIP), and language models (BERT and mT5). We provide code for using TRAK (and reproducing our work) at https://github.com/MadryLab/trak .

Privacy Induces Robustness: Information-Computation Gaps and Sparse Mean Estimation

We establish a simple connection between robust and differentially-private algorithms: private mechanisms which perform well with very high probability are automatically robust in the sense that they retain accuracy even if a constant fraction of the samples they receive are adversarially corrupted. Since optimal mechanisms typically achieve these high success probabilities, our results imply that optimal private mechanisms for many basic statistics problems are robust. We investigate the consequences of this observation for both algorithms and computational complexity across different statistical problems. Assuming the Brennan-Bresler secret-leakage planted clique conjecture, we demonstrate a fundamental tradeoff between computational efficiency, privacy leakage, and success probability for sparse mean estimation. Private algorithms which match this tradeoff are not yet known -- we achieve that (up to polylogarithmic factors) in a polynomially-large range of parameters via the Sum-of-Squares method. To establish an information-computation gap for private sparse mean estimation, we also design new (exponential-time) mechanisms using fewer samples than efficient algorithms must use. Finally, we give evidence for privacy-induced information-computation gaps for several other statistics and learning problems, including PAC learning parity functions and estimation of the mean of a multivariate Gaussian.

Implicit Bias of Linear Equivariant Networks

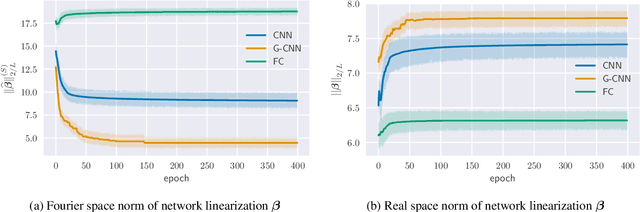
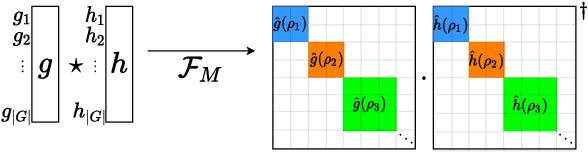
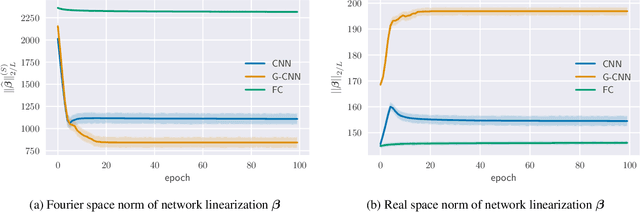
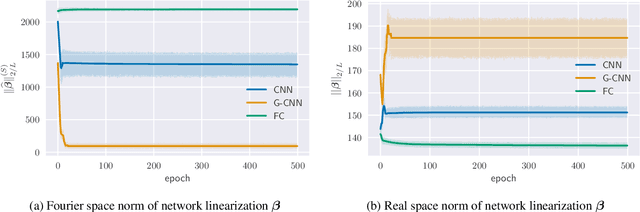
Group equivariant convolutional neural networks (G-CNNs) are generalizations of convolutional neural networks (CNNs) which excel in a wide range of scientific and technical applications by explicitly encoding group symmetries, such as rotations and permutations, in their architectures. Although the success of G-CNNs is driven by the explicit symmetry bias of their convolutional architecture, a recent line of work has proposed that the implicit bias of training algorithms on a particular parameterization (or architecture) is key to understanding generalization for overparameterized neural nets. In this context, we show that $L$-layer full-width linear G-CNNs trained via gradient descent in a binary classification task converge to solutions with low-rank Fourier matrix coefficients, regularized by the $2/L$-Schatten matrix norm. Our work strictly generalizes previous analysis on the implicit bias of linear CNNs to linear G-CNNs over all finite groups, including the challenging setting of non-commutative symmetry groups (such as permutations). We validate our theorems via experiments on a variety of groups and empirically explore more realistic nonlinear networks, which locally capture similar regularization patterns. Finally, we provide intuitive interpretations of our Fourier space implicit regularization results in real space via uncertainty principles.