Deep Policy Gradient Methods Without Batch Updates, Target Networks, or Replay Buffers

Modern deep policy gradient methods achieve effective performance on simulated robotic tasks, but they all require large replay buffers or expensive batch updates, or both, making them incompatible for real systems with resource-limited computers. We show that these methods fail catastrophically when limited to small replay buffers or during incremental learning, where updates only use the most recent sample without batch updates or a replay buffer. We propose a novel incremental deep policy gradient method -- Action Value Gradient (AVG) and a set of normalization and scaling techniques to address the challenges of instability in incremental learning. On robotic simulation benchmarks, we show that AVG is the only incremental method that learns effectively, often achieving final performance comparable to batch policy gradient methods. This advancement enabled us to show for the first time effective deep reinforcement learning with real robots using only incremental updates, employing a robotic manipulator and a mobile robot.

Real-Time Recurrent Learning using Trace Units in Reinforcement Learning

Recurrent Neural Networks (RNNs) are used to learn representations in partially observable environments. For agents that learn online and continually interact with the environment, it is desirable to train RNNs with real-time recurrent learning (RTRL); unfortunately, RTRL is prohibitively expensive for standard RNNs. A promising direction is to use linear recurrent architectures (LRUs), where dense recurrent weights are replaced with a complex-valued diagonal, making RTRL efficient. In this work, we build on these insights to provide a lightweight but effective approach for training RNNs in online RL. We introduce Recurrent Trace Units (RTUs), a small modification on LRUs that we nonetheless find to have significant performance benefits over LRUs when trained with RTRL. We find RTUs significantly outperform other recurrent architectures across several partially observable environments while using significantly less computation.

q-exponential family for policy optimization

Policy optimization methods benefit from a simple and tractable policy functional, usually the Gaussian for continuous action spaces. In this paper, we consider a broader policy family that remains tractable: the $q$-exponential family. This family of policies is flexible, allowing the specification of both heavy-tailed policies ($q>1$) and light-tailed policies ($q<1$). This paper examines the interplay between $q$-exponential policies for several actor-critic algorithms conducted on both online and offline problems. We find that heavy-tailed policies are more effective in general and can consistently improve on Gaussian. In particular, we find the Student's t-distribution to be more stable than the Gaussian across settings and that a heavy-tailed $q$-Gaussian for Tsallis Advantage Weighted Actor-Critic consistently performs well in offline benchmark problems. Our code is available at \url{https://github.com/lingweizhu/qexp}.

The Cross-environment Hyperparameter Setting Benchmark for Reinforcement Learning

This paper introduces a new empirical methodology, the Cross-environment Hyperparameter Setting Benchmark, that compares RL algorithms across environments using a single hyperparameter setting, encouraging algorithmic development which is insensitive to hyperparameters. We demonstrate that this benchmark is robust to statistical noise and obtains qualitatively similar results across repeated applications, even when using few samples. This robustness makes the benchmark computationally cheap to apply, allowing statistically sound insights at low cost. We demonstrate two example instantiations of the CHS, on a set of six small control environments (SC-CHS) and on the entire DM Control suite of 28 environments (DMC-CHS). Finally, to illustrate the applicability of the CHS to modern RL algorithms on challenging environments, we conduct a novel empirical study of an open question in the continuous control literature. We show, with high confidence, that there is no meaningful difference in performance between Ornstein-Uhlenbeck noise and uncorrelated Gaussian noise for exploration with the DDPG algorithm on the DMC-CHS.

Investigating the Interplay of Prioritized Replay and Generalization

Experience replay is ubiquitous in reinforcement learning, to reuse past data and improve sample efficiency. Though a variety of smart sampling schemes have been introduced to improve performance, uniform sampling by far remains the most common approach. One exception is Prioritized Experience Replay (PER), where sampling is done proportionally to TD errors, inspired by the success of prioritized sweeping in dynamic programming. The original work on PER showed improvements in Atari, but follow-up results are mixed. In this paper, we investigate several variations on PER, to attempt to understand where and when PER may be useful. Our findings in prediction tasks reveal that while PER can improve value propagation in tabular settings, behavior is significantly different when combined with neural networks. Certain mitigations -- like delaying target network updates to control generalization and using estimates of expected TD errors in PER to avoid chasing stochasticity -- can avoid large spikes in error with PER and neural networks, but nonetheless generally do not outperform uniform replay. In control tasks, none of the prioritized variants consistently outperform uniform replay.

Position: Benchmarking is Limited in Reinforcement Learning Research

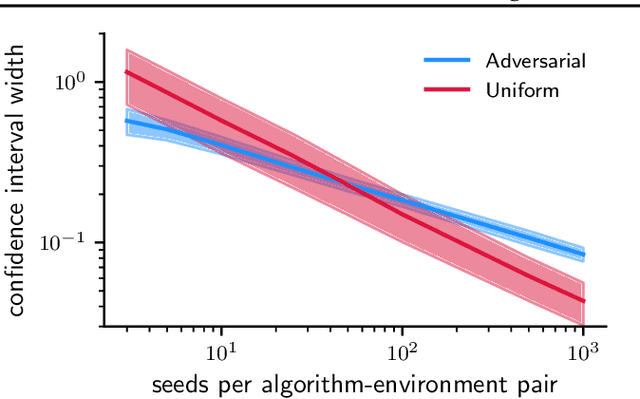
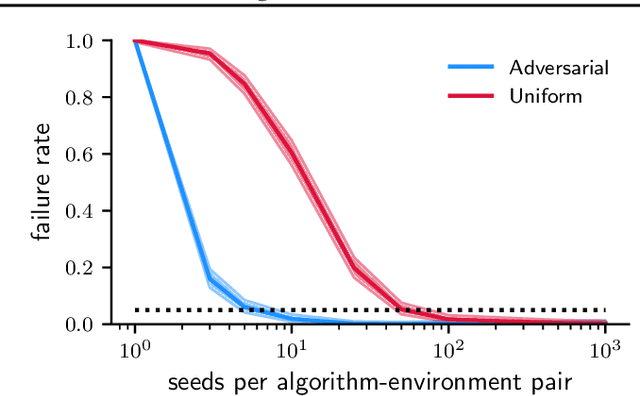
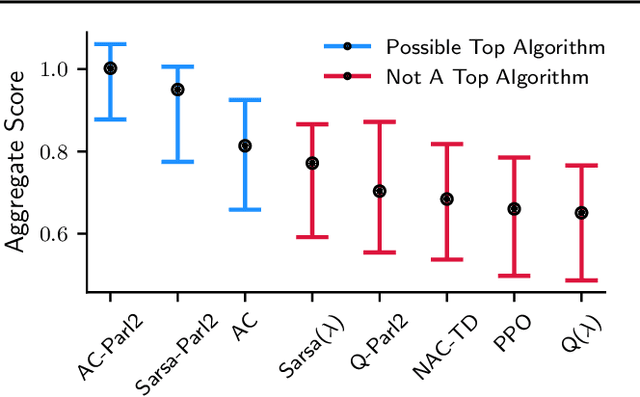
Novel reinforcement learning algorithms, or improvements on existing ones, are commonly justified by evaluating their performance on benchmark environments and are compared to an ever-changing set of standard algorithms. However, despite numerous calls for improvements, experimental practices continue to produce misleading or unsupported claims. One reason for the ongoing substandard practices is that conducting rigorous benchmarking experiments requires substantial computational time. This work investigates the sources of increased computation costs in rigorous experiment designs. We show that conducting rigorous performance benchmarks will likely have computational costs that are often prohibitive. As a result, we argue for using an additional experimentation paradigm to overcome the limitations of benchmarking.

Demystifying the Recency Heuristic in Temporal-Difference Learning

The recency heuristic in reinforcement learning is the assumption that stimuli that occurred closer in time to an acquired reward should be more heavily reinforced. The recency heuristic is one of the key assumptions made by TD($\lambda$), which reinforces recent experiences according to an exponentially decaying weighting. In fact, all other widely used return estimators for TD learning, such as $n$-step returns, satisfy a weaker (i.e., non-monotonic) recency heuristic. Why is the recency heuristic effective for temporal credit assignment? What happens when credit is assigned in a way that violates this heuristic? In this paper, we analyze the specific mathematical implications of adopting the recency heuristic in TD learning. We prove that any return estimator satisfying this heuristic: 1) is guaranteed to converge to the correct value function, 2) has a relatively fast contraction rate, and 3) has a long window of effective credit assignment, yet bounded worst-case variance. We also give a counterexample where on-policy, tabular TD methods violating the recency heuristic diverge. Our results offer some of the first theoretical evidence that credit assignment based on the recency heuristic facilitates learning.

A New View on Planning in Online Reinforcement Learning

This paper investigates a new approach to model-based reinforcement learning using background planning: mixing (approximate) dynamic programming updates and model-free updates, similar to the Dyna architecture. Background planning with learned models is often worse than model-free alternatives, such as Double DQN, even though the former uses significantly more memory and computation. The fundamental problem is that learned models can be inaccurate and often generate invalid states, especially when iterated many steps. In this paper, we avoid this limitation by constraining background planning to a set of (abstract) subgoals and learning only local, subgoal-conditioned models. This goal-space planning (GSP) approach is more computationally efficient, naturally incorporates temporal abstraction for faster long-horizon planning and avoids learning the transition dynamics entirely. We show that our GSP algorithm can propagate value from an abstract space in a manner that helps a variety of base learners learn significantly faster in different domains.

Tuning for the Unknown: Revisiting Evaluation Strategies for Lifelong RL

In continual or lifelong reinforcement learning access to the environment should be limited. If we aspire to design algorithms that can run for long-periods of time, continually adapting to new, unexpected situations then we must be willing to deploy our agents without tuning their hyperparameters over the agent's entire lifetime. The standard practice in deep RL -- and even continual RL -- is to assume unfettered access to deployment environment for the full lifetime of the agent. This paper explores the notion that progress in lifelong RL research has been held back by inappropriate empirical methodologies. In this paper we propose a new approach for tuning and evaluating lifelong RL agents where only one percent of the experiment data can be used for hyperparameter tuning. We then conduct an empirical study of DQN and Soft Actor Critic across a variety of continuing and non-stationary domains. We find both methods generally perform poorly when restricted to one-percent tuning, whereas several algorithmic mitigations designed to maintain network plasticity perform surprising well. In addition, we find that properties designed to measure the network's ability to learn continually indeed correlate with performance under one-percent tuning.

Investigating the Histogram Loss in Regression

It is becoming increasingly common in regression to train neural networks that model the entire distribution even if only the mean is required for prediction. This additional modeling often comes with performance gain and the reasons behind the improvement are not fully known. This paper investigates a recent approach to regression, the Histogram Loss, which involves learning the conditional distribution of the target variable by minimizing the cross-entropy between a target distribution and a flexible histogram prediction. We design theoretical and empirical analyses to determine why and when this performance gain appears, and how different components of the loss contribute to it. Our results suggest that the benefits of learning distributions in this setup come from improvements in optimization rather than learning a better representation. We then demonstrate the viability of the Histogram Loss in common deep learning applications without a need for costly hyperparameter tuning.