Unsupervised Learning of 3D Structure from Images

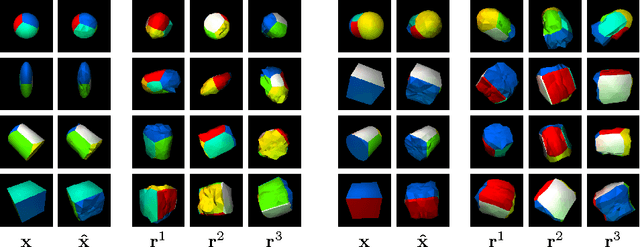
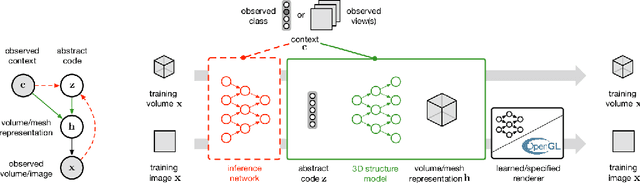
A key goal of computer vision is to recover the underlying 3D structure from 2D observations of the world. In this paper we learn strong deep generative models of 3D structures, and recover these structures from 3D and 2D images via probabilistic inference. We demonstrate high-quality samples and report log-likelihoods on several datasets, including ShapeNet [2], and establish the first benchmarks in the literature. We also show how these models and their inference networks can be trained end-to-end from 2D images. This demonstrates for the first time the feasibility of learning to infer 3D representations of the world in a purely unsupervised manner.

Distribution Matching in Variational Inference

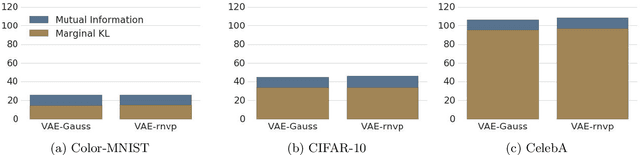
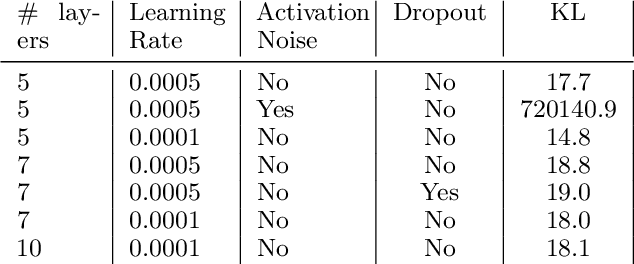
We show that Variational Autoencoders consistently fail to learn marginal distributions in latent and visible space. We ask whether this is a consequence of matching conditional distributions, or a limitation of explicit model and posterior distributions. We explore alternatives provided by marginal distribution matching and implicit distributions through the use of Generative Adversarial Networks in variational inference. We perform a large-scale evaluation of several VAE-GAN hybrids and explore the implications of class probability estimation for learning distributions. We conclude that at present VAE-GAN hybrids have limited applicability: they are harder to scale, evaluate, and use for inference compared to VAEs; and they do not improve over the generation quality of GANs.

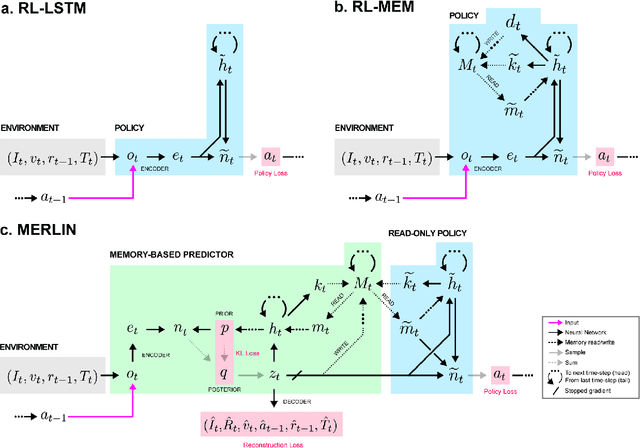
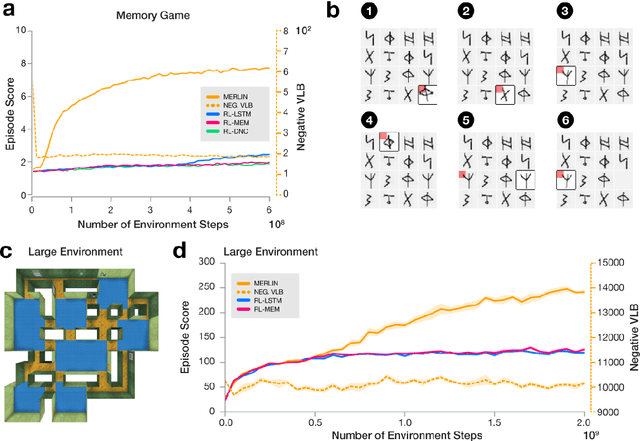
Unsupervised Predictive Memory in a Goal-Directed Agent

Animals execute goal-directed behaviours despite the limited range and scope of their sensors. To cope, they explore environments and store memories maintaining estimates of important information that is not presently available. Recently, progress has been made with artificial intelligence (AI) agents that learn to perform tasks from sensory input, even at a human level, by merging reinforcement learning (RL) algorithms with deep neural networks, and the excitement surrounding these results has led to the pursuit of related ideas as explanations of non-human animal learning. However, we demonstrate that contemporary RL algorithms struggle to solve simple tasks when enough information is concealed from the sensors of the agent, a property called "partial observability". An obvious requirement for handling partially observed tasks is access to extensive memory, but we show memory is not enough; it is critical that the right information be stored in the right format. We develop a model, the Memory, RL, and Inference Network (MERLIN), in which memory formation is guided by a process of predictive modeling. MERLIN facilitates the solution of tasks in 3D virtual reality environments for which partial observability is severe and memories must be maintained over long durations. Our model demonstrates a single learning agent architecture that can solve canonical behavioural tasks in psychology and neurobiology without strong simplifying assumptions about the dimensionality of sensory input or the duration of experiences.

Many Paths to Equilibrium: GANs Do Not Need to Decrease a Divergence At Every Step

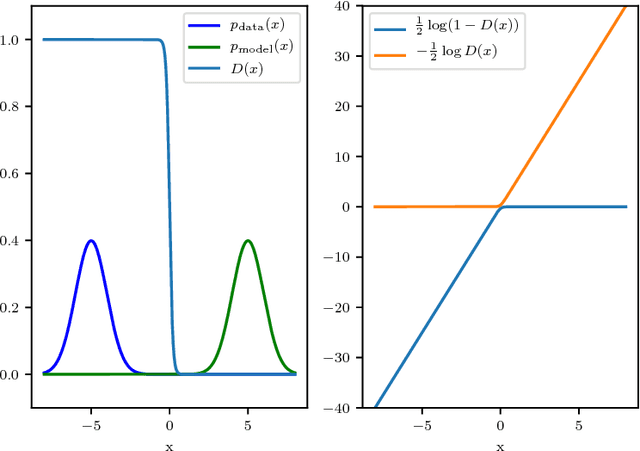
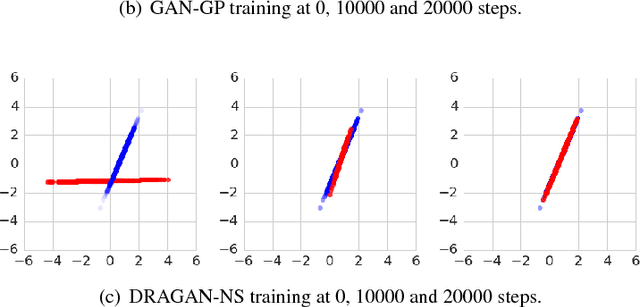
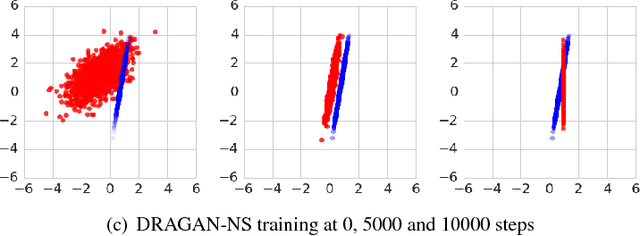
Generative adversarial networks (GANs) are a family of generative models that do not minimize a single training criterion. Unlike other generative models, the data distribution is learned via a game between a generator (the generative model) and a discriminator (a teacher providing training signal) that each minimize their own cost. GANs are designed to reach a Nash equilibrium at which each player cannot reduce their cost without changing the other players' parameters. One useful approach for the theory of GANs is to show that a divergence between the training distribution and the model distribution obtains its minimum value at equilibrium. Several recent research directions have been motivated by the idea that this divergence is the primary guide for the learning process and that every step of learning should decrease the divergence. We show that this view is overly restrictive. During GAN training, the discriminator provides learning signal in situations where the gradients of the divergences between distributions would not be useful. We provide empirical counterexamples to the view of GAN training as divergence minimization. Specifically, we demonstrate that GANs are able to learn distributions in situations where the divergence minimization point of view predicts they would fail. We also show that gradient penalties motivated from the divergence minimization perspective are equally helpful when applied in other contexts in which the divergence minimization perspective does not predict they would be helpful. This contributes to a growing body of evidence that GAN training may be more usefully viewed as approaching Nash equilibria via trajectories that do not necessarily minimize a specific divergence at each step.

Variational Approaches for Auto-Encoding Generative Adversarial Networks

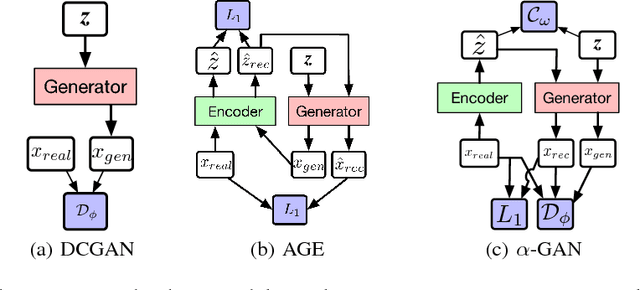
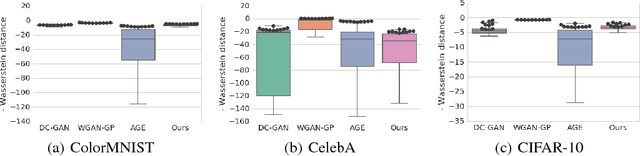
Auto-encoding generative adversarial networks (GANs) combine the standard GAN algorithm, which discriminates between real and model-generated data, with a reconstruction loss given by an auto-encoder. Such models aim to prevent mode collapse in the learned generative model by ensuring that it is grounded in all the available training data. In this paper, we develop a principle upon which auto-encoders can be combined with generative adversarial networks by exploiting the hierarchical structure of the generative model. The underlying principle shows that variational inference can be used a basic tool for learning, but with the in- tractable likelihood replaced by a synthetic likelihood, and the unknown posterior distribution replaced by an implicit distribution; both synthetic likelihoods and implicit posterior distributions can be learned using discriminators. This allows us to develop a natural fusion of variational auto-encoders and generative adversarial networks, combining the best of both these methods. We describe a unified objective for optimization, discuss the constraints needed to guide learning, connect to the wide range of existing work, and use a battery of tests to systematically and quantitatively assess the performance of our method.

The Cramer Distance as a Solution to Biased Wasserstein Gradients

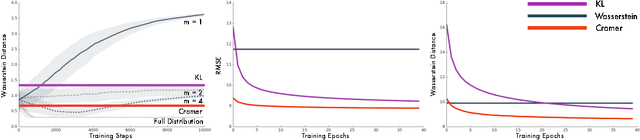
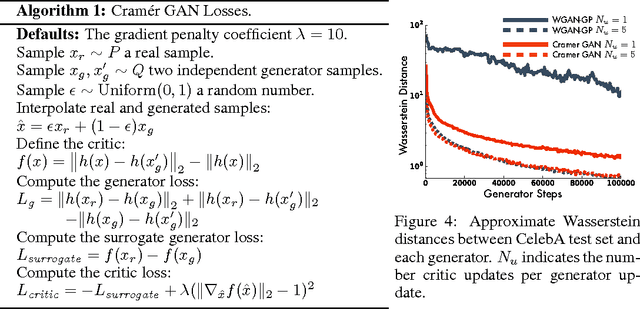
The Wasserstein probability metric has received much attention from the machine learning community. Unlike the Kullback-Leibler divergence, which strictly measures change in probability, the Wasserstein metric reflects the underlying geometry between outcomes. The value of being sensitive to this geometry has been demonstrated, among others, in ordinal regression and generative modelling. In this paper we describe three natural properties of probability divergences that reflect requirements from machine learning: sum invariance, scale sensitivity, and unbiased sample gradients. The Wasserstein metric possesses the first two properties but, unlike the Kullback-Leibler divergence, does not possess the third. We provide empirical evidence suggesting that this is a serious issue in practice. Leveraging insights from probabilistic forecasting we propose an alternative to the Wasserstein metric, the Cram\'er distance. We show that the Cram\'er distance possesses all three desired properties, combining the best of the Wasserstein and Kullback-Leibler divergences. To illustrate the relevance of the Cram\'er distance in practice we design a new algorithm, the Cram\'er Generative Adversarial Network (GAN), and show that it performs significantly better than the related Wasserstein GAN.

Recurrent Environment Simulators

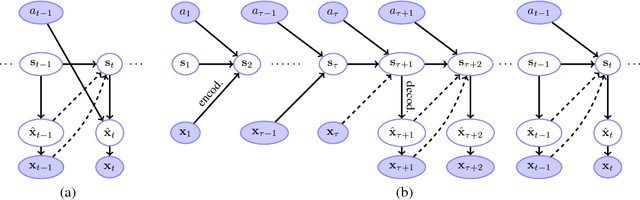
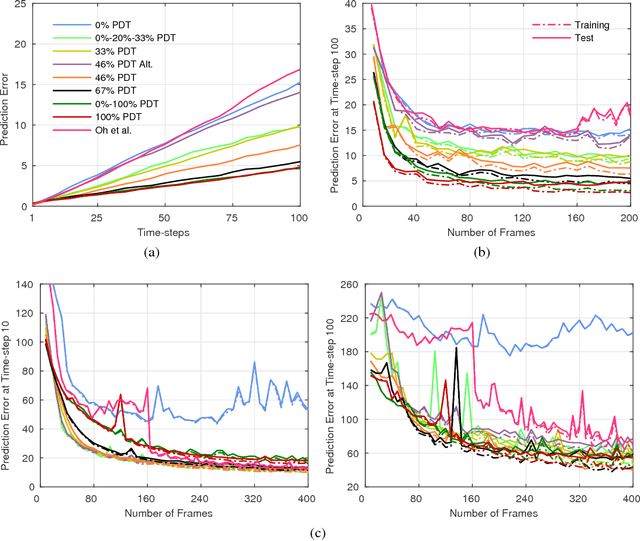
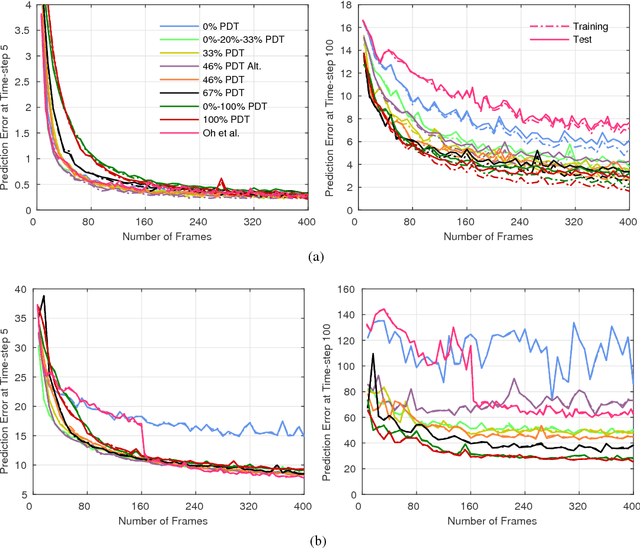
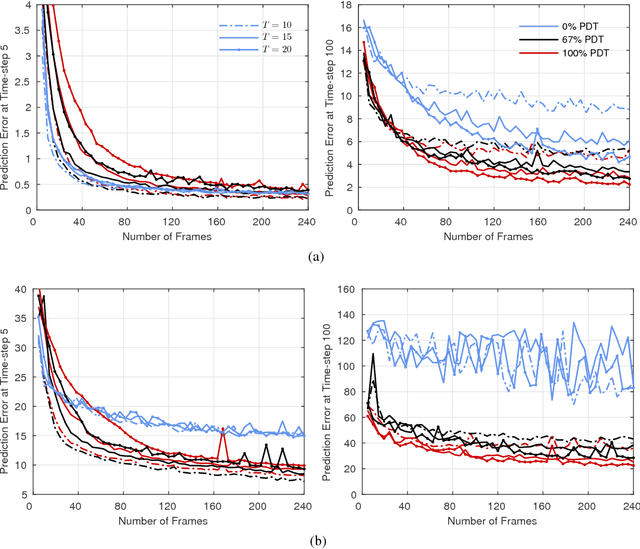
Models that can simulate how environments change in response to actions can be used by agents to plan and act efficiently. We improve on previous environment simulators from high-dimensional pixel observations by introducing recurrent neural networks that are able to make temporally and spatially coherent predictions for hundreds of time-steps into the future. We present an in-depth analysis of the factors affecting performance, providing the most extensive attempt to advance the understanding of the properties of these models. We address the issue of computationally inefficiency with a model that does not need to generate a high-dimensional image at each time-step. We show that our approach can be used to improve exploration and is adaptable to many diverse environments, namely 10 Atari games, a 3D car racing environment, and complex 3D mazes.

Learning in Implicit Generative Models

Generative adversarial networks (GANs) provide an algorithmic framework for constructing generative models with several appealing properties: they do not require a likelihood function to be specified, only a generating procedure; they provide samples that are sharp and compelling; and they allow us to harness our knowledge of building highly accurate neural network classifiers. Here, we develop our understanding of GANs with the aim of forming a rich view of this growing area of machine learning---to build connections to the diverse set of statistical thinking on this topic, of which much can be gained by a mutual exchange of ideas. We frame GANs within the wider landscape of algorithms for learning in implicit generative models--models that only specify a stochastic procedure with which to generate data--and relate these ideas to modelling problems in related fields, such as econometrics and approximate Bayesian computation. We develop likelihood-free inference methods and highlight hypothesis testing as a principle for learning in implicit generative models, using which we are able to derive the objective function used by GANs, and many other related objectives. The testing viewpoint directs our focus to the general problem of density ratio estimation. There are four approaches for density ratio estimation, one of which is a solution using classifiers to distinguish real from generated data. Other approaches such as divergence minimisation and moment matching have also been explored in the GAN literature, and we synthesise these views to form an understanding in terms of the relationships between them and the wider literature, highlighting avenues for future exploration and cross-pollination.

Generative Temporal Models with Memory

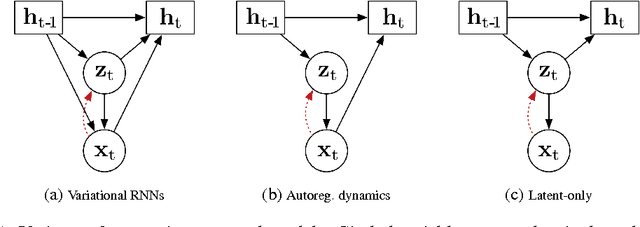
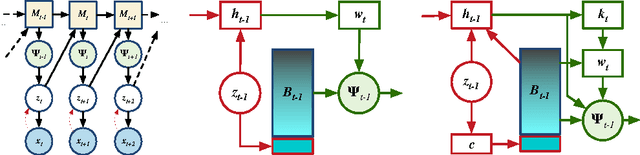
We consider the general problem of modeling temporal data with long-range dependencies, wherein new observations are fully or partially predictable based on temporally-distant, past observations. A sufficiently powerful temporal model should separate predictable elements of the sequence from unpredictable elements, express uncertainty about those unpredictable elements, and rapidly identify novel elements that may help to predict the future. To create such models, we introduce Generative Temporal Models augmented with external memory systems. They are developed within the variational inference framework, which provides both a practical training methodology and methods to gain insight into the models' operation. We show, on a range of problems with sparse, long-term temporal dependencies, that these models store information from early in a sequence, and reuse this stored information efficiently. This allows them to perform substantially better than existing models based on well-known recurrent neural networks, like LSTMs.

Normalizing Flows on Riemannian Manifolds

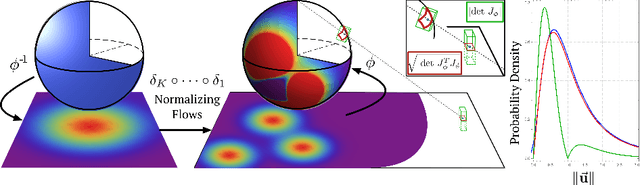
We consider the problem of density estimation on Riemannian manifolds. Density estimation on manifolds has many applications in fluid-mechanics, optics and plasma physics and it appears often when dealing with angular variables (such as used in protein folding, robot limbs, gene-expression) and in general directional statistics. In spite of the multitude of algorithms available for density estimation in the Euclidean spaces $\mathbf{R}^n$ that scale to large n (e.g. normalizing flows, kernel methods and variational approximations), most of these methods are not immediately suitable for density estimation in more general Riemannian manifolds. We revisit techniques related to homeomorphisms from differential geometry for projecting densities to sub-manifolds and use it to generalize the idea of normalizing flows to more general Riemannian manifolds. The resulting algorithm is scalable, simple to implement and suitable for use with automatic differentiation. We demonstrate concrete examples of this method on the n-sphere $\mathbf{S}^n$.