Neural Compression of Atmospheric States

Atmospheric states derived from reanalysis comprise a substantial portion of weather and climate simulation outputs. Many stakeholders -- such as researchers, policy makers, and insurers -- use this data to better understand the earth system and guide policy decisions. Atmospheric states have also received increased interest as machine learning approaches to weather prediction have shown promising results. A key issue for all audiences is that dense time series of these high-dimensional states comprise an enormous amount of data, precluding all but the most well resourced groups from accessing and using historical data and future projections. To address this problem, we propose a method for compressing atmospheric states using methods from the neural network literature, adapting spherical data to processing by conventional neural architectures through the use of the area-preserving HEALPix projection. We investigate two model classes for building neural compressors: the hyperprior model from the neural image compression literature and recent vector-quantised models. We show that both families of models satisfy the desiderata of small average error, a small number of high-error reconstructed pixels, faithful reproduction of extreme events such as hurricanes and heatwaves, preservation of the spectral power distribution across spatial scales. We demonstrate compression ratios in excess of 1000x, with compression and decompression at a rate of approximately one second per global atmospheric state.

Evaluating Model Bias Requires Characterizing its Mistakes

The ability to properly benchmark model performance in the face of spurious correlations is important to both build better predictors and increase confidence that models are operating as intended. We demonstrate that characterizing (as opposed to simply quantifying) model mistakes across subgroups is pivotal to properly reflect model biases, which are ignored by standard metrics such as worst-group accuracy or accuracy gap. Inspired by the hypothesis testing framework, we introduce SkewSize, a principled and flexible metric that captures bias from mistakes in a model's predictions. It can be used in multi-class settings or generalised to the open vocabulary setting of generative models. SkewSize is an aggregation of the effect size of the interaction between two categorical variables: the spurious variable representing the bias attribute and the model's prediction. We demonstrate the utility of SkewSize in multiple settings including: standard vision models trained on synthetic data, vision models trained on ImageNet, and large scale vision-and-language models from the BLIP-2 family. In each case, the proposed SkewSize is able to highlight biases not captured by other metrics, while also providing insights on the impact of recently proposed techniques, such as instruction tuning.

Solving MaxSAT with Matrix Multiplication

We propose an incomplete algorithm for Maximum Satisfiability (MaxSAT) specifically designed to run on neural network accelerators such as GPUs and TPUs. Given a MaxSAT problem instance in conjunctive normal form, our procedure constructs a Restricted Boltzmann Machine (RBM) with an equilibrium distribution wherein the probability of a Boolean assignment is exponential in the number of clauses it satisfies. Block Gibbs sampling is used to stochastically search the space of assignments with parallel Markov chains. Since matrix multiplication is the main computational primitive for block Gibbs sampling in an RBM, our approach leads to an elegantly simple algorithm (40 lines of JAX) well-suited for neural network accelerators. Theoretical results about RBMs guarantee that the required number of visible and hidden units of the RBM scale only linearly with the number of variables and constant-sized clauses in the MaxSAT instance, ensuring that the computational cost of a Gibbs step scales reasonably with the instance size. Search throughput can be increased by batching parallel chains within a single accelerator as well as by distributing them across multiple accelerators. As a further enhancement, a heuristic based on unit propagation running on CPU is periodically applied to the sampled assignments. Our approach, which we term RbmSAT, is a new design point in the algorithm-hardware co-design space for MaxSAT. We present timed results on a subset of problem instances from the annual MaxSAT Evaluation's Incomplete Unweighted Track for the years 2018 to 2021. When allotted the same running time and CPU compute budget (but no TPUs), RbmSAT outperforms other participating solvers on problems drawn from three out of the four years' competitions. Given the same running time on a TPU cluster for which RbmSAT is uniquely designed, it outperforms all solvers on problems drawn from all four years.

Learning more skills through optimistic exploration

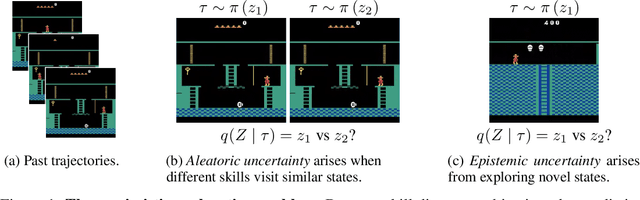
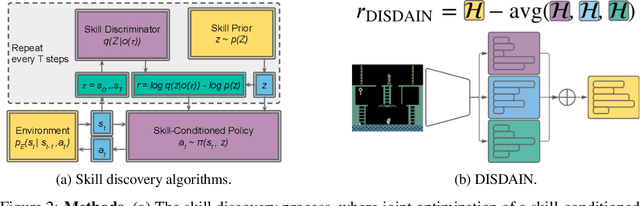
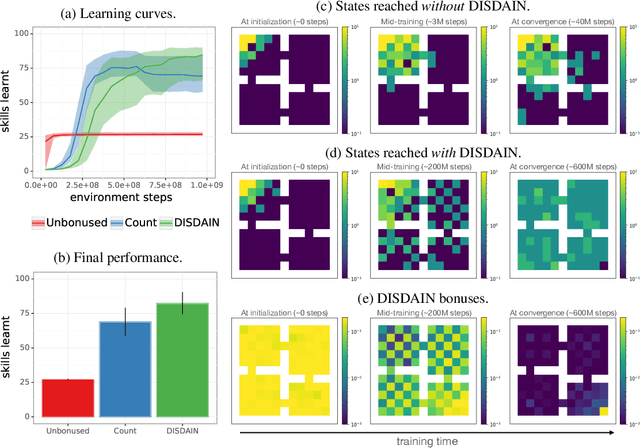
Unsupervised skill learning objectives (Gregor et al., 2016, Eysenbach et al., 2018) allow agents to learn rich repertoires of behavior in the absence of extrinsic rewards. They work by simultaneously training a policy to produce distinguishable latent-conditioned trajectories, and a discriminator to evaluate distinguishability by trying to infer latents from trajectories. The hope is for the agent to explore and master the environment by encouraging each skill (latent) to reliably reach different states. However, an inherent exploration problem lingers: when a novel state is actually encountered, the discriminator will necessarily not have seen enough training data to produce accurate and confident skill classifications, leading to low intrinsic reward for the agent and effective penalization of the sort of exploration needed to actually maximize the objective. To combat this inherent pessimism towards exploration, we derive an information gain auxiliary objective that involves training an ensemble of discriminators and rewarding the policy for their disagreement. Our objective directly estimates the epistemic uncertainty that comes from the discriminator not having seen enough training examples, thus providing an intrinsic reward more tailored to the true objective compared to pseudocount-based methods (Burda et al., 2019). We call this exploration bonus discriminator disagreement intrinsic reward, or DISDAIN. We demonstrate empirically that DISDAIN improves skill learning both in a tabular grid world (Four Rooms) and the 57 games of the Atari Suite (from pixels). Thus, we encourage researchers to treat pessimism with DISDAIN.

Relative Variational Intrinsic Control

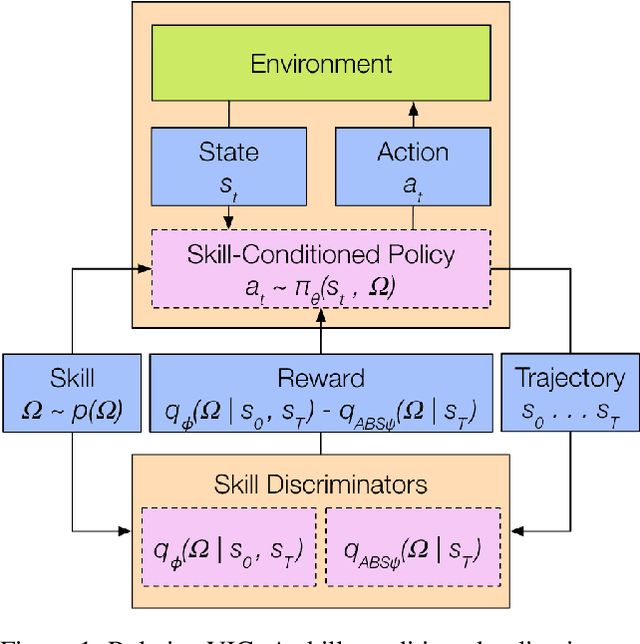
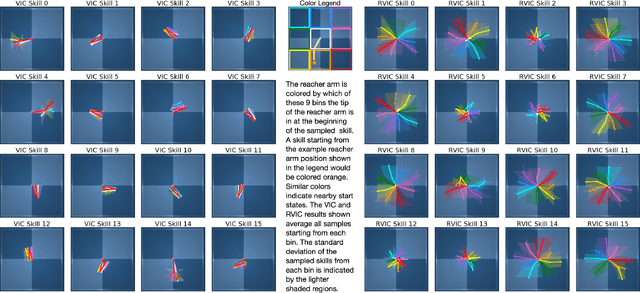
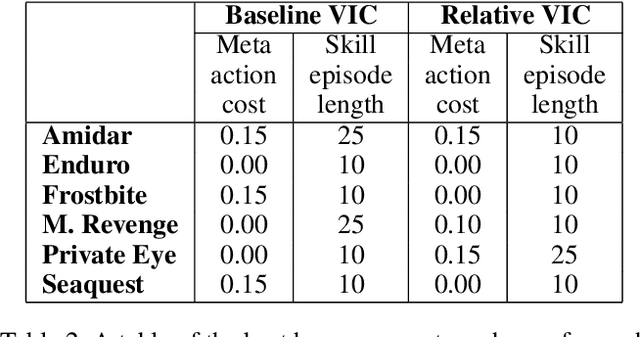
In the absence of external rewards, agents can still learn useful behaviors by identifying and mastering a set of diverse skills within their environment. Existing skill learning methods use mutual information objectives to incentivize each skill to be diverse and distinguishable from the rest. However, if care is not taken to constrain the ways in which the skills are diverse, trivially diverse skill sets can arise. To ensure useful skill diversity, we propose a novel skill learning objective, Relative Variational Intrinsic Control (RVIC), which incentivizes learning skills that are distinguishable in how they change the agent's relationship to its environment. The resulting set of skills tiles the space of affordances available to the agent. We qualitatively analyze skill behaviors on multiple environments and show how RVIC skills are more useful than skills discovered by existing methods when used in hierarchical reinforcement learning.

Q-Learning in enormous action spaces via amortized approximate maximization

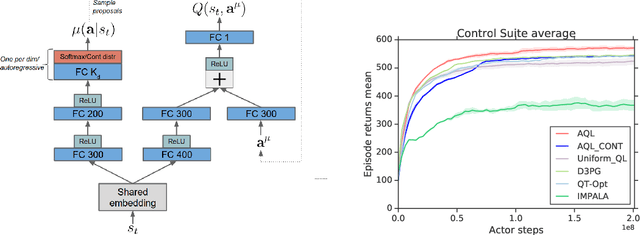
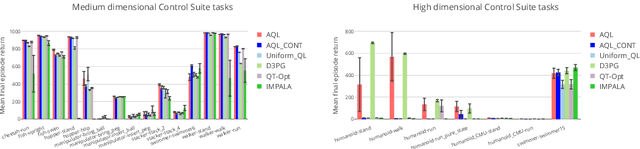
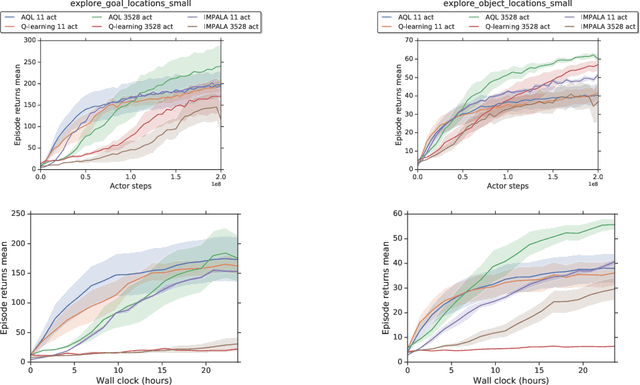
Applying Q-learning to high-dimensional or continuous action spaces can be difficult due to the required maximization over the set of possible actions. Motivated by techniques from amortized inference, we replace the expensive maximization over all actions with a maximization over a small subset of possible actions sampled from a learned proposal distribution. The resulting approach, which we dub Amortized Q-learning (AQL), is able to handle discrete, continuous, or hybrid action spaces while maintaining the benefits of Q-learning. Our experiments on continuous control tasks with up to 21 dimensional actions show that AQL outperforms D3PG (Barth-Maron et al, 2018) and QT-Opt (Kalashnikov et al, 2018). Experiments on structured discrete action spaces demonstrate that AQL can efficiently learn good policies in spaces with thousands of discrete actions.

Fast Task Inference with Variational Intrinsic Successor Features

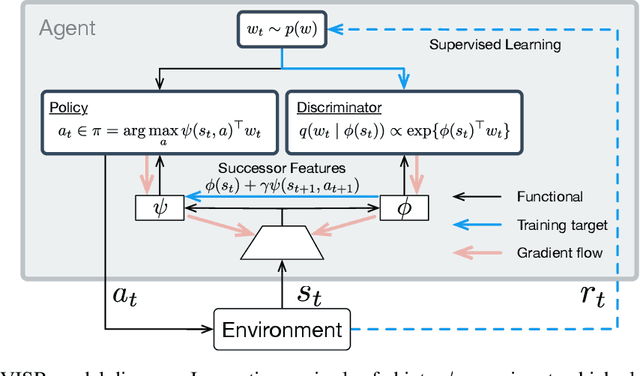
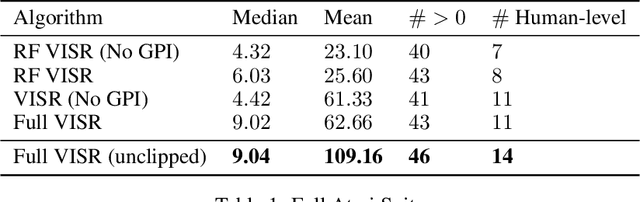
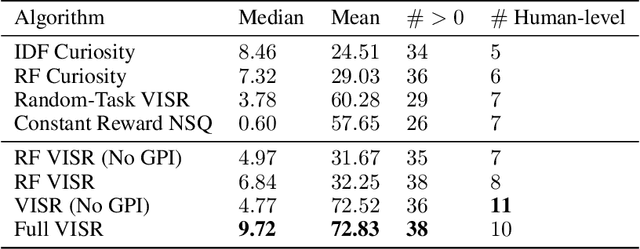
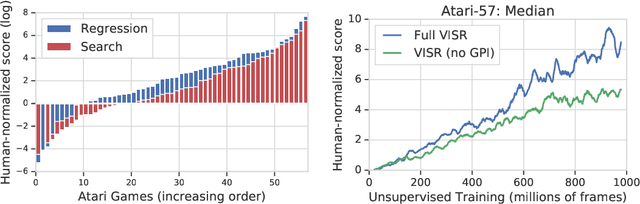
It has been established that diverse behaviors spanning the controllable subspace of an Markov decision process can be trained by rewarding a policy for being distinguishable from other policies \citep{gregor2016variational, eysenbach2018diversity, warde2018unsupervised}. However, one limitation of this formulation is generalizing behaviors beyond the finite set being explicitly learned, as is needed for use on subsequent tasks. Successor features \citep{dayan93improving, barreto2017successor} provide an appealing solution to this generalization problem, but require defining the reward function as linear in some grounded feature space. In this paper, we show that these two techniques can be combined, and that each method solves the other's primary limitation. To do so we introduce Variational Intrinsic Successor FeatuRes (VISR), a novel algorithm which learns controllable features that can be leveraged to provide enhanced generalization and fast task inference through the successor feature framework. We empirically validate VISR on the full Atari suite, in a novel setup wherein the rewards are only exposed briefly after a long unsupervised phase. Achieving human-level performance on 14 games and beating all baselines, we believe VISR represents a step towards agents that rapidly learn from limited feedback.

Unsupervised Control Through Non-Parametric Discriminative Rewards

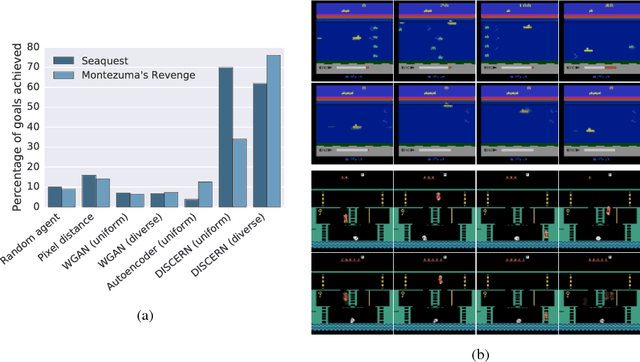
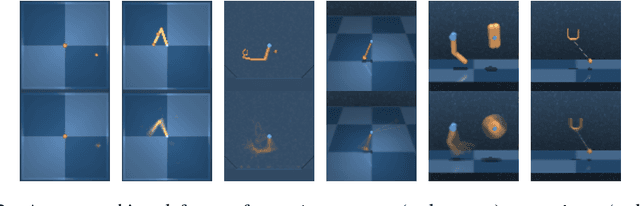
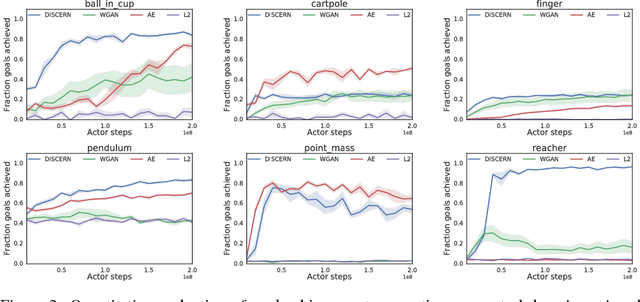
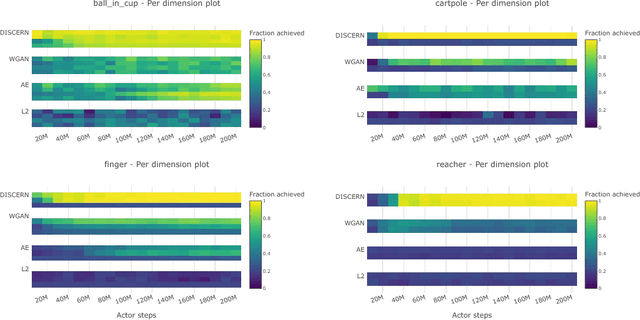
Learning to control an environment without hand-crafted rewards or expert data remains challenging and is at the frontier of reinforcement learning research. We present an unsupervised learning algorithm to train agents to achieve perceptually-specified goals using only a stream of observations and actions. Our agent simultaneously learns a goal-conditioned policy and a goal achievement reward function that measures how similar a state is to the goal state. This dual optimization leads to a co-operative game, giving rise to a learned reward function that reflects similarity in controllable aspects of the environment instead of distance in the space of observations. We demonstrate the efficacy of our agent to learn, in an unsupervised manner, to reach a diverse set of goals on three domains -- Atari, the DeepMind Control Suite and DeepMind Lab.

Variational Approaches for Auto-Encoding Generative Adversarial Networks

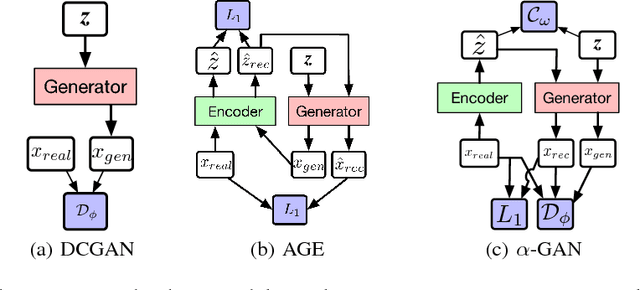
Auto-encoding generative adversarial networks (GANs) combine the standard GAN algorithm, which discriminates between real and model-generated data, with a reconstruction loss given by an auto-encoder. Such models aim to prevent mode collapse in the learned generative model by ensuring that it is grounded in all the available training data. In this paper, we develop a principle upon which auto-encoders can be combined with generative adversarial networks by exploiting the hierarchical structure of the generative model. The underlying principle shows that variational inference can be used a basic tool for learning, but with the in- tractable likelihood replaced by a synthetic likelihood, and the unknown posterior distribution replaced by an implicit distribution; both synthetic likelihoods and implicit posterior distributions can be learned using discriminators. This allows us to develop a natural fusion of variational auto-encoders and generative adversarial networks, combining the best of both these methods. We describe a unified objective for optimization, discuss the constraints needed to guide learning, connect to the wide range of existing work, and use a battery of tests to systematically and quantitatively assess the performance of our method.

Brain Tumor Segmentation with Deep Neural Networks

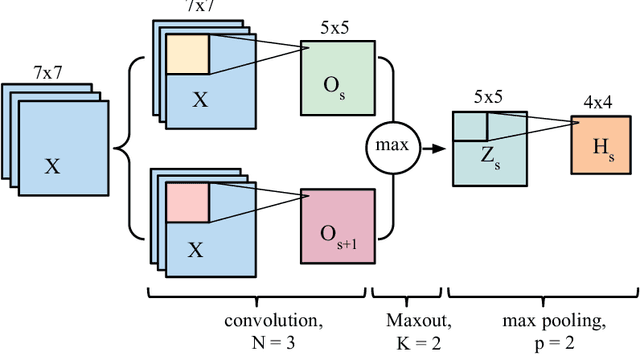
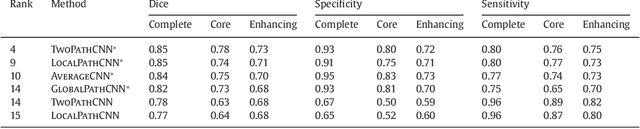
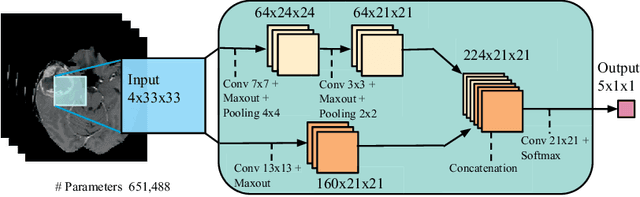
In this paper, we present a fully automatic brain tumor segmentation method based on Deep Neural Networks (DNNs). The proposed networks are tailored to glioblastomas (both low and high grade) pictured in MR images. By their very nature, these tumors can appear anywhere in the brain and have almost any kind of shape, size, and contrast. These reasons motivate our exploration of a machine learning solution that exploits a flexible, high capacity DNN while being extremely efficient. Here, we give a description of different model choices that we've found to be necessary for obtaining competitive performance. We explore in particular different architectures based on Convolutional Neural Networks (CNN), i.e. DNNs specifically adapted to image data. We present a novel CNN architecture which differs from those traditionally used in computer vision. Our CNN exploits both local features as well as more global contextual features simultaneously. Also, different from most traditional uses of CNNs, our networks use a final layer that is a convolutional implementation of a fully connected layer which allows a 40 fold speed up. We also describe a 2-phase training procedure that allows us to tackle difficulties related to the imbalance of tumor labels. Finally, we explore a cascade architecture in which the output of a basic CNN is treated as an additional source of information for a subsequent CNN. Results reported on the 2013 BRATS test dataset reveal that our architecture improves over the currently published state-of-the-art while being over 30 times faster.