MUVERA: Multi-Vector Retrieval via Fixed Dimensional Encodings

Neural embedding models have become a fundamental component of modern information retrieval (IR) pipelines. These models produce a single embedding $x \in \mathbb{R}^d$ per data-point, allowing for fast retrieval via highly optimized maximum inner product search (MIPS) algorithms. Recently, beginning with the landmark ColBERT paper, multi-vector models, which produce a set of embedding per data point, have achieved markedly superior performance for IR tasks. Unfortunately, using these models for IR is computationally expensive due to the increased complexity of multi-vector retrieval and scoring. In this paper, we introduce MUVERA (MUlti-VEctor Retrieval Algorithm), a retrieval mechanism which reduces multi-vector similarity search to single-vector similarity search. This enables the usage of off-the-shelf MIPS solvers for multi-vector retrieval. MUVERA asymmetrically generates Fixed Dimensional Encodings (FDEs) of queries and documents, which are vectors whose inner product approximates multi-vector similarity. We prove that FDEs give high-quality $\epsilon$-approximations, thus providing the first single-vector proxy for multi-vector similarity with theoretical guarantees. Empirically, we find that FDEs achieve the same recall as prior state-of-the-art heuristics while retrieving 2-5$\times$ fewer candidates. Compared to prior state of the art implementations, MUVERA achieves consistently good end-to-end recall and latency across a diverse set of the BEIR retrieval datasets, achieving an average of 10$\%$ improved recall with $90\%$ lower latency.

Unleashing Graph Partitioning for Large-Scale Nearest Neighbor Search

We consider the fundamental problem of decomposing a large-scale approximate nearest neighbor search (ANNS) problem into smaller sub-problems. The goal is to partition the input points into neighborhood-preserving shards, so that the nearest neighbors of any point are contained in only a few shards. When a query arrives, a routing algorithm is used to identify the shards which should be searched for its nearest neighbors. This approach forms the backbone of distributed ANNS, where the dataset is so large that it must be split across multiple machines. In this paper, we design simple and highly efficient routing methods, and prove strong theoretical guarantees on their performance. A crucial characteristic of our routing algorithms is that they are inherently modular, and can be used with any partitioning method. This addresses a key drawback of prior approaches, where the routing algorithms are inextricably linked to their associated partitioning method. In particular, our new routing methods enable the use of balanced graph partitioning, which is a high-quality partitioning method without a naturally associated routing algorithm. Thus, we provide the first methods for routing using balanced graph partitioning that are extremely fast to train, admit low latency, and achieve high recall. We provide a comprehensive evaluation of our full partitioning and routing pipeline on billion-scale datasets, where it outperforms existing scalable partitioning methods by significant margins, achieving up to 2.14x higher QPS at 90% recall$@10$ than the best competitor.

A quasi-polynomial time algorithm for Multi-Dimensional Scaling via LP hierarchies

Multi-dimensional Scaling (MDS) is a family of methods for embedding pair-wise dissimilarities between $n$ objects into low-dimensional space. MDS is widely used as a data visualization tool in the social and biological sciences, statistics, and machine learning. We study the Kamada-Kawai formulation of MDS: given a set of non-negative dissimilarities $\{d_{i,j}\}_{i , j \in [n]}$ over $n$ points, the goal is to find an embedding $\{x_1,\dots,x_n\} \subset \mathbb{R}^k$ that minimizes \[ \text{OPT} = \min_{x} \mathbb{E}_{i,j \in [n]} \left[ \left(1-\frac{\|x_i - x_j\|}{d_{i,j}}\right)^2 \right] \] Despite its popularity, our theoretical understanding of MDS is extremely limited. Recently, Demaine, Hesterberg, Koehler, Lynch, and Urschel (arXiv:2109.11505) gave the first approximation algorithm with provable guarantees for Kamada-Kawai, which achieves an embedding with cost $\text{OPT} +\epsilon$ in $n^2 \cdot 2^{\tilde{\mathcal{O}}(k \Delta^4 / \epsilon^2)}$ time, where $\Delta$ is the aspect ratio of the input dissimilarities. In this work, we give the first approximation algorithm for MDS with quasi-polynomial dependency on $\Delta$: for target dimension $k$, we achieve a solution with cost $\mathcal{O}(\text{OPT}^{ \hspace{0.04in}1/k } \cdot \log(\Delta/\epsilon) )+ \epsilon$ in time $n^{ \mathcal{O}(1)} \cdot 2^{\tilde{\mathcal{O}}( k^2 (\log(\Delta)/\epsilon)^{k/2 + 1} ) }$. Our approach is based on a novel analysis of a conditioning-based rounding scheme for the Sherali-Adams LP Hierarchy. Crucially, our analysis exploits the geometry of low-dimensional Euclidean space, allowing us to avoid an exponential dependence on the aspect ratio $\Delta$. We believe our geometry-aware treatment of the Sherali-Adams Hierarchy is an important step towards developing general-purpose techniques for efficient metric optimization algorithms.

HyperAttention: Long-context Attention in Near-Linear Time

We present an approximate attention mechanism named HyperAttention to address the computational challenges posed by the growing complexity of long contexts used in Large Language Models (LLMs). Recent work suggests that in the worst-case scenario, quadratic time is necessary unless the entries of the attention matrix are bounded or the matrix has low stable rank. We introduce two parameters which measure: (1) the max column norm in the normalized attention matrix, and (2) the ratio of row norms in the unnormalized attention matrix after detecting and removing large entries. We use these fine-grained parameters to capture the hardness of the problem. Despite previous lower bounds, we are able to achieve a linear time sampling algorithm even when the matrix has unbounded entries or a large stable rank, provided the above parameters are small. HyperAttention features a modular design that easily accommodates integration of other fast low-level implementations, particularly FlashAttention. Empirically, employing Locality Sensitive Hashing (LSH) to identify large entries, HyperAttention outperforms existing methods, giving significant speed improvements compared to state-of-the-art solutions like FlashAttention. We validate the empirical performance of HyperAttention on a variety of different long-context length datasets. For example, HyperAttention makes the inference time of ChatGLM2 50\% faster on 32k context length while perplexity increases from 5.6 to 6.3. On larger context length, e.g., 131k, with causal masking, HyperAttention offers 5-fold speedup on a single attention layer.

A Near-Linear Time Algorithm for the Chamfer Distance

For any two point sets $A,B \subset \mathbb{R}^d$ of size up to $n$, the Chamfer distance from $A$ to $B$ is defined as $\text{CH}(A,B)=\sum_{a \in A} \min_{b \in B} d_X(a,b)$, where $d_X$ is the underlying distance measure (e.g., the Euclidean or Manhattan distance). The Chamfer distance is a popular measure of dissimilarity between point clouds, used in many machine learning, computer vision, and graphics applications, and admits a straightforward $O(d n^2)$-time brute force algorithm. Further, the Chamfer distance is often used as a proxy for the more computationally demanding Earth-Mover (Optimal Transport) Distance. However, the \emph{quadratic} dependence on $n$ in the running time makes the naive approach intractable for large datasets. We overcome this bottleneck and present the first $(1+\epsilon)$-approximate algorithm for estimating the Chamfer distance with a near-linear running time. Specifically, our algorithm runs in time $O(nd \log (n)/\varepsilon^2)$ and is implementable. Our experiments demonstrate that it is both accurate and fast on large high-dimensional datasets. We believe that our algorithm will open new avenues for analyzing large high-dimensional point clouds. We also give evidence that if the goal is to \emph{report} a $(1+\varepsilon)$-approximate mapping from $A$ to $B$ (as opposed to just its value), then any sub-quadratic time algorithm is unlikely to exist.

Stars: Tera-Scale Graph Building for Clustering and Graph Learning

A fundamental procedure in the analysis of massive datasets is the construction of similarity graphs. Such graphs play a key role for many downstream tasks, including clustering, classification, graph learning, and nearest neighbor search. For these tasks, it is critical to build graphs which are sparse yet still representative of the underlying data. The benefits of sparsity are twofold: firstly, constructing dense graphs is infeasible in practice for large datasets, and secondly, the runtime of downstream tasks is directly influenced by the sparsity of the similarity graph. In this work, we present $\textit{Stars}$: a highly scalable method for building extremely sparse graphs via two-hop spanners, which are graphs where similar points are connected by a path of length at most two. Stars can construct two-hop spanners with significantly fewer similarity comparisons, which are a major bottleneck for learning based models where comparisons are expensive to evaluate. Theoretically, we demonstrate that Stars builds a graph in nearly-linear time, where approximate nearest neighbors are contained within two-hop neighborhoods. In practice, we have deployed Stars for multiple data sets allowing for graph building at the $\textit{Tera-Scale}$, i.e., for graphs with tens of trillions of edges. We evaluate the performance of Stars for clustering and graph learning, and demonstrate 10~1000-fold improvements in pairwise similarity comparisons compared to different baselines, and 2~10-fold improvement in running time without quality loss.

Learning and Testing Junta Distributions with Subcube Conditioning

We study the problems of learning and testing junta distributions on $\{-1,1\}^n$ with respect to the uniform distribution, where a distribution $p$ is a $k$-junta if its probability mass function $p(x)$ depends on a subset of at most $k$ variables. The main contribution is an algorithm for finding relevant coordinates in a $k$-junta distribution with subcube conditioning [BC18, CCKLW20]. We give two applications: 1. An algorithm for learning $k$-junta distributions with $\tilde{O}(k/\epsilon^2) \log n + O(2^k/\epsilon^2)$ subcube conditioning queries, and 2. An algorithm for testing $k$-junta distributions with $\tilde{O}((k + \sqrt{n})/\epsilon^2)$ subcube conditioning queries. All our algorithms are optimal up to poly-logarithmic factors. Our results show that subcube conditioning, as a natural model for accessing high-dimensional distributions, enables significant savings in learning and testing junta distributions compared to the standard sampling model. This addresses an open question posed by Aliakbarpour, Blais, and Rubinfeld [ABR17].

Optimal Sketching for Kronecker Product Regression and Low Rank Approximation

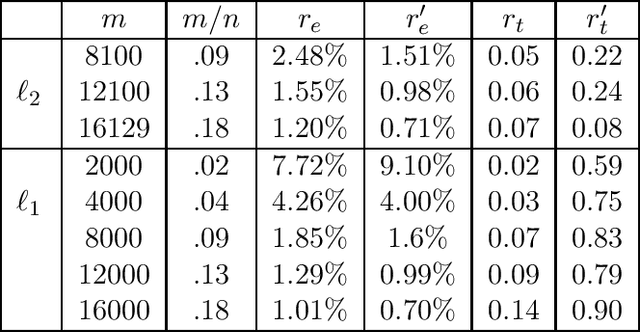
We study the Kronecker product regression problem, in which the design matrix is a Kronecker product of two or more matrices. Given $A_i \in \mathbb{R}^{n_i \times d_i}$ for $i=1,2,\dots,q$ where $n_i \gg d_i$ for each $i$, and $b \in \mathbb{R}^{n_1 n_2 \cdots n_q}$, let $\mathcal{A} = A_1 \otimes A_2 \otimes \cdots \otimes A_q$. Then for $p \in [1,2]$, the goal is to find $x \in \mathbb{R}^{d_1 \cdots d_q}$ that approximately minimizes $\|\mathcal{A}x - b\|_p$. Recently, Diao, Song, Sun, and Woodruff (AISTATS, 2018) gave an algorithm which is faster than forming the Kronecker product $\mathcal{A}$ Specifically, for $p=2$ their running time is $O(\sum_{i=1}^q \text{nnz}(A_i) + \text{nnz}(b))$, where nnz$(A_i)$ is the number of non-zero entries in $A_i$. Note that nnz$(b)$ can be as large as $n_1 \cdots n_q$. For $p=1,$ $q=2$ and $n_1 = n_2$, they achieve a worse bound of $O(n_1^{3/2} \text{poly}(d_1d_2) + \text{nnz}(b))$. In this work, we provide significantly faster algorithms. For $p=2$, our running time is $O(\sum_{i=1}^q \text{nnz}(A_i) )$, which has no dependence on nnz$(b)$. For $p<2$, our running time is $O(\sum_{i=1}^q \text{nnz}(A_i) + \text{nnz}(b))$, which matches the prior best running time for $p=2$. We also consider the related all-pairs regression problem, where given $A \in \mathbb{R}^{n \times d}, b \in \mathbb{R}^n$, we want to solve $\min_{x} \|\bar{A}x - \bar{b}\|_p$, where $\bar{A} \in \mathbb{R}^{n^2 \times d}, \bar{b} \in \mathbb{R}^{n^2}$ consist of all pairwise differences of the rows of $A,b$. We give an $O(\text{nnz}(A))$ time algorithm for $p \in[1,2]$, improving the $\Omega(n^2)$ time needed to form $\bar{A}$. Finally, we initiate the study of Kronecker product low rank and low $t$-rank approximation. For input $\mathcal{A}$ as above, we give $O(\sum_{i=1}^q \text{nnz}(A_i))$ time algorithms, which is much faster than computing $\mathcal{A}$.

Learning Two Layer Rectified Neural Networks in Polynomial Time

Consider the following fundamental learning problem: given input examples $x \in \mathbb{R}^d$ and their vector-valued labels, as defined by an underlying generative neural network, recover the weight matrices of this network. We consider two-layer networks, mapping $\mathbb{R}^d$ to $\mathbb{R}^m$, with $k$ non-linear activation units $f(\cdot)$, where $f(x) = \max \{x , 0\}$ is the ReLU. Such a network is specified by two weight matrices, $\mathbf{U}^* \in \mathbb{R}^{m \times k}, \mathbf{V}^* \in \mathbb{R}^{k \times d}$, such that the label of an example $x \in \mathbb{R}^{d}$ is given by $\mathbf{U}^* f(\mathbf{V}^* x)$, where $f(\cdot)$ is applied coordinate-wise. Given $n$ samples as a matrix $\mathbf{X} \in \mathbb{R}^{d \times n}$ and the (possibly noisy) labels $\mathbf{U}^* f(\mathbf{V}^* \mathbf{X}) + \mathbf{E}$ of the network on these samples, where $\mathbf{E}$ is a noise matrix, our goal is to recover the weight matrices $\mathbf{U}^*$ and $\mathbf{V}^*$. In this work, we develop algorithms and hardness results under varying assumptions on the input and noise. Although the problem is NP-hard even for $k=2$, by assuming Gaussian marginals over the input $\mathbf{X}$ we are able to develop polynomial time algorithms for the approximate recovery of $\mathbf{U}^*$ and $\mathbf{V}^*$. Perhaps surprisingly, in the noiseless case our algorithms recover $\mathbf{U}^*,\mathbf{V}^*$ exactly, i.e., with no error. To the best of the our knowledge, this is the first algorithm to accomplish exact recovery. For the noisy case, we give the first polynomial time algorithm that approximately recovers the weights in the presence of mean-zero noise $\mathbf{E}$. Our algorithms generalize to a larger class of rectified activation functions, $f(x) = 0$ when $x\leq 0$, and $f(x) > 0$ otherwise.