The ParClusterers Benchmark Suite (PCBS): A Fine-Grained Analysis of Scalable Graph Clustering

We introduce the ParClusterers Benchmark Suite (PCBS) -- a collection of highly scalable parallel graph clustering algorithms and benchmarking tools that streamline comparing different graph clustering algorithms and implementations. The benchmark includes clustering algorithms that target a wide range of modern clustering use cases, including community detection, classification, and dense subgraph mining. The benchmark toolkit makes it easy to run and evaluate multiple instances of different clustering algorithms, which can be useful for fine-tuning the performance of clustering on a given task, and for comparing different clustering algorithms based on different metrics of interest, including clustering quality and running time. Using PCBS, we evaluate a broad collection of real-world graph clustering datasets. Somewhat surprisingly, we find that the best quality results are obtained by algorithms that not included in many popular graph clustering toolkits. The PCBS provides a standardized way to evaluate and judge the quality-performance tradeoffs of the active research area of scalable graph clustering algorithms. We believe it will help enable fair, accurate, and nuanced evaluation of graph clustering algorithms in the future.

Results of the Big ANN: NeurIPS'23 competition

The 2023 Big ANN Challenge, held at NeurIPS 2023, focused on advancing the state-of-the-art in indexing data structures and search algorithms for practical variants of Approximate Nearest Neighbor (ANN) search that reflect the growing complexity and diversity of workloads. Unlike prior challenges that emphasized scaling up classical ANN search ~\cite{DBLP:conf/nips/SimhadriWADBBCH21}, this competition addressed filtered search, out-of-distribution data, sparse and streaming variants of ANNS. Participants developed and submitted innovative solutions that were evaluated on new standard datasets with constrained computational resources. The results showcased significant improvements in search accuracy and efficiency over industry-standard baselines, with notable contributions from both academic and industrial teams. This paper summarizes the competition tracks, datasets, evaluation metrics, and the innovative approaches of the top-performing submissions, providing insights into the current advancements and future directions in the field of approximate nearest neighbor search.

MUVERA: Multi-Vector Retrieval via Fixed Dimensional Encodings

Neural embedding models have become a fundamental component of modern information retrieval (IR) pipelines. These models produce a single embedding $x \in \mathbb{R}^d$ per data-point, allowing for fast retrieval via highly optimized maximum inner product search (MIPS) algorithms. Recently, beginning with the landmark ColBERT paper, multi-vector models, which produce a set of embedding per data point, have achieved markedly superior performance for IR tasks. Unfortunately, using these models for IR is computationally expensive due to the increased complexity of multi-vector retrieval and scoring. In this paper, we introduce MUVERA (MUlti-VEctor Retrieval Algorithm), a retrieval mechanism which reduces multi-vector similarity search to single-vector similarity search. This enables the usage of off-the-shelf MIPS solvers for multi-vector retrieval. MUVERA asymmetrically generates Fixed Dimensional Encodings (FDEs) of queries and documents, which are vectors whose inner product approximates multi-vector similarity. We prove that FDEs give high-quality $\epsilon$-approximations, thus providing the first single-vector proxy for multi-vector similarity with theoretical guarantees. Empirically, we find that FDEs achieve the same recall as prior state-of-the-art heuristics while retrieving 2-5$\times$ fewer candidates. Compared to prior state of the art implementations, MUVERA achieves consistently good end-to-end recall and latency across a diverse set of the BEIR retrieval datasets, achieving an average of 10$\%$ improved recall with $90\%$ lower latency.

Unleashing Graph Partitioning for Large-Scale Nearest Neighbor Search

We consider the fundamental problem of decomposing a large-scale approximate nearest neighbor search (ANNS) problem into smaller sub-problems. The goal is to partition the input points into neighborhood-preserving shards, so that the nearest neighbors of any point are contained in only a few shards. When a query arrives, a routing algorithm is used to identify the shards which should be searched for its nearest neighbors. This approach forms the backbone of distributed ANNS, where the dataset is so large that it must be split across multiple machines. In this paper, we design simple and highly efficient routing methods, and prove strong theoretical guarantees on their performance. A crucial characteristic of our routing algorithms is that they are inherently modular, and can be used with any partitioning method. This addresses a key drawback of prior approaches, where the routing algorithms are inextricably linked to their associated partitioning method. In particular, our new routing methods enable the use of balanced graph partitioning, which is a high-quality partitioning method without a naturally associated routing algorithm. Thus, we provide the first methods for routing using balanced graph partitioning that are extremely fast to train, admit low latency, and achieve high recall. We provide a comprehensive evaluation of our full partitioning and routing pipeline on billion-scale datasets, where it outperforms existing scalable partitioning methods by significant margins, achieving up to 2.14x higher QPS at 90% recall$@10$ than the best competitor.

Approximate Nearest Neighbor Search with Window Filters

We define and investigate the problem of $\textit{c-approximate window search}$: approximate nearest neighbor search where each point in the dataset has a numeric label, and the goal is to find nearest neighbors to queries within arbitrary label ranges. Many semantic search problems, such as image and document search with timestamp filters, or product search with cost filters, are natural examples of this problem. We propose and theoretically analyze a modular tree-based framework for transforming an index that solves the traditional c-approximate nearest neighbor problem into a data structure that solves window search. On standard nearest neighbor benchmark datasets equipped with random label values, adversarially constructed embeddings, and image search embeddings with real timestamps, we obtain up to a $75\times$ speedup over existing solutions at the same level of recall.

TeraHAC: Hierarchical Agglomerative Clustering of Trillion-Edge Graphs

We introduce TeraHAC, a $(1+\epsilon)$-approximate hierarchical agglomerative clustering (HAC) algorithm which scales to trillion-edge graphs. Our algorithm is based on a new approach to computing $(1+\epsilon)$-approximate HAC, which is a novel combination of the nearest-neighbor chain algorithm and the notion of $(1+\epsilon)$-approximate HAC. Our approach allows us to partition the graph among multiple machines and make significant progress in computing the clustering within each partition before any communication with other partitions is needed. We evaluate TeraHAC on a number of real-world and synthetic graphs of up to 8 trillion edges. We show that TeraHAC requires over 100x fewer rounds compared to previously known approaches for computing HAC. It is up to 8.3x faster than SCC, the state-of-the-art distributed algorithm for hierarchical clustering, while achieving 1.16x higher quality. In fact, TeraHAC essentially retains the quality of the celebrated HAC algorithm while significantly improving the running time.

Scaling Graph-Based ANNS Algorithms to Billion-Size Datasets: A Comparative Analysis

Algorithms for approximate nearest-neighbor search (ANNS) have been the topic of significant recent interest in the research community. However, evaluations of such algorithms are usually restricted to a small number of datasets with millions or tens of millions of points, whereas real-world applications require algorithms that work on the scale of billions of points. Furthermore, existing evaluations of ANNS algorithms are typically heavily focused on measuring and optimizing for queries-per second (QPS) at a given accuracy, which can be hardware-dependent and ignores important metrics such as build time. In this paper, we propose a set of principled measures for evaluating ANNS algorithms which refocuses on their scalability to billion-size datasets. These measures include ability to be efficiently parallelized, build times, and scaling relationships as dataset size increases. We also expand on the QPS measure with machine-agnostic measures such as the number of distance computations per query, and we evaluate ANNS data structures on their accuracy in more demanding settings required in modern applications, such as evaluating range queries and running on out-of-distribution data. We optimize four graph-based algorithms for the billion-scale setting, and in the process provide a general framework for making many incremental ANNS graph algorithms lock-free. We use our framework to evaluate the aforementioned graph-based ANNS algorithms as well as two alternative approaches.

Scalable Community Detection via Parallel Correlation Clustering

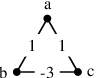
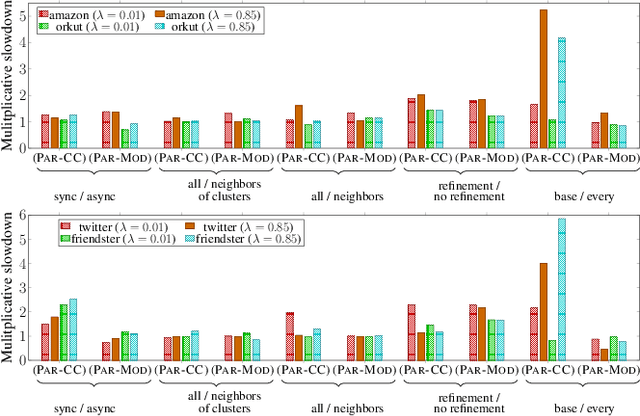
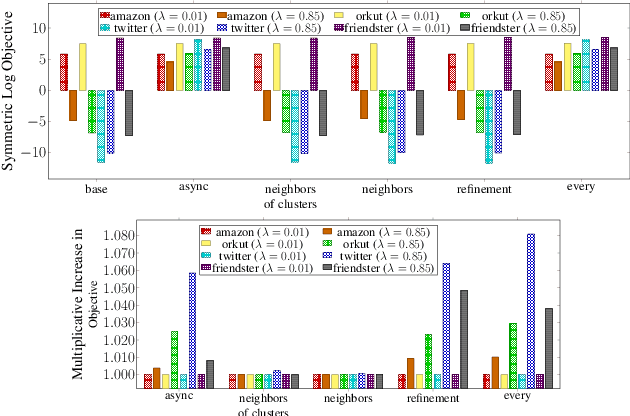
Graph clustering and community detection are central problems in modern data mining. The increasing need for analyzing billion-scale data calls for faster and more scalable algorithms for these problems. There are certain trade-offs between the quality and speed of such clustering algorithms. In this paper, we design scalable algorithms that achieve high quality when evaluated based on ground truth. We develop a generalized sequential and shared-memory parallel framework based on the LambdaCC objective (introduced by Veldt et al.), which encompasses modularity and correlation clustering. Our framework consists of highly-optimized implementations that scale to large data sets of billions of edges and that obtain high-quality clusters compared to ground-truth data, on both unweighted and weighted graphs. Our empirical evaluation shows that this framework improves the state-of-the-art trade-offs between speed and quality of scalable community detection. For example, on a 30-core machine with two-way hyper-threading, our implementations achieve orders of magnitude speedups over other correlation clustering baselines, and up to 28.44x speedups over our own sequential baselines while maintaining or improving quality.

Hierarchical Agglomerative Graph Clustering in Nearly-Linear Time

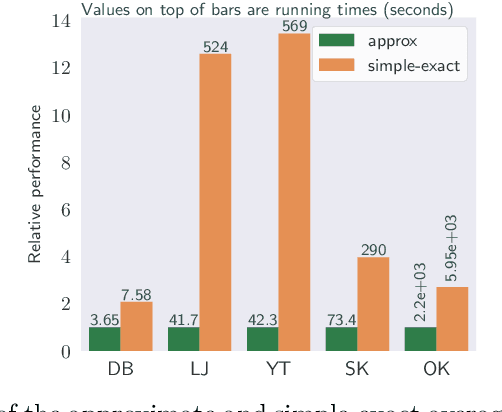
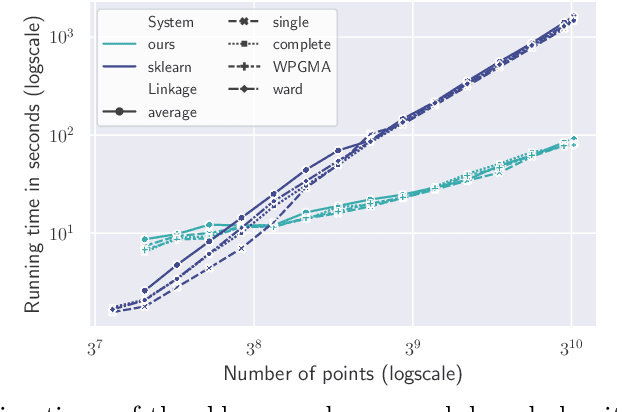
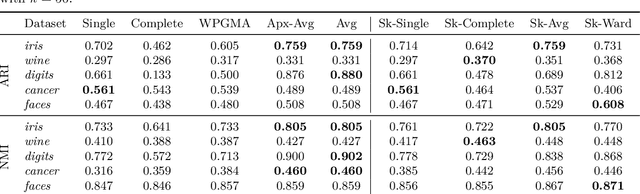
We study the widely used hierarchical agglomerative clustering (HAC) algorithm on edge-weighted graphs. We define an algorithmic framework for hierarchical agglomerative graph clustering that provides the first efficient $\tilde{O}(m)$ time exact algorithms for classic linkage measures, such as complete- and WPGMA-linkage, as well as other measures. Furthermore, for average-linkage, arguably the most popular variant of HAC, we provide an algorithm that runs in $\tilde{O}(n\sqrt{m})$ time. For this variant, this is the first exact algorithm that runs in subquadratic time, as long as $m=n^{2-\epsilon}$ for some constant $\epsilon > 0$. We complement this result with a simple $\epsilon$-close approximation algorithm for average-linkage in our framework that runs in $\tilde{O}(m)$ time. As an application of our algorithms, we consider clustering points in a metric space by first using $k$-NN to generate a graph from the point set, and then running our algorithms on the resulting weighted graph. We validate the performance of our algorithms on publicly available datasets, and show that our approach can speed up clustering of point datasets by a factor of 20.7--76.5x.

ParChain: A Framework for Parallel Hierarchical Agglomerative Clustering using Nearest-Neighbor Chain

This paper studies the hierarchical clustering problem, where the goal is to produce a dendrogram that represents clusters at varying scales of a data set. We propose the ParChain framework for designing parallel hierarchical agglomerative clustering (HAC) algorithms, and using the framework we obtain novel parallel algorithms for the complete linkage, average linkage, and Ward's linkage criteria. Compared to most previous parallel HAC algorithms, which require quadratic memory, our new algorithms require only linear memory, and are scalable to large data sets. ParChain is based on our parallelization of the nearest-neighbor chain algorithm, and enables multiple clusters to be merged on every round. We introduce two key optimizations that are critical for efficiency: a range query optimization that reduces the number of distance computations required when finding nearest neighbors of clusters, and a caching optimization that stores a subset of previously computed distances, which are likely to be reused. Experimentally, we show that our highly-optimized implementations using 48 cores with two-way hyper-threading achieve 5.8--110.1x speedup over state-of-the-art parallel HAC algorithms and achieve 13.75--54.23x self-relative speedup. Compared to state-of-the-art algorithms, our algorithms require up to 237.3x less space. Our algorithms are able to scale to data set sizes with tens of millions of points, which existing algorithms are not able to handle.