Best of Both Worlds in Online Control: Competitive Ratio and Policy Regret

We consider the fundamental problem of online control of a linear dynamical system from two different viewpoints: regret minimization and competitive analysis. We prove that the optimal competitive policy is well-approximated by a convex parameterized policy class, known as a disturbance-action control (DAC) policies. Using this structural result, we show that several recently proposed online control algorithms achieve the best of both worlds: sublinear regret vs. the best DAC policy selected in hindsight, and optimal competitive ratio, up to an additive correction which grows sublinearly in the time horizon. We further conclude that sublinear regret vs. the optimal competitive policy is attainable when the linear dynamical system is unknown, and even when a stabilizing controller for the dynamics is not available a priori.

Multi-User Reinforcement Learning with Low Rank Rewards

In this work, we consider the problem of collaborative multi-user reinforcement learning. In this setting there are multiple users with the same state-action space and transition probabilities but with different rewards. Under the assumption that the reward matrix of the $N$ users has a low-rank structure -- a standard and practically successful assumption in the offline collaborative filtering setting -- the question is can we design algorithms with significantly lower sample complexity compared to the ones that learn the MDP individually for each user. Our main contribution is an algorithm which explores rewards collaboratively with $N$ user-specific MDPs and can learn rewards efficiently in two key settings: tabular MDPs and linear MDPs. When $N$ is large and the rank is constant, the sample complexity per MDP depends logarithmically over the size of the state-space, which represents an exponential reduction (in the state-space size) when compared to the standard ``non-collaborative'' algorithms.

Adaptive Gradient Methods at the Edge of Stability

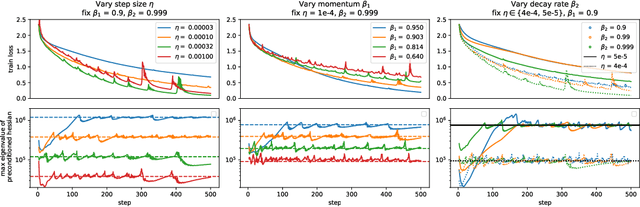
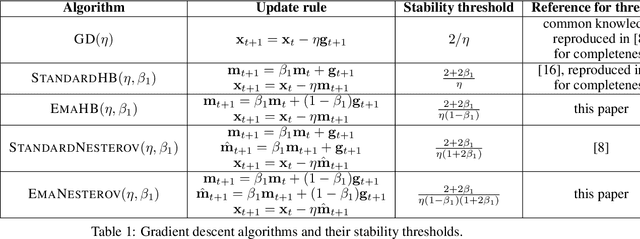
Very little is known about the training dynamics of adaptive gradient methods like Adam in deep learning. In this paper, we shed light on the behavior of these algorithms in the full-batch and sufficiently large batch settings. Specifically, we empirically demonstrate that during full-batch training, the maximum eigenvalue of the preconditioned Hessian typically equilibrates at a certain numerical value -- the stability threshold of a gradient descent algorithm. For Adam with step size $\eta$ and $\beta_1 = 0.9$, this stability threshold is $38/\eta$. Similar effects occur during minibatch training, especially as the batch size grows. Yet, even though adaptive methods train at the ``Adaptive Edge of Stability'' (AEoS), their behavior in this regime differs in a significant way from that of non-adaptive methods at the EoS. Whereas non-adaptive algorithms at the EoS are blocked from entering high-curvature regions of the loss landscape, adaptive gradient methods at the AEoS can keep advancing into high-curvature regions, while adapting the preconditioner to compensate. Our findings can serve as a foundation for the community's future understanding of adaptive gradient methods in deep learning.

Pushing the Efficiency-Regret Pareto Frontier for Online Learning of Portfolios and Quantum States

We revisit the classical online portfolio selection problem. It is widely assumed that a trade-off between computational complexity and regret is unavoidable, with Cover's Universal Portfolios algorithm, SOFT-BAYES and ADA-BARRONS currently constituting its state-of-the-art Pareto frontier. In this paper, we present the first efficient algorithm, BISONS, that obtains polylogarithmic regret with memory and per-step running time requirements that are polynomial in the dimension, displacing ADA-BARRONS from the Pareto frontier. Additionally, we resolve a COLT 2020 open problem by showing that a certain Follow-The-Regularized-Leader algorithm with log-barrier regularization suffers an exponentially larger dependence on the dimension than previously conjectured. Thus, we rule out this algorithm as a candidate for the Pareto frontier. We also extend our algorithm and analysis to a more general problem than online portfolio selection, viz. online learning of quantum states with log loss. This algorithm, called SCHRODINGER'S BISONS, is the first efficient algorithm with polylogarithmic regret for this more general problem.

Machine Learning for Mechanical Ventilation Control (Extended Abstract)

Mechanical ventilation is one of the most widely used therapies in the ICU. However, despite broad application from anaesthesia to COVID-related life support, many injurious challenges remain. We frame these as a control problem: ventilators must let air in and out of the patient's lungs according to a prescribed trajectory of airway pressure. Industry-standard controllers, based on the PID method, are neither optimal nor robust. Our data-driven approach learns to control an invasive ventilator by training on a simulator itself trained on data collected from the ventilator. This method outperforms popular reinforcement learning algorithms and even controls the physical ventilator more accurately and robustly than PID. These results underscore how effective data-driven methodologies can be for invasive ventilation and suggest that more general forms of ventilation (e.g., non-invasive, adaptive) may also be amenable.

The Skellam Mechanism for Differentially Private Federated Learning

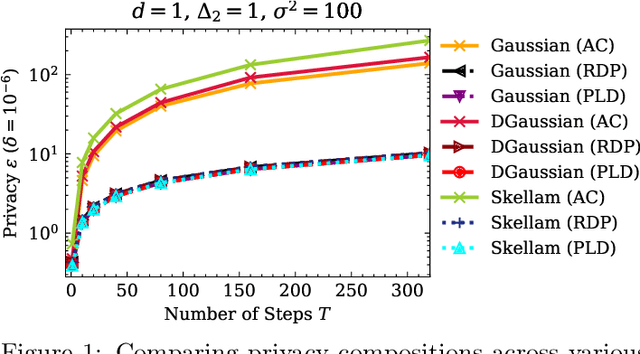
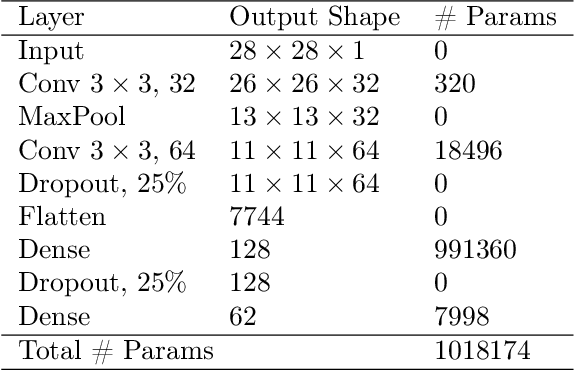
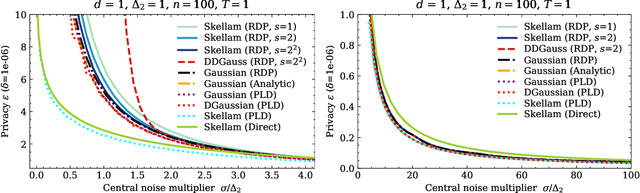
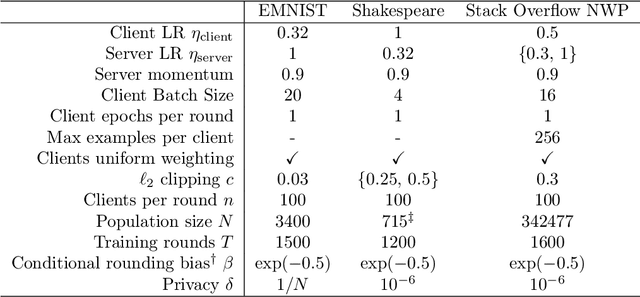
We introduce the multi-dimensional Skellam mechanism, a discrete differential privacy mechanism based on the difference of two independent Poisson random variables. To quantify its privacy guarantees, we analyze the privacy loss distribution via a numerical evaluation and provide a sharp bound on the R\'enyi divergence between two shifted Skellam distributions. While useful in both centralized and distributed privacy applications, we investigate how it can be applied in the context of federated learning with secure aggregation under communication constraints. Our theoretical findings and extensive experimental evaluations demonstrate that the Skellam mechanism provides the same privacy-accuracy trade-offs as the continuous Gaussian mechanism, even when the precision is low. More importantly, Skellam is closed under summation and sampling from it only requires sampling from a Poisson distribution -- an efficient routine that ships with all machine learning and data analysis software packages. These features, along with its discrete nature and competitive privacy-accuracy trade-offs, make it an attractive practical alternative to the newly introduced discrete Gaussian mechanism.

Online Target Q-learning with Reverse Experience Replay: Efficiently finding the Optimal Policy for Linear MDPs

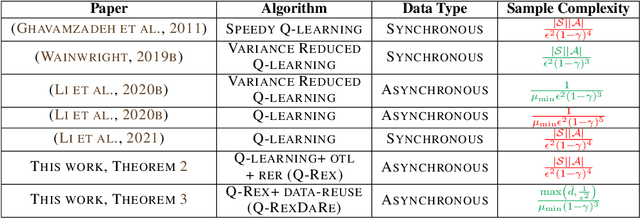
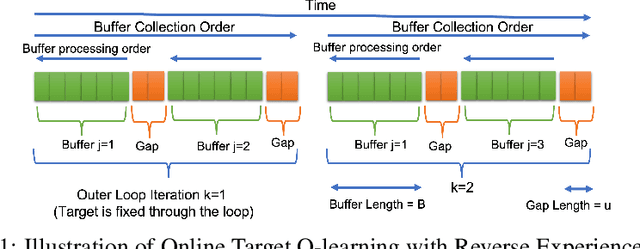
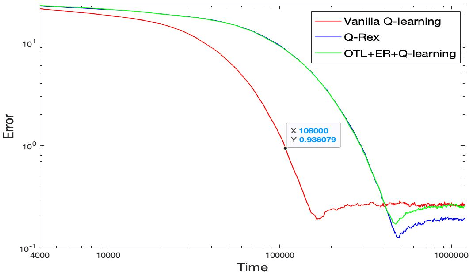
Q-learning is a popular Reinforcement Learning (RL) algorithm which is widely used in practice with function approximation (Mnih et al., 2015). In contrast, existing theoretical results are pessimistic about Q-learning. For example, (Baird, 1995) shows that Q-learning does not converge even with linear function approximation for linear MDPs. Furthermore, even for tabular MDPs with synchronous updates, Q-learning was shown to have sub-optimal sample complexity (Li et al., 2021;Azar et al., 2013). The goal of this work is to bridge the gap between practical success of Q-learning and the relatively pessimistic theoretical results. The starting point of our work is the observation that in practice, Q-learning is used with two important modifications: (i) training with two networks, called online network and target network simultaneously (online target learning, or OTL) , and (ii) experience replay (ER) (Mnih et al., 2015). While they have been observed to play a significant role in the practical success of Q-learning, a thorough theoretical understanding of how these two modifications improve the convergence behavior of Q-learning has been missing in literature. By carefully combining Q-learning with OTL and reverse experience replay (RER) (a form of experience replay), we present novel methods Q-Rex and Q-RexDaRe (Q-Rex + data reuse). We show that Q-Rex efficiently finds the optimal policy for linear MDPs (or more generally for MDPs with zero inherent Bellman error with linear approximation (ZIBEL)) and provide non-asymptotic bounds on sample complexity -- the first such result for a Q-learning method for this class of MDPs under standard assumptions. Furthermore, we demonstrate that Q-RexDaRe in fact achieves near optimal sample complexity in the tabular setting, improving upon the existing results for vanilla Q-learning.

Efficient Methods for Online Multiclass Logistic Regression

Multiclass logistic regression is a fundamental task in machine learning with applications in classification and boosting. Previous work (Foster et al., 2018) has highlighted the importance of improper predictors for achieving "fast rates" in the online multiclass logistic regression problem without suffering exponentially from secondary problem parameters, such as the norm of the predictors in the comparison class. While Foster et al. (2018) introduced a statistically optimal algorithm, it is in practice computationally intractable due to its run-time complexity being a large polynomial in the time horizon and dimension of input feature vectors. In this paper, we develop a new algorithm, FOLKLORE, for the problem which runs significantly faster than the algorithm of Foster et al.(2018) -- the running time per iteration scales quadratically in the dimension -- at the cost of a linear dependence on the norm of the predictors in the regret bound. This yields the first practical algorithm for online multiclass logistic regression, resolving an open problem of Foster et al.(2018). Furthermore, we show that our algorithm can be applied to online bandit multiclass prediction and online multiclass boosting, yielding more practical algorithms for both problems compared to the ones in Foster et al.(2018) with similar performance guarantees. Finally, we also provide an online-to-batch conversion result for our algorithm.

Acceleration via Fractal Learning Rate Schedules

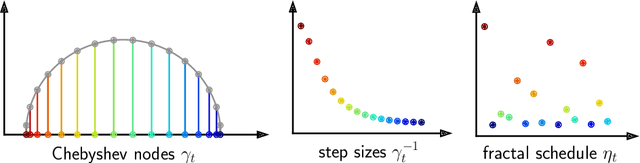
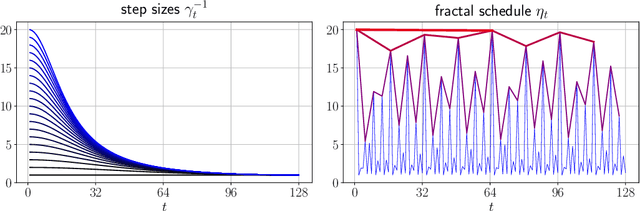
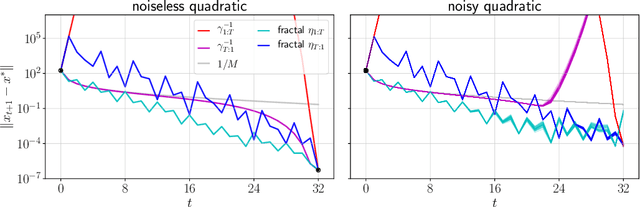
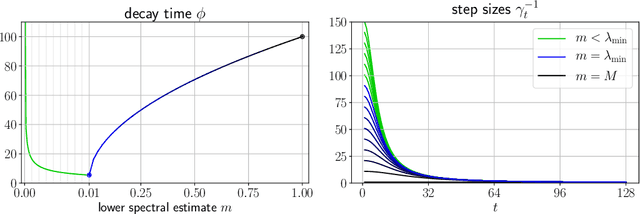
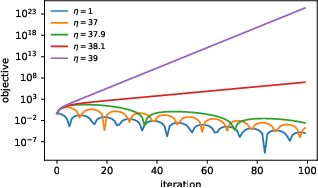
When balancing the practical tradeoffs of iterative methods for large-scale optimization, the learning rate schedule remains notoriously difficult to understand and expensive to tune. We demonstrate the presence of these subtleties even in the innocuous case when the objective is a convex quadratic. We reinterpret an iterative algorithm from the numerical analysis literature as what we call the Chebyshev learning rate schedule for accelerating vanilla gradient descent, and show that the problem of mitigating instability leads to a fractal ordering of step sizes. We provide some experiments and discussion to challenge current understandings of the "edge of stability" in deep learning: even in simple settings, provable acceleration can be obtained by making negative local progress on the objective.

Machine Learning for Mechanical Ventilation Control

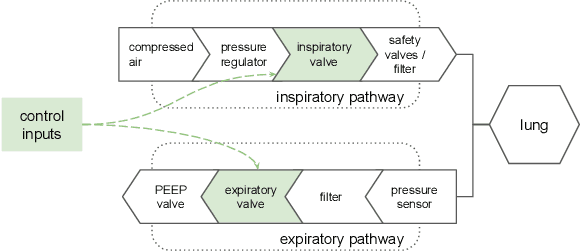
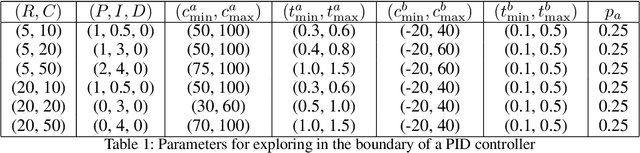
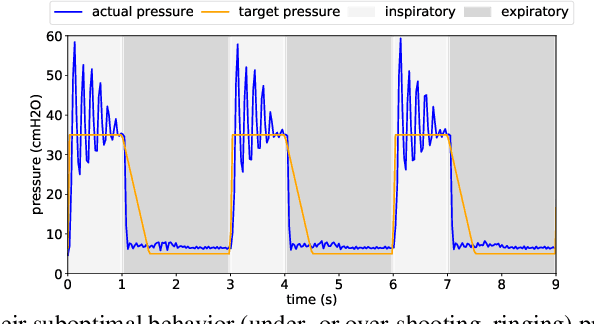
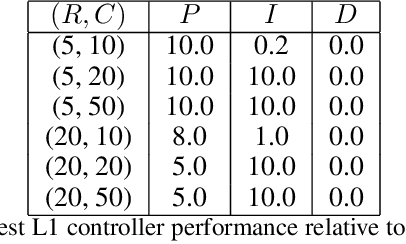
We consider the problem of controlling an invasive mechanical ventilator for pressure-controlled ventilation: a controller must let air in and out of a sedated patient's lungs according to a trajectory of airway pressures specified by a clinician. Hand-tuned PID controllers and similar variants have comprised the industry standard for decades, yet can behave poorly by over- or under-shooting their target or oscillating rapidly. We consider a data-driven machine learning approach: First, we train a simulator based on data we collect from an artificial lung. Then, we train deep neural network controllers on these simulators.We show that our controllers are able to track target pressure waveforms significantly better than PID controllers. We further show that a learned controller generalizes across lungs with varying characteristics much more readily than PID controllers do.