Understanding Optimization in Deep Learning with Central Flows

Optimization in deep learning remains poorly understood, even in the simple setting of deterministic (i.e. full-batch) training. A key difficulty is that much of an optimizer's behavior is implicitly determined by complex oscillatory dynamics, referred to as the "edge of stability." The main contribution of this paper is to show that an optimizer's implicit behavior can be explicitly captured by a "central flow:" a differential equation which models the time-averaged optimization trajectory. We show that these flows can empirically predict long-term optimization trajectories of generic neural networks with a high degree of numerical accuracy. By interpreting these flows, we reveal for the first time 1) the precise sense in which RMSProp adapts to the local loss landscape, and 2) an "acceleration via regularization" mechanism, wherein adaptive optimizers implicitly navigate towards low-curvature regions in which they can take larger steps. This mechanism is key to the efficacy of these adaptive optimizers. Overall, we believe that central flows constitute a promising tool for reasoning about optimization in deep learning.

Adaptive Gradient Methods at the Edge of Stability

Very little is known about the training dynamics of adaptive gradient methods like Adam in deep learning. In this paper, we shed light on the behavior of these algorithms in the full-batch and sufficiently large batch settings. Specifically, we empirically demonstrate that during full-batch training, the maximum eigenvalue of the preconditioned Hessian typically equilibrates at a certain numerical value -- the stability threshold of a gradient descent algorithm. For Adam with step size $\eta$ and $\beta_1 = 0.9$, this stability threshold is $38/\eta$. Similar effects occur during minibatch training, especially as the batch size grows. Yet, even though adaptive methods train at the ``Adaptive Edge of Stability'' (AEoS), their behavior in this regime differs in a significant way from that of non-adaptive methods at the EoS. Whereas non-adaptive algorithms at the EoS are blocked from entering high-curvature regions of the loss landscape, adaptive gradient methods at the AEoS can keep advancing into high-curvature regions, while adapting the preconditioner to compensate. Our findings can serve as a foundation for the community's future understanding of adaptive gradient methods in deep learning.

Gradient Descent on Neural Networks Typically Occurs at the Edge of Stability

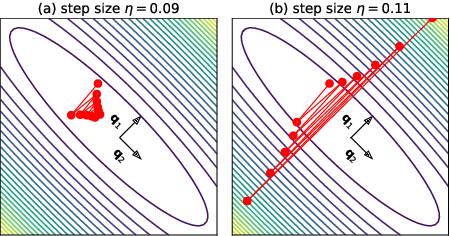
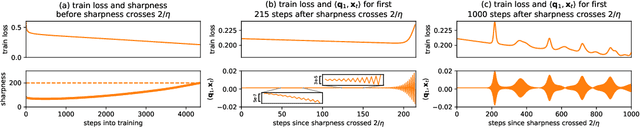
We empirically demonstrate that full-batch gradient descent on neural network training objectives typically operates in a regime we call the Edge of Stability. In this regime, the maximum eigenvalue of the training loss Hessian hovers just above the numerical value $2 / \text{(step size)}$, and the training loss behaves non-monotonically over short timescales, yet consistently decreases over long timescales. Since this behavior is inconsistent with several widespread presumptions in the field of optimization, our findings raise questions as to whether these presumptions are relevant to neural network training. We hope that our findings will inspire future efforts aimed at rigorously understanding optimization at the Edge of Stability. Code is available at https://github.com/locuslab/edge-of-stability.