Spark Transformer: Reactivating Sparsity in FFN and Attention

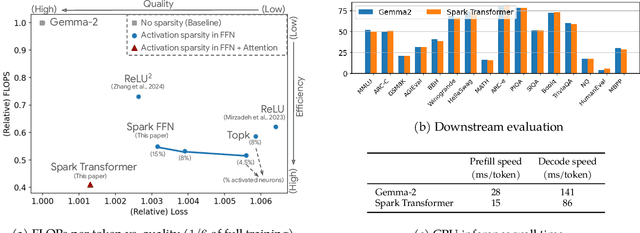
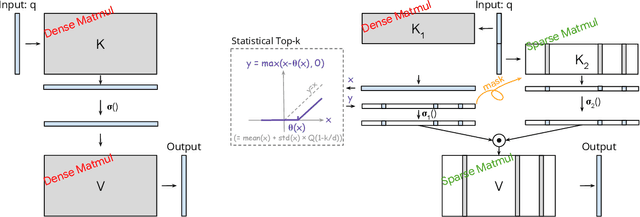
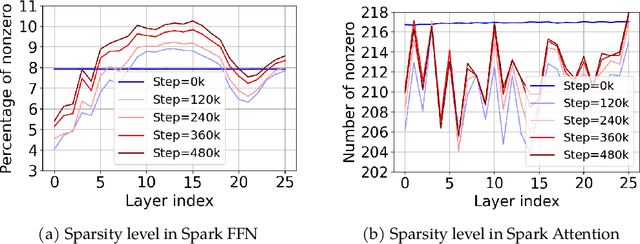
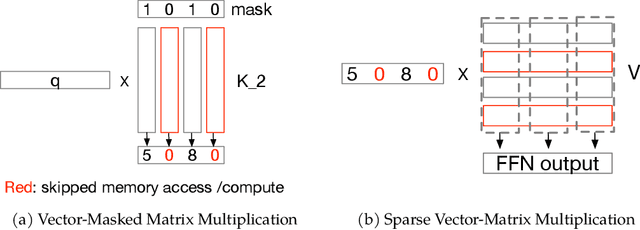
The discovery of the lazy neuron phenomenon in trained Transformers, where the vast majority of neurons in their feed-forward networks (FFN) are inactive for each token, has spurred tremendous interests in activation sparsity for enhancing large model efficiency. While notable progress has been made in translating such sparsity to wall-time benefits, modern Transformers have moved away from the ReLU activation function crucial to this phenomenon. Existing efforts on re-introducing activation sparsity often degrade model quality, increase parameter count, complicate or slow down training. Sparse attention, the application of sparse activation to the attention mechanism, often faces similar challenges. This paper introduces the Spark Transformer, a novel architecture that achieves a high level of activation sparsity in both FFN and the attention mechanism while maintaining model quality, parameter count, and standard training procedures. Our method realizes sparsity via top-k masking for explicit control over sparsity level. Crucially, we introduce statistical top-k, a hardware-accelerator-friendly, linear-time approximate algorithm that avoids costly sorting and mitigates significant training slowdown from standard top-$k$ operators. Furthermore, Spark Transformer reallocates existing FFN parameters and attention key embeddings to form a low-cost predictor for identifying activated entries. This design not only mitigates quality loss from enforced sparsity, but also enhances wall-time benefit. Pretrained with the Gemma-2 recipe, Spark Transformer demonstrates competitive performance on standard benchmarks while exhibiting significant sparsity: only 8% of FFN neurons are activated, and each token attends to a maximum of 256 tokens. This sparsity translates to a 2.5x reduction in FLOPs, leading to decoding wall-time speedups of up to 1.79x on CPU and 1.40x on GPU.

Faster Approx. Top-K: Harnessing the Full Power of Two Stages

We consider the Top-$K$ selection problem, which aims to identify the largest-$K$ elements from an array. Top-$K$ selection arises in many machine learning algorithms and often becomes a bottleneck on accelerators, which are optimized for dense matrix multiplications. To address this problem, \citet{chern2022tpuknnknearestneighbor} proposed a fast two-stage \textit{approximate} Top-$K$ algorithm: (i) partition the input array and select the top-$1$ element from each partition, (ii) sort this \textit{smaller subset} and return the top $K$ elements. In this paper, we consider a generalized version of this algorithm, where the first stage selects top-$K'$ elements, for some $1 \leq K' \leq K$, from each partition. Our contributions are as follows: (i) we derive an expression for the expected recall of this generalized algorithm and show that choosing $K' > 1$ with fewer partitions in the first stage reduces the input size to the second stage more effectively while maintaining the same expected recall as the original algorithm, (ii) we derive a bound on the expected recall for the original algorithm in \citet{chern2022tpuknnknearestneighbor} that is provably tighter by a factor of $2$ than the one in that paper, and (iii) we implement our algorithm on Cloud TPUv5e and achieve around an order of magnitude speedups over the original algorithm without sacrificing recall on real-world tasks.

HiRE: High Recall Approximate Top-$k$ Estimation for Efficient LLM Inference

Autoregressive decoding with generative Large Language Models (LLMs) on accelerators (GPUs/TPUs) is often memory-bound where most of the time is spent on transferring model parameters from high bandwidth memory (HBM) to cache. On the other hand, recent works show that LLMs can maintain quality with significant sparsity/redundancy in the feedforward (FFN) layers by appropriately training the model to operate on a top-$k$ fraction of rows/columns (where $k \approx 0.05$), there by suggesting a way to reduce the transfer of model parameters, and hence latency. However, exploiting this sparsity for improving latency is hindered by the fact that identifying top rows/columns is data-dependent and is usually performed using full matrix operations, severely limiting potential gains. To address these issues, we introduce HiRE (High Recall Approximate Top-k Estimation). HiRE comprises of two novel components: (i) a compression scheme to cheaply predict top-$k$ rows/columns with high recall, followed by full computation restricted to the predicted subset, and (ii) DA-TOP-$k$: an efficient multi-device approximate top-$k$ operator. We demonstrate that on a one billion parameter model, HiRE applied to both the softmax as well as feedforward layers, achieves almost matching pretraining and downstream accuracy, and speeds up inference latency by $1.47\times$ on a single TPUv5e device.

Second Order Methods for Bandit Optimization and Control

Bandit convex optimization (BCO) is a general framework for online decision making under uncertainty. While tight regret bounds for general convex losses have been established, existing algorithms achieving these bounds have prohibitive computational costs for high dimensional data. In this paper, we propose a simple and practical BCO algorithm inspired by the online Newton step algorithm. We show that our algorithm achieves optimal (in terms of horizon) regret bounds for a large class of convex functions that we call $\kappa$-convex. This class contains a wide range of practically relevant loss functions including linear, quadratic, and generalized linear models. In addition to optimal regret, this method is the most efficient known algorithm for several well-studied applications including bandit logistic regression. Furthermore, we investigate the adaptation of our second-order bandit algorithm to online convex optimization with memory. We show that for loss functions with a certain affine structure, the extended algorithm attains optimal regret. This leads to an algorithm with optimal regret for bandit LQR/LQG problems under a fully adversarial noise model, thereby resolving an open question posed in \citep{gradu2020non} and \citep{sun2023optimal}. Finally, we show that the more general problem of BCO with (non-affine) memory is harder. We derive a $\tilde{\Omega}(T^{2/3})$ regret lower bound, even under the assumption of smooth and quadratic losses.

Tandem Transformers for Inference Efficient LLMs

The autoregressive nature of conventional large language models (LLMs) inherently limits inference speed, as tokens are generated sequentially. While speculative and parallel decoding techniques attempt to mitigate this, they face limitations: either relying on less accurate smaller models for generation or failing to fully leverage the base LLM's representations. We introduce a novel architecture, Tandem transformers, to address these issues. This architecture uniquely combines (1) a small autoregressive model and (2) a large model operating in block mode (processing multiple tokens simultaneously). The small model's predictive accuracy is substantially enhanced by granting it attention to the large model's richer representations. On the PaLM2 pretraining dataset, a tandem of PaLM2-Bison and PaLM2-Gecko demonstrates a 3.3% improvement in next-token prediction accuracy over a standalone PaLM2-Gecko, offering a 1.16x speedup compared to a PaLM2-Otter model with comparable downstream performance. We further incorporate the tandem model within the speculative decoding (SPEED) framework where the large model validates tokens from the small model. This ensures that the Tandem of PaLM2-Bison and PaLM2-Gecko achieves substantial speedup (around 1.14x faster than using vanilla PaLM2-Gecko in SPEED) while maintaining identical downstream task accuracy.

Steering Deep Feature Learning with Backward Aligned Feature Updates

Deep learning succeeds by doing hierarchical feature learning, yet tuning Hyper-Parameters (HP) such as initialization scales, learning rates etc., only give indirect control over this behavior. In this paper, we propose the alignment between the feature updates and the backward pass as a key notion to predict, measure and control feature learning. On the one hand, we show that when alignment holds, the magnitude of feature updates after one SGD step is related to the magnitude of the forward and backward passes by a simple and general formula. This leads to techniques to automatically adjust HPs (initialization scales and learning rates) at initialization and throughout training to attain a desired feature learning behavior. On the other hand, we show that, at random initialization, this alignment is determined by the spectrum of a certain kernel, and that well-conditioned layer-to-layer Jacobians (aka dynamical isometry) implies alignment. Finally, we investigate ReLU MLPs and ResNets in the large width-then-depth limit. Combining hints from random matrix theory and numerical experiments, we show that (i) in MLP with iid initializations, alignment degenerates with depth, making it impossible to start training, and that (ii) in ResNets, the branch scale $1/\sqrt{\text{depth}}$ is the only one maintaining non-trivial alignment at infinite depth.

Near Optimal Heteroscedastic Regression with Symbiotic Learning

We consider the problem of heteroscedastic linear regression, where, given $n$ samples $(\mathbf{x}_i, y_i)$ from $y_i = \langle \mathbf{w}^{*}, \mathbf{x}_i \rangle + \epsilon_i \cdot \langle \mathbf{f}^{*}, \mathbf{x}_i \rangle$ with $\mathbf{x}_i \sim N(0,\mathbf{I})$, $\epsilon_i \sim N(0,1)$, we aim to estimate $\mathbf{w}^{*}$. Beyond classical applications of such models in statistics, econometrics, time series analysis etc., it is also particularly relevant in machine learning when data is collected from multiple sources of varying but apriori unknown quality. Our work shows that we can estimate $\mathbf{w}^{*}$ in squared norm up to an error of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2 \cdot \left(\frac{1}{n} + \left(\frac{d}{n}\right)^2\right)\right)$ and prove a matching lower bound (upto log factors). This represents a substantial improvement upon the previous best known upper bound of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2\cdot \frac{d}{n}\right)$. Our algorithm is an alternating minimization procedure with two key subroutines 1. An adaptation of the classical weighted least squares heuristic to estimate $\mathbf{w}^{*}$, for which we provide the first non-asymptotic guarantee. 2. A nonconvex pseudogradient descent procedure for estimating $\mathbf{f}^{*}$ inspired by phase retrieval. As corollaries, we obtain fast non-asymptotic rates for two important problems, linear regression with multiplicative noise and phase retrieval with multiplicative noise, both of which are of independent interest. Beyond this, the proof of our lower bound, which involves a novel adaptation of LeCam's method for handling infinite mutual information quantities (thereby preventing a direct application of standard techniques like Fano's method), could also be of broader interest for establishing lower bounds for other heteroscedastic or heavy-tailed statistical problems.

Simplicity Bias in 1-Hidden Layer Neural Networks

Recent works have demonstrated that neural networks exhibit extreme simplicity bias(SB). That is, they learn only the simplest features to solve a task at hand, even in the presence of other, more robust but more complex features. Due to the lack of a general and rigorous definition of features, these works showcase SB on semi-synthetic datasets such as Color-MNIST, MNIST-CIFAR where defining features is relatively easier. In this work, we rigorously define as well as thoroughly establish SB for one hidden layer neural networks. More concretely, (i) we define SB as the network essentially being a function of a low dimensional projection of the inputs (ii) theoretically, we show that when the data is linearly separable, the network primarily depends on only the linearly separable ($1$-dimensional) subspace even in the presence of an arbitrarily large number of other, more complex features which could have led to a significantly more robust classifier, (iii) empirically, we show that models trained on real datasets such as Imagenette and Waterbirds-Landbirds indeed depend on a low dimensional projection of the inputs, thereby demonstrating SB on these datasets, iv) finally, we present a natural ensemble approach that encourages diversity in models by training successive models on features not used by earlier models, and demonstrate that it yields models that are significantly more robust to Gaussian noise.

Consistent Multiclass Algorithms for Complex Metrics and Constraints

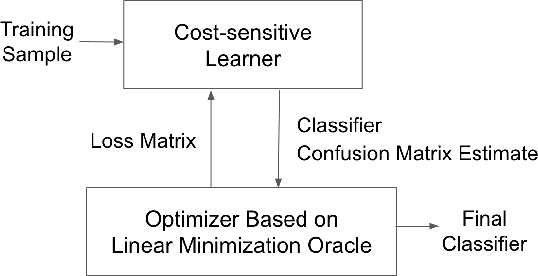
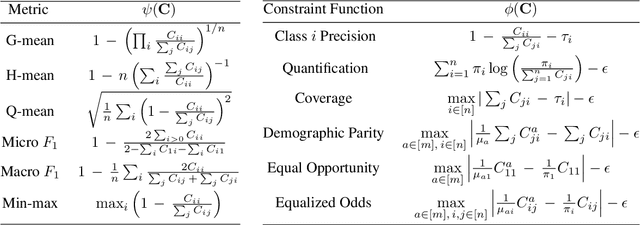
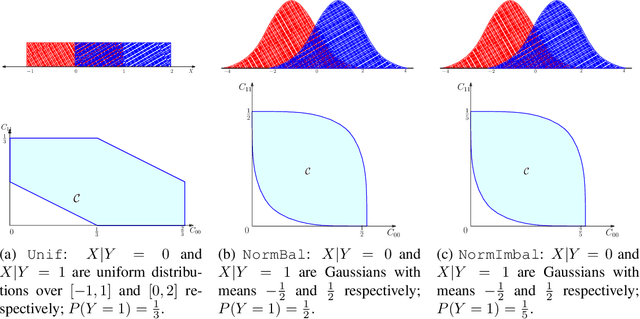
We present consistent algorithms for multiclass learning with complex performance metrics and constraints, where the objective and constraints are defined by arbitrary functions of the confusion matrix. This setting includes many common performance metrics such as the multiclass G-mean and micro F1-measure, and constraints such as those on the classifier's precision and recall and more recent measures of fairness discrepancy. We give a general framework for designing consistent algorithms for such complex design goals by viewing the learning problem as an optimization problem over the set of feasible confusion matrices. We provide multiple instantiations of our framework under different assumptions on the performance metrics and constraints, and in each case show rates of convergence to the optimal (feasible) classifier (and thus asymptotic consistency). Experiments on a variety of multiclass classification tasks and fairness-constrained problems show that our algorithms compare favorably to the state-of-the-art baselines.

Multi-User Reinforcement Learning with Low Rank Rewards

In this work, we consider the problem of collaborative multi-user reinforcement learning. In this setting there are multiple users with the same state-action space and transition probabilities but with different rewards. Under the assumption that the reward matrix of the $N$ users has a low-rank structure -- a standard and practically successful assumption in the offline collaborative filtering setting -- the question is can we design algorithms with significantly lower sample complexity compared to the ones that learn the MDP individually for each user. Our main contribution is an algorithm which explores rewards collaboratively with $N$ user-specific MDPs and can learn rewards efficiently in two key settings: tabular MDPs and linear MDPs. When $N$ is large and the rank is constant, the sample complexity per MDP depends logarithmically over the size of the state-space, which represents an exponential reduction (in the state-space size) when compared to the standard ``non-collaborative'' algorithms.