Can a Transformer Represent a Kalman Filter?

Transformers are a class of autoregressive deep learning architectures which have recently achieved state-of-the-art performance in various vision, language, and robotics tasks. We revisit the problem of Kalman Filtering in linear dynamical systems and show that Transformers can approximate the Kalman Filter in a strong sense. Specifically, for any observable LTI system we construct an explicit causally-masked Transformer which implements the Kalman Filter, up to a small additive error which is bounded uniformly in time; we call our construction the Transformer Filter. Our construction is based on a two-step reduction. We first show that a softmax self-attention block can exactly represent a certain Gaussian kernel smoothing estimator. We then show that this estimator closely approximates the Kalman Filter. We also investigate how the Transformer Filter can be used for measurement-feedback control and prove that the resulting nonlinear controllers closely approximate the performance of standard optimal control policies such as the LQG controller.

Best of Both Worlds in Online Control: Competitive Ratio and Policy Regret

We consider the fundamental problem of online control of a linear dynamical system from two different viewpoints: regret minimization and competitive analysis. We prove that the optimal competitive policy is well-approximated by a convex parameterized policy class, known as a disturbance-action control (DAC) policies. Using this structural result, we show that several recently proposed online control algorithms achieve the best of both worlds: sublinear regret vs. the best DAC policy selected in hindsight, and optimal competitive ratio, up to an additive correction which grows sublinearly in the time horizon. We further conclude that sublinear regret vs. the optimal competitive policy is attainable when the linear dynamical system is unknown, and even when a stabilizing controller for the dynamics is not available a priori.

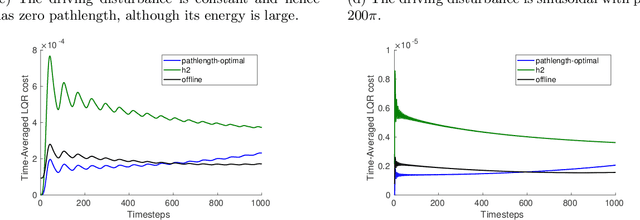
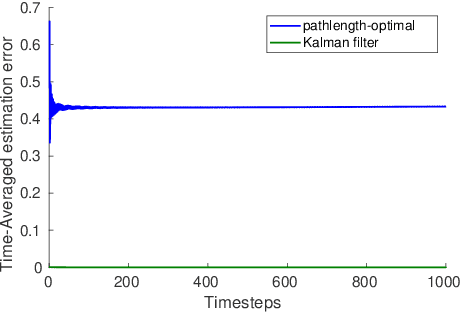
Online estimation and control with optimal pathlength regret

A natural goal when designing online learning algorithms for non-stationary environments is to bound the regret of the algorithm in terms of the temporal variation of the input sequence. Intuitively, when the variation is small, it should be easier for the algorithm to achieve low regret, since past observations are predictive of future inputs. Such data-dependent "pathlength" regret bounds have recently been obtained for a wide variety of online learning problems, including OCO and bandits. We obtain the first pathlength regret bounds for online control and estimation (e.g. Kalman filtering) in linear dynamical systems. The key idea in our derivation is to reduce pathlength-optimal filtering and control to certain variational problems in robust estimation and control; these reductions may be of independent interest. Numerical simulations confirm that our pathlength-optimal algorithms outperform traditional $H_2$ and $H_{\infty}$ algorithms when the environment varies over time.

Competitive Control

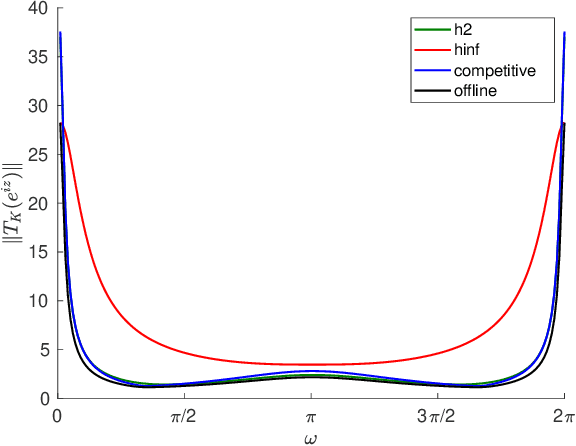
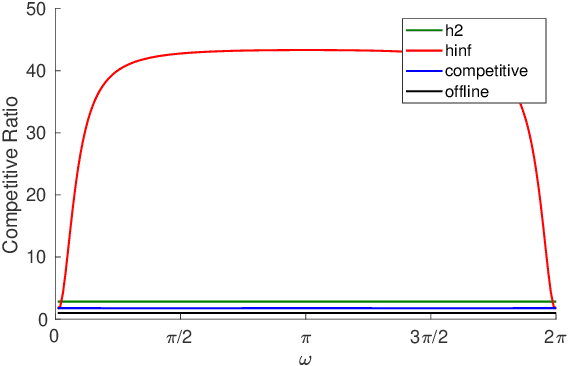
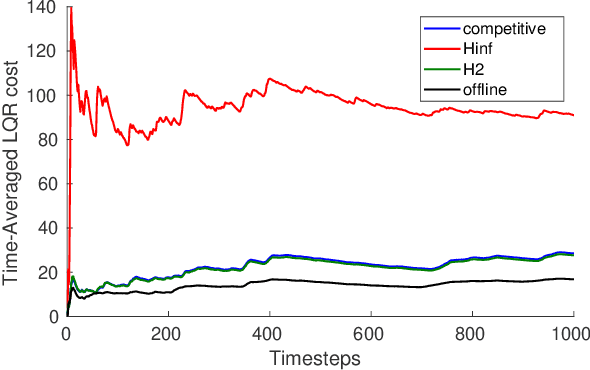
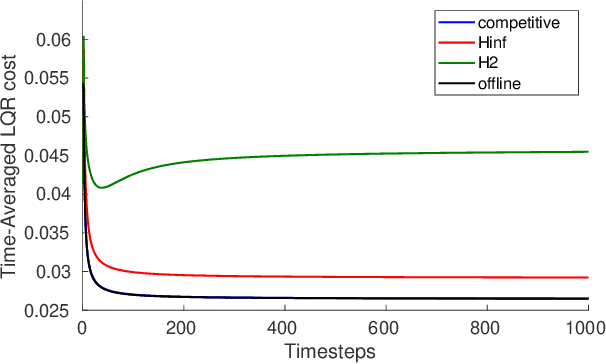
We consider control from the perspective of competitive analysis. Unlike much prior work on learning-based control, which focuses on minimizing regret against the best controller selected in hindsight from some specific class, we focus on designing an online controller which competes against a clairvoyant offline optimal controller. A natural performance metric in this setting is competitive ratio, which is the ratio between the cost incurred by the online controller and the cost incurred by the offline optimal controller. Using operator-theoretic techniques from robust control, we derive a computationally efficient state-space description of the the controller with optimal competitive ratio in both finite-horizon and infinite-horizon settings. We extend competitive control to nonlinear systems using Model Predictive Control (MPC) and present numerical experiments which show that our competitive controller can significantly outperform standard $H_2$ and $H_{\infty}$ controllers in the MPC setting.

Regret-optimal Estimation and Control

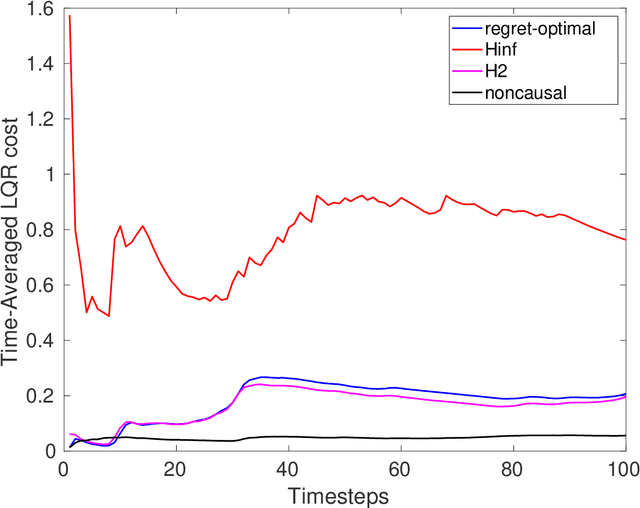
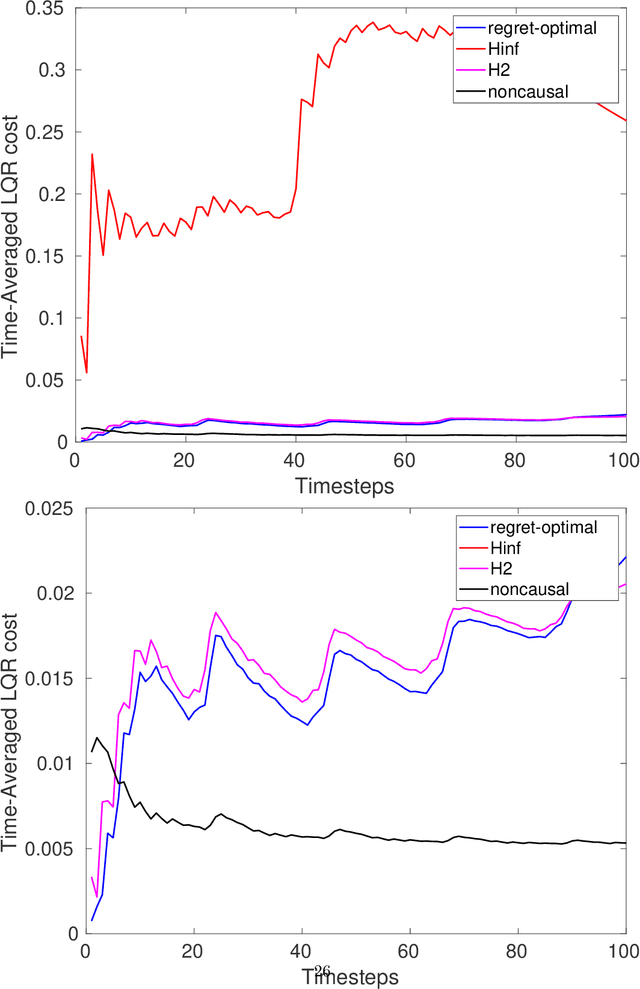
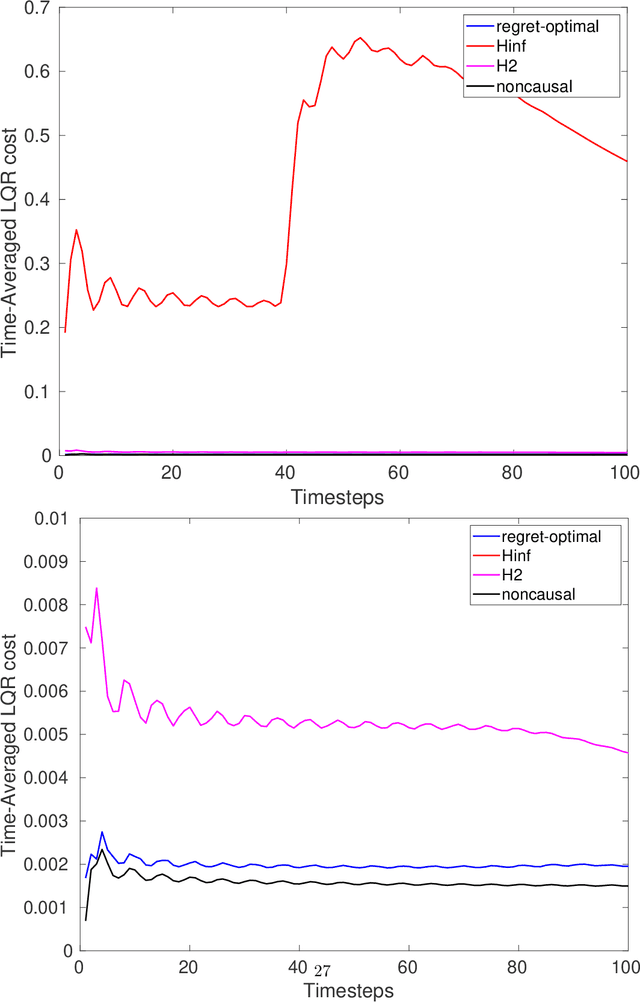
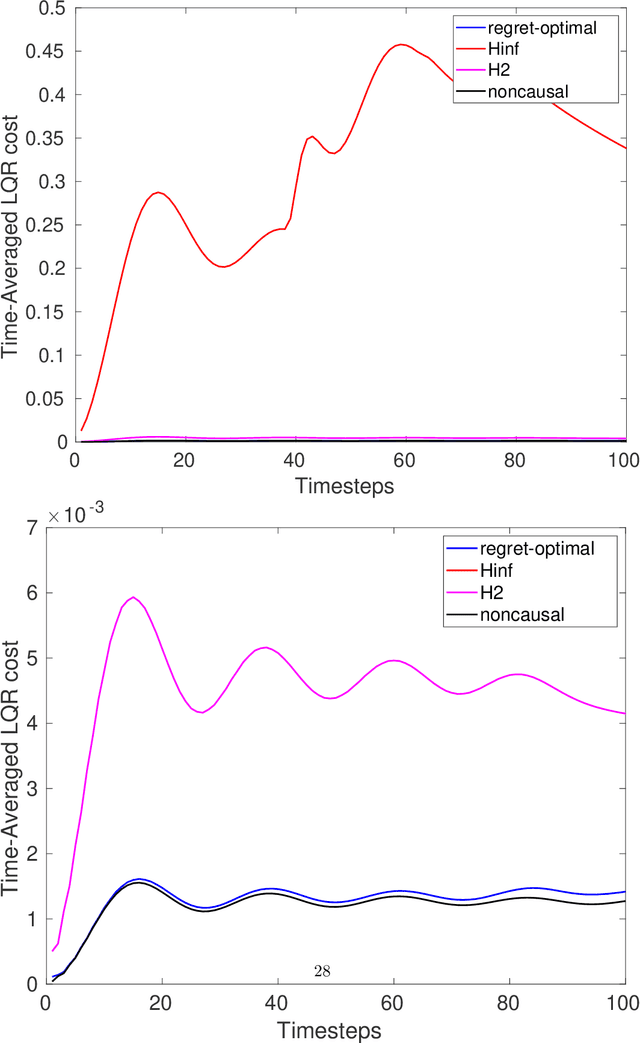
We consider estimation and control in linear time-varying dynamical systems from the perspective of regret minimization. Unlike most prior work in this area, we focus on the problem of designing causal estimators and controllers which compete against a clairvoyant noncausal policy, instead of the best policy selected in hindsight from some fixed parametric class. We show that the regret-optimal estimator and regret-optimal controller can be derived in state-space form using operator-theoretic techniques from robust control and present tight,data-dependent bounds on the regret incurred by our algorithms in terms of the energy of the disturbances. Our results can be viewed as extending traditional robust estimation and control, which focuses on minimizing worst-case cost, to minimizing worst-case regret. We propose regret-optimal analogs of Model-Predictive Control (MPC) and the Extended KalmanFilter (EKF) for systems with nonlinear dynamics and present numerical experiments which show that our regret-optimal algorithms can significantly outperform standard approaches to estimation and control.

Regret-Optimal Full-Information Control

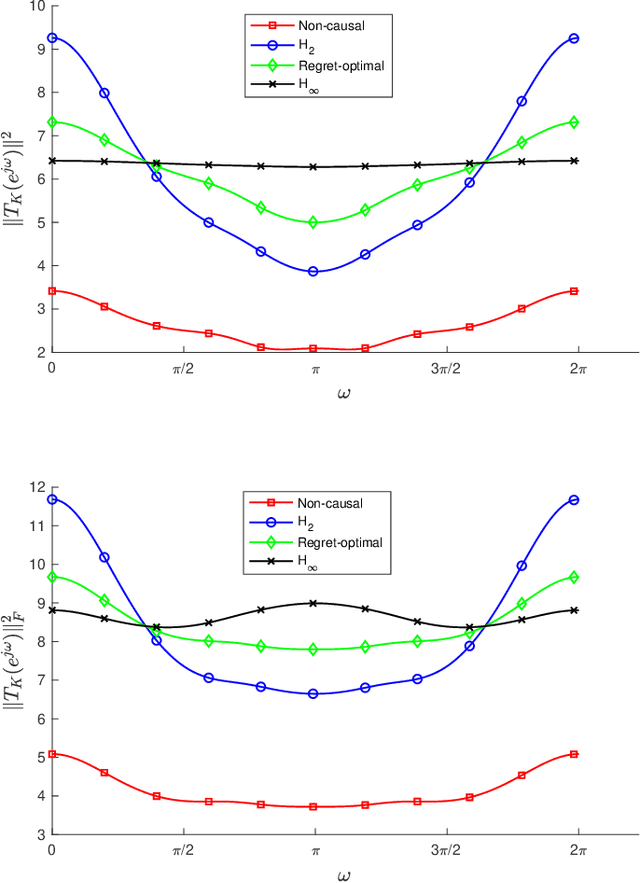
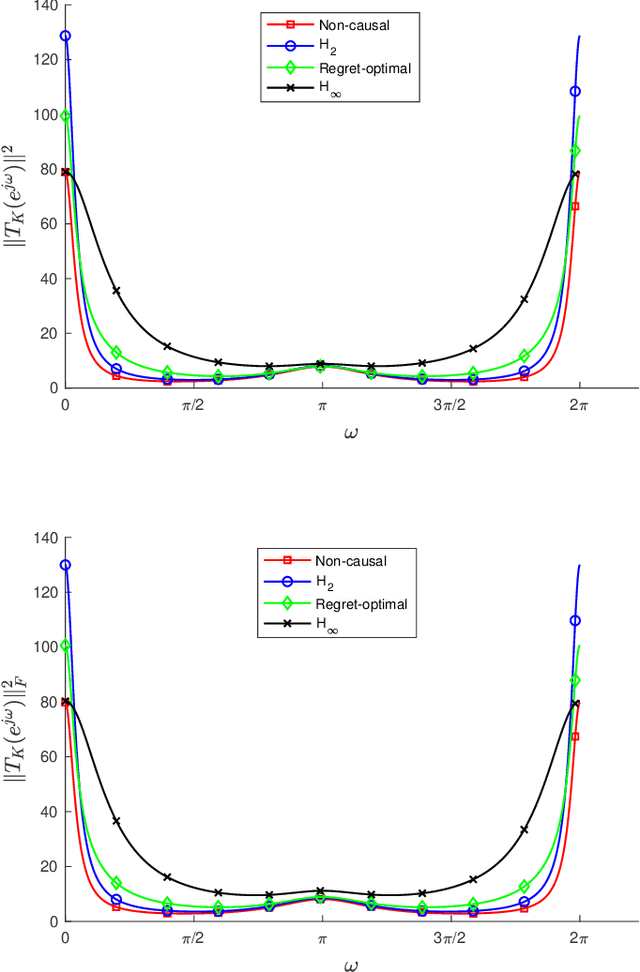
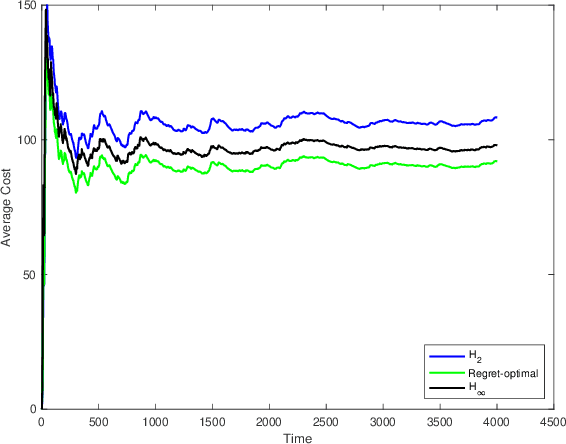
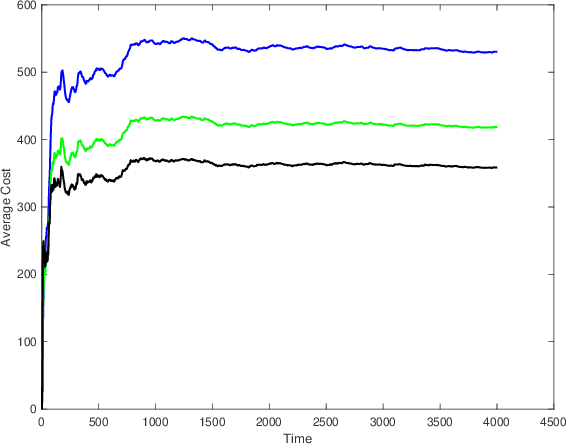
We consider the infinite-horizon, discrete-time full-information control problem. Motivated by learning theory, as a criterion for controller design we focus on regret, defined as the difference between the LQR cost of a causal controller (that has only access to past and current disturbances) and the LQR cost of a clairvoyant one (that has also access to future disturbances). In the full-information setting, there is a unique optimal non-causal controller that in terms of LQR cost dominates all other controllers. Since the regret itself is a function of the disturbances, we consider the worst-case regret over all possible bounded energy disturbances, and propose to find a causal controller that minimizes this worst-case regret. The resulting controller has the interpretation of guaranteeing the smallest possible regret compared to the best non-causal controller, no matter what the future disturbances are. We show that the regret-optimal control problem can be reduced to a Nehari problem, i.e., to approximate an anticausal operator with a causal one in the operator norm. In the state-space setting, explicit formulas for the optimal regret and for the regret-optimal controller (in both the causal and the strictly causal settings) are derived. The regret-optimal controller is the sum of the classical $H_2$ state-feedback law and a finite-dimensional controller obtained from the Nehari problem. The controller construction simply requires the solution to the standard LQR Riccati equation, in addition to two Lyapunov equations. Simulations over a range of plants demonstrates that the regret-optimal controller interpolates nicely between the $H_2$ and the $H_\infty$ optimal controllers, and generally has $H_2$ and $H_\infty$ costs that are simultaneously close to their optimal values. The regret-optimal controller thus presents itself as a viable option for control system design.

Regret-optimal measurement-feedback control

We consider measurement-feedback control in linear dynamical systems from the perspective of regret minimization. Unlike most prior work in this area, we focus on the problem of designing an online controller which competes with the optimal dynamic sequence of control actions selected in hindsight, instead of the best controller in some specific class of controllers. This formulation of regret is attractive when the environment changes over time and no single controller achieves good performance over the entire time horizon. We show that in the measurement-feedback setting, unlike in the full-information setting, there is no single offline controller which outperforms every other offline controller on every disturbance, and propose a new $H_2$-optimal offline controller as a benchmark for the online controller to compete against. We show that the corresponding regret-optimal online controller can be found via a novel reduction to the classical Nehari problem from robust control and present a tight data-dependent bound on its regret.

Regret-optimal control in dynamic environments

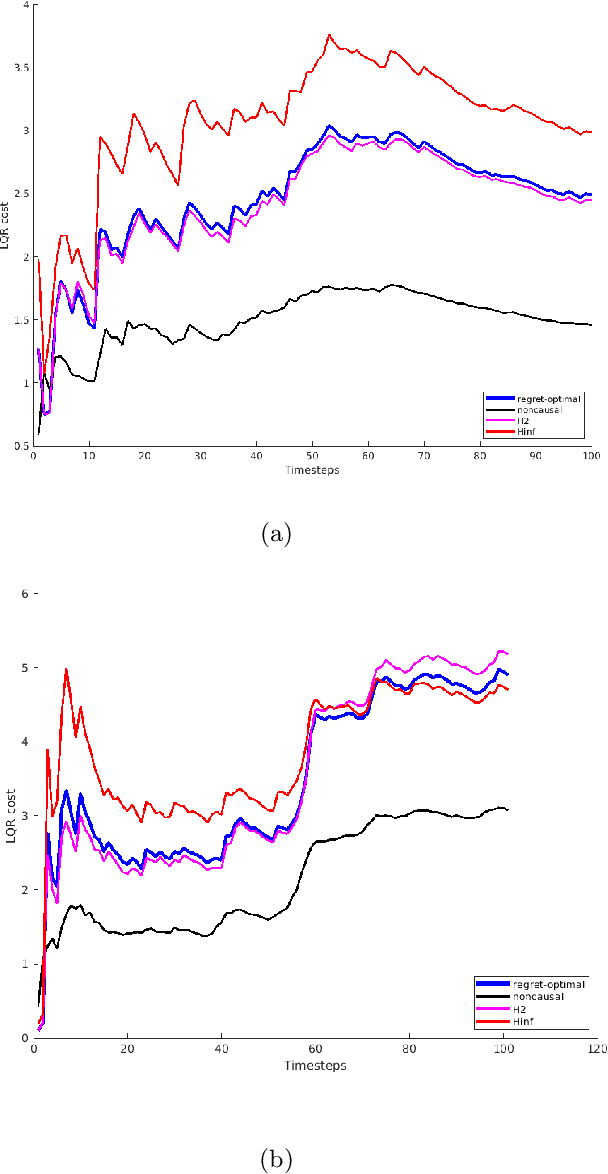
We consider the control of linear time-varying dynamical systems from the perspective of regret minimization. Unlike most prior work in this area, we focus on the problem of designing an online controller which competes with the best dynamic sequence of control actions selected in hindsight, instead of the best controller in some specific class of controllers. This formulation is attractive when the environment changes over time and no single controller achieves good performance over the entire time horizon. We derive the structure of the regret-optimal online controller via a novel reduction to $H_{\infty}$ control and present a clean data-dependent bound on its regret. We also present numerical simulations which confirm that our regret-optimal controller significantly outperforms the $H_2$ and $H_{\infty}$ controllers in dynamic environments.

The Power of Linear Controllers in LQR Control

The Linear Quadratic Regulator (LQR) framework considers the problem of regulating a linear dynamical system perturbed by environmental noise. We compute the policy regret between three distinct control policies: i) the optimal online policy, whose linear structure is given by the Ricatti equations; ii) the optimal offline linear policy, which is the best linear state feedback policy given the noise sequence; and iii) the optimal offline policy, which selects the globally optimal control actions given the noise sequence. We fully characterize the optimal offline policy and show that it has a recursive form in terms of the optimal online policy and future disturbances. We also show that cost of the optimal offline linear policy converges to the cost of the optimal online policy as the time horizon grows large, and consequently the optimal offline linear policy incurs linear regret relative to the optimal offline policy, even in the optimistic setting where the noise is drawn i.i.d from a known distribution. Although we focus on the setting where the noise is stochastic, our results also imply new lower bounds on the policy regret achievable when the noise is chosen by an adaptive adversary.

Online Optimization with Predictions and Non-convex Losses

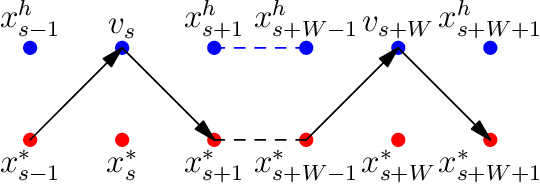
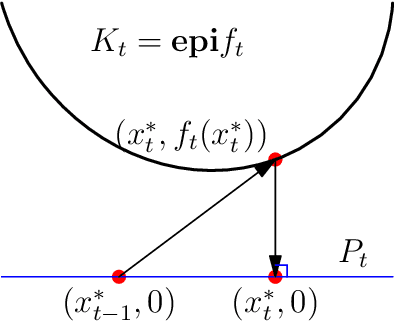
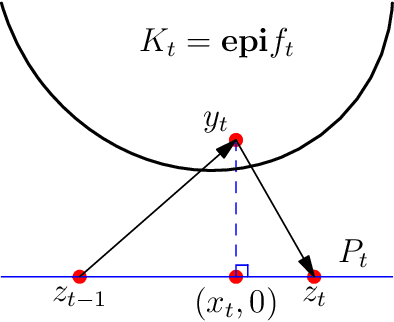
We study online optimization in a setting where an online learner seeks to optimize a per-round hitting cost, which may be non-convex, while incurring a movement cost when changing actions between rounds. We ask: \textit{under what general conditions is it possible for an online learner to leverage predictions of future cost functions in order to achieve near-optimal costs?} Prior work has provided near-optimal online algorithms for specific combinations of assumptions about hitting and switching costs, but no general results are known. In this work, we give two general sufficient conditions that specify a relationship between the hitting and movement costs which guarantees that a new algorithm, Synchronized Fixed Horizon Control (SFHC), provides a $1+O(1/w)$ competitive ratio, where $w$ is the number of predictions available to the learner. Our conditions do not require the cost functions to be convex, and we also derive competitive ratio results for non-convex hitting and movement costs. Our results provide the first constant, dimension-free competitive ratio for online non-convex optimization with movement costs. Further, we give an example of a natural instance, Convex Body Chasing (CBC), where the sufficient conditions are not satisfied and we can prove that no online algorithm can have a competitive ratio that converges to 1.