Sample-Optimal Agnostic Boosting with Unlabeled Data

Boosting provides a practical and provably effective framework for constructing accurate learning algorithms from inaccurate rules of thumb. It extends the promise of sample-efficient learning to settings where direct Empirical Risk Minimization (ERM) may not be implementable efficiently. In the realizable setting, boosting is known to offer this computational reprieve without compromising on sample efficiency. However, in the agnostic case, existing boosting algorithms fall short of achieving the optimal sample complexity. This paper highlights an unexpected and previously unexplored avenue of improvement: unlabeled samples. We design a computationally efficient agnostic boosting algorithm that matches the sample complexity of ERM, given polynomially many additional unlabeled samples. In fact, we show that the total number of samples needed, unlabeled and labeled inclusive, is never more than that for the best known agnostic boosting algorithm -- so this result is never worse -- while only a vanishing fraction of these need to be labeled for the algorithm to succeed. This is particularly fortuitous for learning-theoretic applications of agnostic boosting, which often take place in the distribution-specific setting, where unlabeled samples can be availed for free. We detail other applications of this result in reinforcement learning.

Mind the Gap: Examining the Self-Improvement Capabilities of Large Language Models

Self-improvement is a mechanism in Large Language Model (LLM) pre-training, post-training and test-time inference. We explore a framework where the model verifies its own outputs, filters or reweights data based on this verification, and distills the filtered data. Despite several empirical successes, a fundamental understanding is still lacking. In this work, we initiate a comprehensive, modular and controlled study on LLM self-improvement. We provide a mathematical formulation for self-improvement, which is largely governed by a quantity which we formalize as the generation-verification gap. Through experiments with various model families and tasks, we discover a scaling phenomenon of self-improvement -- a variant of the generation-verification gap scales monotonically with the model pre-training flops. We also examine when self-improvement is possible, an iterative self-improvement procedure, and ways to improve its performance. Our findings not only advance understanding of LLM self-improvement with practical implications, but also open numerous avenues for future research into its capabilities and boundaries.

Sample-Efficient Agnostic Boosting

The theory of boosting provides a computational framework for aggregating approximate weak learning algorithms, which perform marginally better than a random predictor, into an accurate strong learner. In the realizable case, the success of the boosting approach is underscored by a remarkable fact that the resultant sample complexity matches that of a computationally demanding alternative, namely Empirical Risk Minimization (ERM). This in particular implies that the realizable boosting methodology has the potential to offer computational relief without compromising on sample efficiency. Despite recent progress, in agnostic boosting, where assumptions on the conditional distribution of labels given feature descriptions are absent, ERM outstrips the agnostic boosting methodology in being quadratically more sample efficient than all known agnostic boosting algorithms. In this paper, we make progress on closing this gap, and give a substantially more sample efficient agnostic boosting algorithm than those known, without compromising on the computational (or oracle) complexity. A key feature of our algorithm is that it leverages the ability to reuse samples across multiple rounds of boosting, while guaranteeing a generalization error strictly better than those obtained by blackbox applications of uniform convergence arguments. We also apply our approach to other previously studied learning problems, including boosting for reinforcement learning, and demonstrate improved results.

How Does Critical Batch Size Scale in Pre-training?

Training large-scale models under given resources requires careful design of parallelism strategies. In particular, the efficiency notion of critical batch size, concerning the compromise between time and compute, marks the threshold beyond which greater data parallelism leads to diminishing returns. To operationalize it, we propose a measure of CBS and pre-train a series of auto-regressive language models, ranging from 85 million to 1.2 billion parameters, on the C4 dataset. Through extensive hyper-parameter sweeps and careful control on factors such as batch size, momentum, and learning rate along with its scheduling, we systematically investigate the impact of scale on CBS. Then we fit scaling laws with respect to model and data sizes to decouple their effects. Overall, our results demonstrate that CBS scales primarily with data size rather than model size, a finding we justify theoretically through the analysis of infinite-width limits of neural networks and infinite-dimensional least squares regression. Of independent interest, we highlight the importance of common hyper-parameter choices and strategies for studying large-scale pre-training beyond fixed training durations.

Online Nonstochastic Model-Free Reinforcement Learning

In this work, we explore robust model-free reinforcement learning algorithms for environments that may be dynamic or even adversarial. Conventional state-based policies fail to accommodate the challenge imposed by the presence of unmodeled disturbances in such settings. Additionally, optimizing linear state-based policies pose obstacle for efficient optimization, leading to nonconvex objectives even in benign environments like linear dynamical systems. Drawing inspiration from recent advancements in model-based control, we introduce a novel class of policies centered on disturbance signals. We define several categories of these signals, referred to as pseudo-disturbances, and corresponding policy classes based on them. We provide efficient and practical algorithms for optimizing these policies. Next, we examine the task of online adaptation of reinforcement learning agents to adversarial disturbances. Our methods can be integrated with any black-box model-free approach, resulting in provable regret guarantees if the underlying dynamics is linear. We evaluate our method over different standard RL benchmarks and demonstrate improved robustness.

Non-convex online learning via algorithmic equivalence

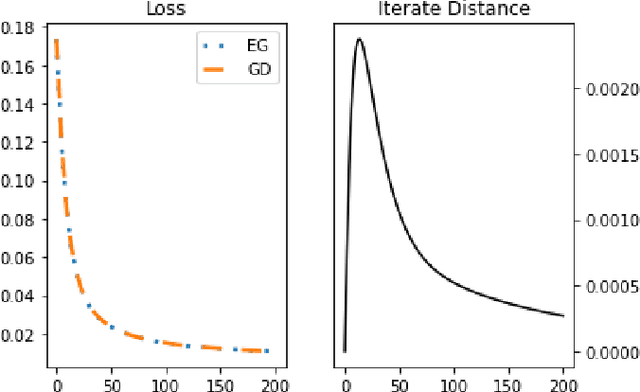
We study an algorithmic equivalence technique between nonconvex gradient descent and convex mirror descent. We start by looking at a harder problem of regret minimization in online non-convex optimization. We show that under certain geometric and smoothness conditions, online gradient descent applied to non-convex functions is an approximation of online mirror descent applied to convex functions under reparameterization. In continuous time, the gradient flow with this reparameterization was shown to be exactly equivalent to continuous-time mirror descent by Amid and Warmuth 2020, but theory for the analogous discrete time algorithms is left as an open problem. We prove an $O(T^{\frac{2}{3}})$ regret bound for non-convex online gradient descent in this setting, answering this open problem. Our analysis is based on a new and simple algorithmic equivalence method.

A Regret Minimization Approach to Multi-Agent Control

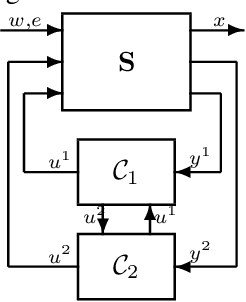
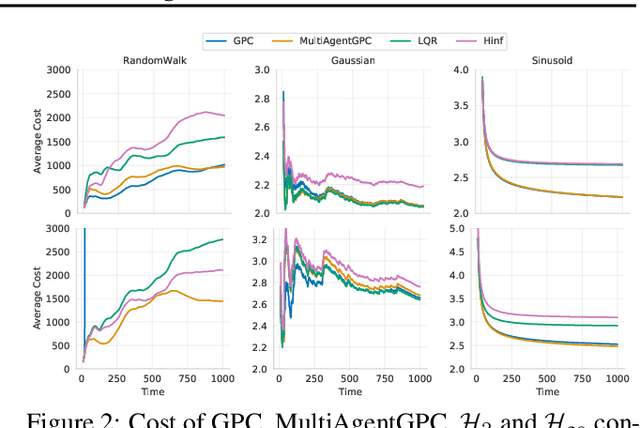
We study the problem of multi-agent control of a dynamical system with known dynamics and adversarial disturbances. Our study focuses on optimal control without centralized precomputed policies, but rather with adaptive control policies for the different agents that are only equipped with a stabilizing controller. We give a reduction from any (standard) regret minimizing control method to a distributed algorithm. The reduction guarantees that the resulting distributed algorithm has low regret relative to the optimal precomputed joint policy. Our methodology involves generalizing online convex optimization to a multi-agent setting and applying recent tools from nonstochastic control derived for a single agent. We empirically evaluate our method on a model of an overactuated aircraft. We show that the distributed method is robust to failure and to adversarial perturbations in the dynamics.

Machine Learning for Mechanical Ventilation Control (Extended Abstract)

Mechanical ventilation is one of the most widely used therapies in the ICU. However, despite broad application from anaesthesia to COVID-related life support, many injurious challenges remain. We frame these as a control problem: ventilators must let air in and out of the patient's lungs according to a prescribed trajectory of airway pressure. Industry-standard controllers, based on the PID method, are neither optimal nor robust. Our data-driven approach learns to control an invasive ventilator by training on a simulator itself trained on data collected from the ventilator. This method outperforms popular reinforcement learning algorithms and even controls the physical ventilator more accurately and robustly than PID. These results underscore how effective data-driven methodologies can be for invasive ventilation and suggest that more general forms of ventilation (e.g., non-invasive, adaptive) may also be amenable.

Robust Online Control with Model Misspecification

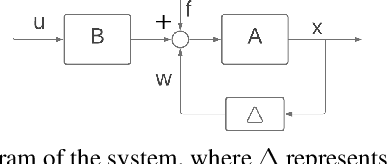
We study online control of an unknown nonlinear dynamical system that is approximated by a time-invariant linear system with model misspecification. Our study focuses on robustness, which measures how much deviation from the assumed linear approximation can be tolerated while maintaining a bounded $\ell_2$-gain compared to the optimal control in hindsight. Some models cannot be stabilized even with perfect knowledge of their coefficients: the robustness is limited by the minimal distance between the assumed dynamics and the set of unstabilizable dynamics. Therefore it is necessary to assume a lower bound on this distance. Under this assumption, and with full observation of the $d$ dimensional state, we describe an efficient controller that attains $\Omega(\frac{1}{\sqrt{d}})$ robustness together with an $\ell_2$-gain whose dimension dependence is near optimal. We also give an inefficient algorithm that attains constant robustness independent of the dimension, with a finite but sub-optimal $\ell_2$-gain.

Machine Learning for Mechanical Ventilation Control

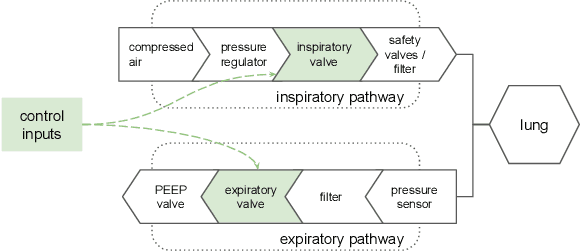
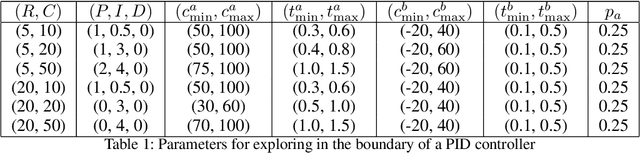
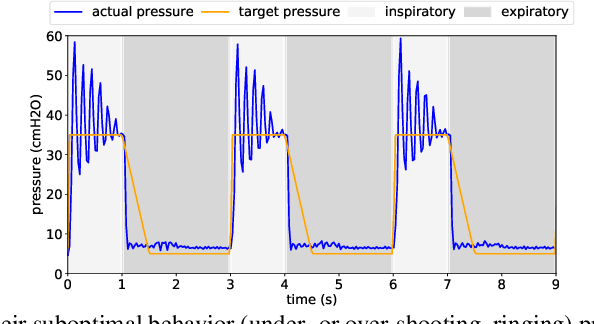
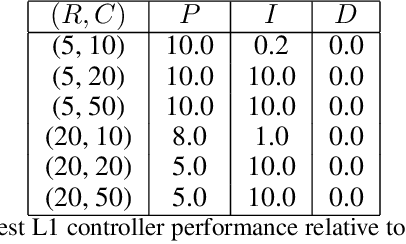
We consider the problem of controlling an invasive mechanical ventilator for pressure-controlled ventilation: a controller must let air in and out of a sedated patient's lungs according to a trajectory of airway pressures specified by a clinician. Hand-tuned PID controllers and similar variants have comprised the industry standard for decades, yet can behave poorly by over- or under-shooting their target or oscillating rapidly. We consider a data-driven machine learning approach: First, we train a simulator based on data we collect from an artificial lung. Then, we train deep neural network controllers on these simulators.We show that our controllers are able to track target pressure waveforms significantly better than PID controllers. We further show that a learned controller generalizes across lungs with varying characteristics much more readily than PID controllers do.