Naixu Guo
AgentIF-OneDay: A Task-level Instruction-Following Benchmark for General AI Agents in Daily Scenarios
Jan 28, 2026Abstract:The capacity of AI agents to effectively handle tasks of increasing duration and complexity continues to grow, demonstrating exceptional performance in coding, deep research, and complex problem-solving evaluations. However, in daily scenarios, the perception of these advanced AI capabilities among general users remains limited. We argue that current evaluations prioritize increasing task difficulty without sufficiently addressing the diversity of agentic tasks necessary to cover the daily work, life, and learning activities of a broad demographic. To address this, we propose AgentIF-OneDay, aimed at determining whether general users can utilize natural language instructions and AI agents to complete a diverse array of daily tasks. These tasks require not only solving problems through dialogue but also understanding various attachment types and delivering tangible file-based results. The benchmark is structured around three user-centric categories: Open Workflow Execution, which assesses adherence to explicit and complex workflows; Latent Instruction, which requires agents to infer implicit instructions from attachments; and Iterative Refinement, which involves modifying or expanding upon ongoing work. We employ instance-level rubrics and a refined evaluation pipeline that aligns LLM-based verification with human judgment, achieving an 80.1% agreement rate using Gemini-3-Pro. AgentIF-OneDay comprises 104 tasks covering 767 scoring points. We benchmarked four leading general AI agents and found that agent products built based on APIs and ChatGPT agents based on agent RL remain in the first tier simultaneously. Leading LLM APIs and open-source models have internalized agentic capabilities, enabling AI application teams to develop cutting-edge Agent products.
Accelerating Inference for Multilayer Neural Networks with Quantum Computers
Oct 08, 2025



Abstract:Fault-tolerant Quantum Processing Units (QPUs) promise to deliver exponential speed-ups in select computational tasks, yet their integration into modern deep learning pipelines remains unclear. In this work, we take a step towards bridging this gap by presenting the first fully-coherent quantum implementation of a multilayer neural network with non-linear activation functions. Our constructions mirror widely used deep learning architectures based on ResNet, and consist of residual blocks with multi-filter 2D convolutions, sigmoid activations, skip-connections, and layer normalizations. We analyse the complexity of inference for networks under three quantum data access regimes. Without any assumptions, we establish a quadratic speedup over classical methods for shallow bilinear-style networks. With efficient quantum access to the weights, we obtain a quartic speedup over classical methods. With efficient quantum access to both the inputs and the network weights, we prove that a network with an $N$-dimensional vectorized input, $k$ residual block layers, and a final residual-linear-pooling layer can be implemented with an error of $\epsilon$ with $O(\text{polylog}(N/\epsilon)^k)$ inference cost.
DeepMath-Creative: A Benchmark for Evaluating Mathematical Creativity of Large Language Models
May 13, 2025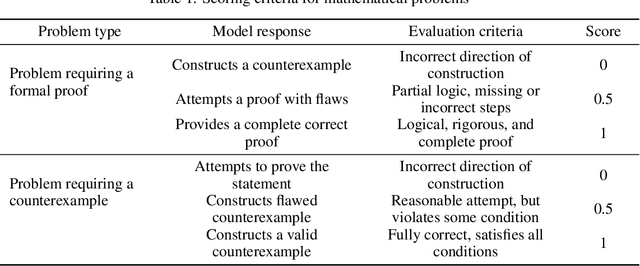
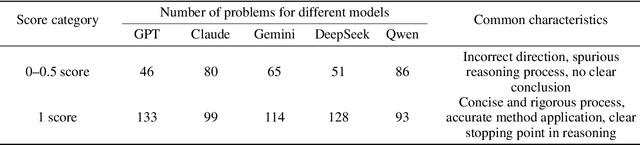
Abstract:To advance the mathematical proficiency of large language models (LLMs), the DeepMath team has launched an open-source initiative aimed at developing an open mathematical LLM and systematically evaluating its mathematical creativity. This paper represents the initial contribution of this initiative. While recent developments in mathematical LLMs have predominantly emphasized reasoning skills, as evidenced by benchmarks on elementary to undergraduate-level mathematical tasks, the creative capabilities of these models have received comparatively little attention, and evaluation datasets remain scarce. To address this gap, we propose an evaluation criteria for mathematical creativity and introduce DeepMath-Creative, a novel, high-quality benchmark comprising constructive problems across algebra, geometry, analysis, and other domains. We conduct a systematic evaluation of mainstream LLMs' creative problem-solving abilities using this dataset. Experimental results show that even under lenient scoring criteria -- emphasizing core solution components and disregarding minor inaccuracies, such as small logical gaps, incomplete justifications, or redundant explanations -- the best-performing model, O3 Mini, achieves merely 70% accuracy, primarily on basic undergraduate-level constructive tasks. Performance declines sharply on more complex problems, with models failing to provide substantive strategies for open problems. These findings suggest that, although current LLMs display a degree of constructive proficiency on familiar and lower-difficulty problems, such performance is likely attributable to the recombination of memorized patterns rather than authentic creative insight or novel synthesis.
Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers
Feb 03, 2025Abstract:This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.
Online Learning of Pure States is as Hard as Mixed States
Feb 02, 2025



Abstract:Quantum state tomography, the task of learning an unknown quantum state, is a fundamental problem in quantum information. In standard settings, the complexity of this problem depends significantly on the type of quantum state that one is trying to learn, with pure states being substantially easier to learn than general mixed states. A natural question is whether this separation holds for any quantum state learning setting. In this work, we consider the online learning framework and prove the surprising result that learning pure states in this setting is as hard as learning mixed states. More specifically, we show that both classes share almost the same sequential fat-shattering dimension, leading to identical regret scaling under the $L_1$-loss. We also generalize previous results on full quantum state tomography in the online setting to learning only partially the density matrix, using smooth analysis.
Quantum linear algebra is all you need for Transformer architectures
Feb 26, 2024



Abstract:Generative machine learning methods such as large-language models are revolutionizing the creation of text and images. While these models are powerful they also harness a large amount of computational resources. The transformer is a key component in large language models that aims to generate a suitable completion of a given partial sequence. In this work, we investigate transformer architectures under the lens of fault-tolerant quantum computing. The input model is one where pre-trained weight matrices are given as block encodings to construct the query, key, and value matrices for the transformer. As a first step, we show how to prepare a block encoding of the self-attention matrix, with a row-wise application of the softmax function using the Hadamard product. In addition, we combine quantum subroutines to construct important building blocks in the transformer, the residual connection, layer normalization, and the feed-forward neural network. Our subroutines prepare an amplitude encoding of the transformer output, which can be measured to obtain a prediction. We discuss the potential and challenges for obtaining a quantum advantage.
Provable learning of quantum states with graphical models
Sep 17, 2023Abstract:The complete learning of an $n$-qubit quantum state requires samples exponentially in $n$. Several works consider subclasses of quantum states that can be learned in polynomial sample complexity such as stabilizer states or high-temperature Gibbs states. Other works consider a weaker sense of learning, such as PAC learning and shadow tomography. In this work, we consider learning states that are close to neural network quantum states, which can efficiently be represented by a graphical model called restricted Boltzmann machines (RBMs). To this end, we exhibit robustness results for efficient provable two-hop neighborhood learning algorithms for ferromagnetic and locally consistent RBMs. We consider the $L_p$-norm as a measure of closeness, including both total variation distance and max-norm distance in the limit. Our results allow certain quantum states to be learned with a sample complexity \textit{exponentially} better than naive tomography. We hence provide new classes of efficiently learnable quantum states and apply new strategies to learn them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge