Learning Theory of Decentralized Robust Kernel-Based Learning Algorithm

We propose a new decentralized robust kernel-based learning algorithm within the framework of reproducing kernel Hilbert space (RKHS) by utilizing a networked system that can be represented as a connected graph. The robust loss function $\mathcal{L}_\sigma$ induced by a windowing function $W$ and a robustness scaling parameter $\sigma>0$, can encompass a broad spectrum of robust losses. Consequently, the proposed algorithm effectively provides a unified decentralized learning framework for robust regression, which fundamentally differs from the existing distributed robust kernel learning schemes, all of which are divide-and-conquer based. We rigorously establish the learning theory and offer a comprehensive convergence analysis for the algorithm. We show each local robust estimator generated from the decentralized algorithm can be utilized to approximate the regression function. Based on kernel-based integral operator techniques, we derive general high confidence convergence bounds for each local approximating sequence in terms of the mean square distance, RKHS norm, and generalization error, respectively. Moreover, we provide rigorous selection rules for local sample size and show that, under properly selected step size and scaling parameter $\sigma$, the decentralized robust algorithm can achieve optimal learning rates (up to logarithmic factors) in both norms. The parameter $\sigma$ is shown to be essential for enhancing robustness while also ensuring favorable convergence behavior. The intrinsic connection among decentralization, sample selection, robustness of the algorithm, and its convergence is clearly reflected.

Hunyuan-TurboS: Advancing Large Language Models through Mamba-Transformer Synergy and Adaptive Chain-of-Thought

As Large Language Models (LLMs) rapidly advance, we introduce Hunyuan-TurboS, a novel large hybrid Transformer-Mamba Mixture of Experts (MoE) model. It synergistically combines Mamba's long-sequence processing efficiency with Transformer's superior contextual understanding. Hunyuan-TurboS features an adaptive long-short chain-of-thought (CoT) mechanism, dynamically switching between rapid responses for simple queries and deep "thinking" modes for complex problems, optimizing computational resources. Architecturally, this 56B activated (560B total) parameter model employs 128 layers (Mamba2, Attention, FFN) with an innovative AMF/MF block pattern. Faster Mamba2 ensures linear complexity, Grouped-Query Attention minimizes KV cache, and FFNs use an MoE structure. Pre-trained on 16T high-quality tokens, it supports a 256K context length and is the first industry-deployed large-scale Mamba model. Our comprehensive post-training strategy enhances capabilities via Supervised Fine-Tuning (3M instructions), a novel Adaptive Long-short CoT Fusion method, Multi-round Deliberation Learning for iterative improvement, and a two-stage Large-scale Reinforcement Learning process targeting STEM and general instruction-following. Evaluations show strong performance: overall top 7 rank on LMSYS Chatbot Arena with a score of 1356, outperforming leading models like Gemini-2.0-Flash-001 (1352) and o4-mini-2025-04-16 (1345). TurboS also achieves an average of 77.9% across 23 automated benchmarks. Hunyuan-TurboS balances high performance and efficiency, offering substantial capabilities at lower inference costs than many reasoning models, establishing a new paradigm for efficient large-scale pre-trained models.

Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers

This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.

Quantum linear algebra is all you need for Transformer architectures

Generative machine learning methods such as large-language models are revolutionizing the creation of text and images. While these models are powerful they also harness a large amount of computational resources. The transformer is a key component in large language models that aims to generate a suitable completion of a given partial sequence. In this work, we investigate transformer architectures under the lens of fault-tolerant quantum computing. The input model is one where pre-trained weight matrices are given as block encodings to construct the query, key, and value matrices for the transformer. As a first step, we show how to prepare a block encoding of the self-attention matrix, with a row-wise application of the softmax function using the Hadamard product. In addition, we combine quantum subroutines to construct important building blocks in the transformer, the residual connection, layer normalization, and the feed-forward neural network. Our subroutines prepare an amplitude encoding of the transformer output, which can be measured to obtain a prediction. We discuss the potential and challenges for obtaining a quantum advantage.

Provable Advantage of Parameterized Quantum Circuit in Function Approximation

Understanding the power of parameterized quantum circuits (PQCs) in accomplishing machine learning tasks is one of the most important questions in quantum machine learning. In this paper, we analyze the expressivity of PQCs through the lens of function approximation. Previously established universal approximation theorems for PQCs are mainly nonconstructive, leading us to the following question: How large do the PQCs need to be to approximate the target function up to a given error? We exhibit explicit constructions of data re-uploading PQCs for approximating continuous and smooth functions and establish quantitative approximation error bounds in terms of the width, the depth and the number of trainable parameters of the PQCs. To achieve this, we utilize techniques from quantum signal processing and linear combinations of unitaries to construct PQCs that implement multivariate polynomials. We implement global and local approximation techniques using Bernstein polynomials and local Taylor expansion and analyze their performances in the quantum setting. We also compare our proposed PQCs to nearly optimal deep neural networks in approximating high-dimensional smooth functions, showing that the ratio between model sizes of PQC and deep neural networks is exponentially small with respect to the input dimension. This suggests a potentially novel avenue for showcasing quantum advantages in quantum machine learning.

Learning Theory of Distribution Regression with Neural Networks

In this paper, we aim at establishing an approximation theory and a learning theory of distribution regression via a fully connected neural network (FNN). In contrast to the classical regression methods, the input variables of distribution regression are probability measures. Then we often need to perform a second-stage sampling process to approximate the actual information of the distribution. On the other hand, the classical neural network structure requires the input variable to be a vector. When the input samples are probability distributions, the traditional deep neural network method cannot be directly used and the difficulty arises for distribution regression. A well-defined neural network structure for distribution inputs is intensively desirable. There is no mathematical model and theoretical analysis on neural network realization of distribution regression. To overcome technical difficulties and address this issue, we establish a novel fully connected neural network framework to realize an approximation theory of functionals defined on the space of Borel probability measures. Furthermore, based on the established functional approximation results, in the hypothesis space induced by the novel FNN structure with distribution inputs, almost optimal learning rates for the proposed distribution regression model up to logarithmic terms are derived via a novel two-stage error decomposition technique.

Distributed Gradient Descent for Functional Learning

In recent years, different types of distributed learning schemes have received increasing attention for their strong advantages in handling large-scale data information. In the information era, to face the big data challenges which stem from functional data analysis very recently, we propose a novel distributed gradient descent functional learning (DGDFL) algorithm to tackle functional data across numerous local machines (processors) in the framework of reproducing kernel Hilbert space. Based on integral operator approaches, we provide the first theoretical understanding of the DGDFL algorithm in many different aspects in the literature. On the way of understanding DGDFL, firstly, a data-based gradient descent functional learning (GDFL) algorithm associated with a single-machine model is proposed and comprehensively studied. Under mild conditions, confidence-based optimal learning rates of DGDFL are obtained without the saturation boundary on the regularity index suffered in previous works in functional regression. We further provide a semi-supervised DGDFL approach to weaken the restriction on the maximal number of local machines to ensure optimal rates. To our best knowledge, the DGDFL provides the first distributed iterative training approach to functional learning and enriches the stage of functional data analysis.

Efficient information recovery from Pauli noise via classical shadow

The rapid advancement of quantum computing has led to an extensive demand for effective techniques to extract classical information from quantum systems, particularly in fields like quantum machine learning and quantum chemistry. However, quantum systems are inherently susceptible to noises, which adversely corrupt the information encoded in quantum systems. In this work, we introduce an efficient algorithm that can recover information from quantum states under Pauli noise. The core idea is to learn the necessary information of the unknown Pauli channel by post-processing the classical shadows of the channel. For a local and bounded-degree observable, only partial knowledge of the channel is required rather than its complete classical description to recover the ideal information, resulting in a polynomial-time algorithm. This contrasts with conventional methods such as probabilistic error cancellation, which requires the full information of the channel and exhibits exponential scaling with the number of qubits. We also prove that this scalable method is optimal on the sample complexity and generalise the algorithm to the weight contracting channel. Furthermore, we demonstrate the validity of the algorithm on the 1D anisotropic Heisenberg-type model via numerical simulations. As a notable application, our method can be severed as a sample-efficient error mitigation scheme for Clifford circuits.

Power and limitations of single-qubit native quantum neural networks

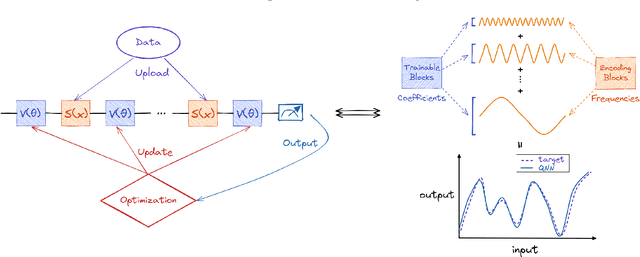
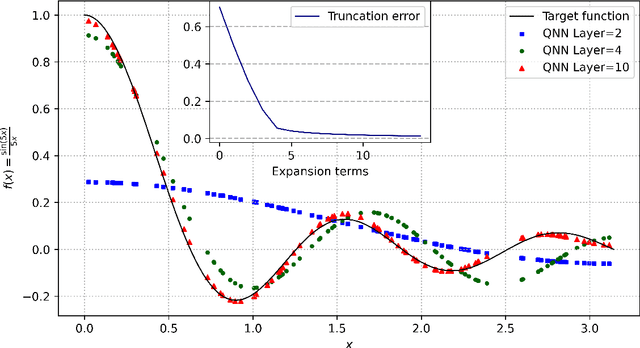
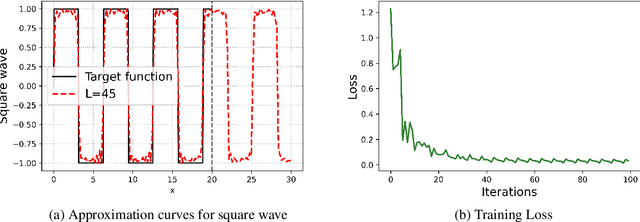
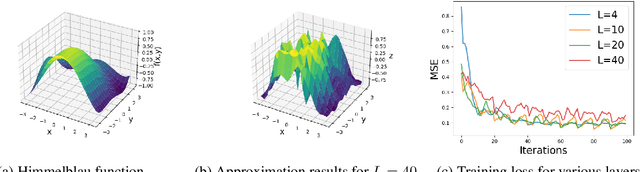
Quantum neural networks (QNNs) have emerged as a leading strategy to establish applications in machine learning, chemistry, and optimization. While the applications of QNN have been widely investigated, its theoretical foundation remains less understood. In this paper, we formulate a theoretical framework for the expressive ability of data re-uploading quantum neural networks that consist of interleaved encoding circuit blocks and trainable circuit blocks. First, we prove that single-qubit quantum neural networks can approximate any univariate function by mapping the model to a partial Fourier series. Beyond previous works' understanding of existence, we in particular establish the exact correlations between the parameters of the trainable gates and the working Fourier coefficients, by exploring connections to quantum signal processing. Second, we discuss the limitations of single-qubit native QNNs on approximating multivariate functions by analyzing the frequency spectrum and the flexibility of Fourier coefficients. We further demonstrate the expressivity and limitations of single-qubit native QNNs via numerical experiments. As applications, we introduce natural extensions to multi-qubit quantum neural networks, which exhibit the capability of classifying real-world multi-dimensional data. We believe these results would improve our understanding of QNNs and provide a helpful guideline for designing powerful QNNs for machine learning tasks.

Optimal quantum dataset for learning a unitary transformation

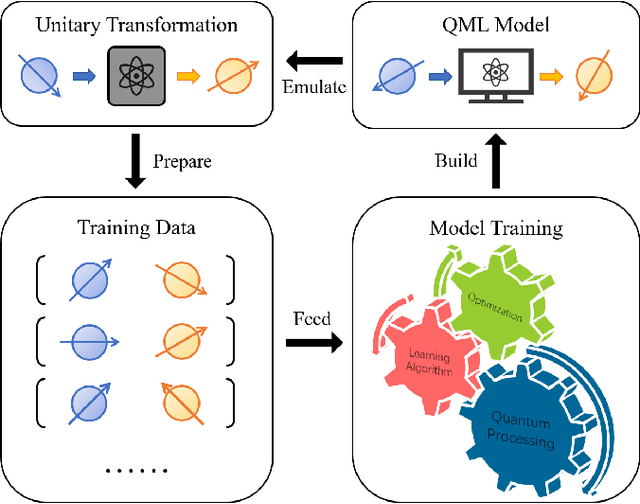
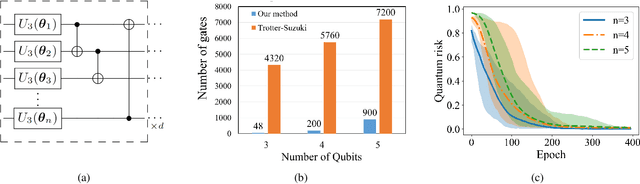
Unitary transformations formulate the time evolution of quantum states. How to learn a unitary transformation efficiently is a fundamental problem in quantum machine learning. The most natural and leading strategy is to train a quantum machine learning model based on a quantum dataset. Although presence of more training data results in better models, using too much data reduces the efficiency of training. In this work, we solve the problem on the minimum size of sufficient quantum datasets for learning a unitary transformation exactly, which reveals the power and limitation of quantum data. First, we prove that the minimum size of dataset with pure states is $2^n$ for learning an $n$-qubit unitary transformation. To fully explore the capability of quantum data, we introduce a quantum dataset consisting of $n+1$ mixed states that are sufficient for exact training. The main idea is to simplify the structure utilizing decoupling, which leads to an exponential improvement on the size over the datasets with pure states. Furthermore, we show that the size of quantum dataset with mixed states can be reduced to a constant, which yields an optimal quantum dataset for learning a unitary. We showcase the applications of our results in oracle compiling and Hamiltonian simulation. Notably, to accurately simulate a 3-qubit one-dimensional nearest-neighbor Heisenberg model, our circuit only uses $48$ elementary quantum gates, which is significantly less than $4320$ gates in the circuit constructed by the Trotter-Suzuki product formula.