Accelerating Inference for Multilayer Neural Networks with Quantum Computers

Fault-tolerant Quantum Processing Units (QPUs) promise to deliver exponential speed-ups in select computational tasks, yet their integration into modern deep learning pipelines remains unclear. In this work, we take a step towards bridging this gap by presenting the first fully-coherent quantum implementation of a multilayer neural network with non-linear activation functions. Our constructions mirror widely used deep learning architectures based on ResNet, and consist of residual blocks with multi-filter 2D convolutions, sigmoid activations, skip-connections, and layer normalizations. We analyse the complexity of inference for networks under three quantum data access regimes. Without any assumptions, we establish a quadratic speedup over classical methods for shallow bilinear-style networks. With efficient quantum access to the weights, we obtain a quartic speedup over classical methods. With efficient quantum access to both the inputs and the network weights, we prove that a network with an $N$-dimensional vectorized input, $k$ residual block layers, and a final residual-linear-pooling layer can be implemented with an error of $\epsilon$ with $O(\text{polylog}(N/\epsilon)^k)$ inference cost.

A Domain-agnostic, Noise-resistant, Hardware-efficient Evolutionary Variational Quantum Eigensolver

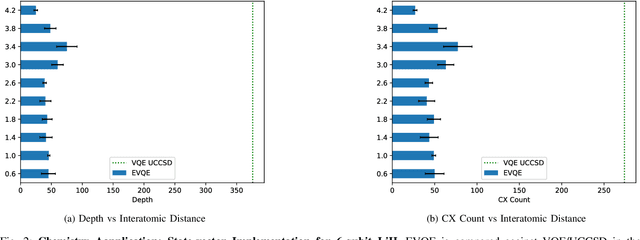
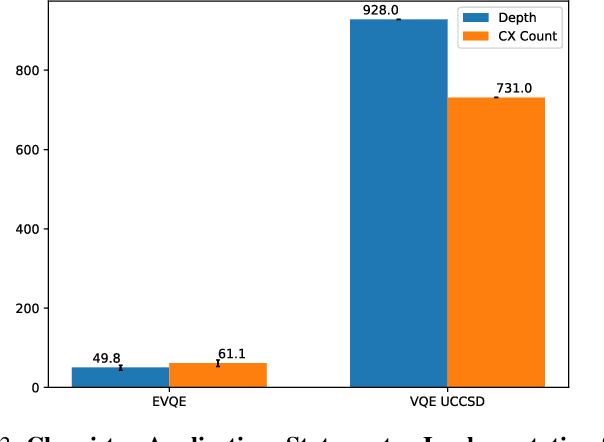
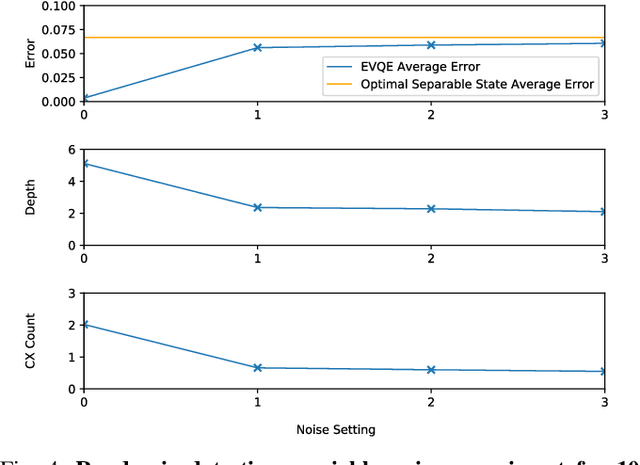
Variational quantum algorithms have shown promise in numerous fields due to their versatility in solving problems of scientific and commercial interest. However, leading algorithms for Hamiltonian simulation, such as the Variational Quantum Eigensolver (VQE), use fixed preconstructed ansatzes, limiting their general applicability and accuracy. Thus, variational forms---the quantum circuits that implement ansatzes ---are either crafted heuristically or by encoding domain-specific knowledge. In this paper, we present an Evolutionary Variational Quantum Eigensolver (EVQE), a novel variational algorithm that uses evolutionary programming techniques to minimize the expectation value of a given Hamiltonian by dynamically generating and optimizing an ansatz. The algorithm is equally applicable to optimization problems in all domains, obtaining accurate energy evaluations with hardware-efficient ansatzes. In molecular simulations, the variational forms generated by EVQE are up to $18.6\times$ shallower and use up to $12\times$ fewer CX gates than those obtained by VQE with a unitary coupled cluster ansatz. EVQE demonstrates significant noise-resistance properties, obtaining results in noisy simulation with at least $3.6\times$ less error than VQE using any tested ansatz configuration. We successfully evaluated EVQE on a real 5-qubit IBMQ quantum computer. The experimental results, which we obtained both via simulation and on real quantum hardware, demonstrate the effectiveness of EVQE for general-purpose optimization on the quantum computers of the present and near future.