Multimodal Autoregressive Pre-training of Large Vision Encoders

We introduce a novel method for pre-training of large-scale vision encoders. Building on recent advancements in autoregressive pre-training of vision models, we extend this framework to a multimodal setting, i.e., images and text. In this paper, we present AIMV2, a family of generalist vision encoders characterized by a straightforward pre-training process, scalability, and remarkable performance across a range of downstream tasks. This is achieved by pairing the vision encoder with a multimodal decoder that autoregressively generates raw image patches and text tokens. Our encoders excel not only in multimodal evaluations but also in vision benchmarks such as localization, grounding, and classification. Notably, our AIMV2-3B encoder achieves 89.5% accuracy on ImageNet-1k with a frozen trunk. Furthermore, AIMV2 consistently outperforms state-of-the-art contrastive models (e.g., CLIP, SigLIP) in multimodal image understanding across diverse settings.

Sparse Repellency for Shielded Generation in Text-to-image Diffusion Models

The increased adoption of diffusion models in text-to-image generation has triggered concerns on their reliability. Such models are now closely scrutinized under the lens of various metrics, notably calibration, fairness, or compute efficiency. We focus in this work on two issues that arise when deploying these models: a lack of diversity when prompting images, and a tendency to recreate images from the training set. To solve both problems, we propose a method that coaxes the sampled trajectories of pretrained diffusion models to land on images that fall outside of a reference set. We achieve this by adding repellency terms to the diffusion SDE throughout the generation trajectory, which are triggered whenever the path is expected to land too closely to an image in the shielded reference set. Our method is sparse in the sense that these repellency terms are zero and inactive most of the time, and even more so towards the end of the generation trajectory. Our method, named SPELL for sparse repellency, can be used either with a static reference set that contains protected images, or dynamically, by updating the set at each timestep with the expected images concurrently generated within a batch. We show that adding SPELL to popular diffusion models improves their diversity while impacting their FID only marginally, and performs comparatively better than other recent training-free diversity methods. We also demonstrate how SPELL can ensure a shielded generation away from a very large set of protected images by considering all 1.2M images from ImageNet as the protected set.

Graph-Based Captioning: Enhancing Visual Descriptions by Interconnecting Region Captions

Humans describe complex scenes with compositionality, using simple text descriptions enriched with links and relationships. While vision-language research has aimed to develop models with compositional understanding capabilities, this is not reflected yet in existing datasets which, for the most part, still use plain text to describe images. In this work, we propose a new annotation strategy, graph-based captioning (GBC) that describes an image using a labelled graph structure, with nodes of various types. The nodes in GBC are created using, in a first stage, object detection and dense captioning tools nested recursively to uncover and describe entity nodes, further linked together in a second stage by highlighting, using new types of nodes, compositions and relations among entities. Since all GBC nodes hold plain text descriptions, GBC retains the flexibility found in natural language, but can also encode hierarchical information in its edges. We demonstrate that GBC can be produced automatically, using off-the-shelf multimodal LLMs and open-vocabulary detection models, by building a new dataset, GBC10M, gathering GBC annotations for about 10M images of the CC12M dataset. We use GBC10M to showcase the wealth of node captions uncovered by GBC, as measured with CLIP training. We show that using GBC nodes' annotations -- notably those stored in composition and relation nodes -- results in significant performance boost on downstream models when compared to other dataset formats. To further explore the opportunities provided by GBC, we also propose a new attention mechanism that can leverage the entire GBC graph, with encouraging experimental results that show the extra benefits of incorporating the graph structure. Our datasets are released at \url{https://huggingface.co/graph-based-captions}.

TaCo: Targeted Concept Removal in Output Embeddings for NLP via Information Theory and Explainability

The fairness of Natural Language Processing (NLP) models has emerged as a crucial concern. Information theory indicates that to achieve fairness, a model should not be able to predict sensitive variables, such as gender, ethnicity, and age. However, information related to these variables often appears implicitly in language, posing a challenge in identifying and mitigating biases effectively. To tackle this issue, we present a novel approach that operates at the embedding level of an NLP model, independent of the specific architecture. Our method leverages insights from recent advances in XAI techniques and employs an embedding transformation to eliminate implicit information from a selected variable. By directly manipulating the embeddings in the final layer, our approach enables a seamless integration into existing models without requiring significant modifications or retraining. In evaluation, we show that the proposed post-hoc approach significantly reduces gender-related associations in NLP models while preserving the overall performance and functionality of the models. An implementation of our method is available: https://github.com/fanny-jourdan/TaCo

Improved learning theory for kernel distribution regression with two-stage sampling

The distribution regression problem encompasses many important statistics and machine learning tasks, and arises in a large range of applications. Among various existing approaches to tackle this problem, kernel methods have become a method of choice. Indeed, kernel distribution regression is both computationally favorable, and supported by a recent learning theory. This theory also tackles the two-stage sampling setting, where only samples from the input distributions are available. In this paper, we improve the learning theory of kernel distribution regression. We address kernels based on Hilbertian embeddings, that encompass most, if not all, of the existing approaches. We introduce the novel near-unbiased condition on the Hilbertian embeddings, that enables us to provide new error bounds on the effect of the two-stage sampling, thanks to a new analysis. We show that this near-unbiased condition holds for three important classes of kernels, based on optimal transport and mean embedding. As a consequence, we strictly improve the existing convergence rates for these kernels. Our setting and results are illustrated by numerical experiments.

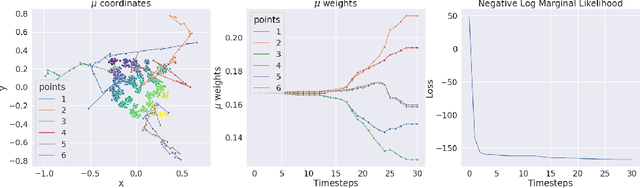
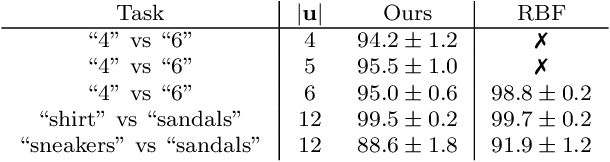
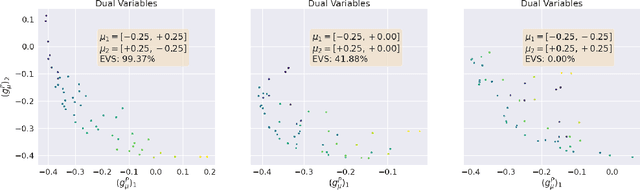
Gaussian Processes on Distributions based on Regularized Optimal Transport

We present a novel kernel over the space of probability measures based on the dual formulation of optimal regularized transport. We propose an Hilbertian embedding of the space of probabilities using their Sinkhorn potentials, which are solutions of the dual entropic relaxed optimal transport between the probabilities and a reference measure $\mathcal{U}$. We prove that this construction enables to obtain a valid kernel, by using the Hilbert norms. We prove that the kernel enjoys theoretical properties such as universality and some invariances, while still being computationally feasible. Moreover we provide theoretical guarantees on the behaviour of a Gaussian process based on this kernel. The empirical performances are compared with other traditional choices of kernels for processes indexed on distributions.

When adversarial attacks become interpretable counterfactual explanations

We argue that, when learning a 1-Lipschitz neural network with the dual loss of an optimal transportation problem, the gradient of the model is both the direction of the transportation plan and the direction to the closest adversarial attack. Traveling along the gradient to the decision boundary is no more an adversarial attack but becomes a counterfactual explanation, explicitly transporting from one class to the other. Through extensive experiments on XAI metrics, we find that the simple saliency map method, applied on such networks, becomes a reliable explanation, and outperforms the state-of-the-art explanation approaches on unconstrained models. The proposed networks were already known to be certifiably robust, and we prove that they are also explainable with a fast and simple method.

GAN Estimation of Lipschitz Optimal Transport Maps

This paper introduces the first statistically consistent estimator of the optimal transport map between two probability distributions, based on neural networks. Building on theoretical and practical advances in the field of Lipschitz neural networks, we define a Lipschitz-constrained generative adversarial network penalized by the quadratic transportation cost. Then, we demonstrate that, under regularity assumptions, the obtained generator converges uniformly to the optimal transport map as the sample size increases to infinity. Furthermore, we show through a number of numerical experiments that the learnt mapping has promising performances. In contrast to previous work tackling either statistical guarantees or practicality, we provide an expressive and feasible estimator which paves way for optimal transport applications where the asymptotic behaviour must be certified.

The Many Faces of 1-Lipschitz Neural Networks

Lipschitz constrained models have been used to solve specifics deep learning problems such as the estimation of Wasserstein distance for GAN, or the training of neural networks robust to adversarial attacks. Regardless the novel and effective algorithms to build such 1-Lipschitz networks, their usage remains marginal, and they are commonly considered as less expressive and less able to fit properly the data than their unconstrained counterpart. The goal of the paper is to demonstrate that, despite being empirically harder to train, 1-Lipschitz neural networks are theoretically better grounded than unconstrained ones when it comes to classification. To achieve that we recall some results about 1-Lipschitz function in the scope of deep learning and we extend and illustrate them to derive general properties for classification. First, we show that 1-Lipschitz neural network can fit arbitrarily difficult frontier making them as expressive as classical ones. When minimizing the log loss, we prove that the optimization problem under Lipschitz constraint is well posed and have a minimum, whereas regular neural networks can diverge even on remarkably simple situations. Then, we study the link between classification with 1-Lipschitz network and optimal transport thanks to regularized versions of Kantorovich-Rubinstein duality theory. Last, we derive preliminary bounds on their VC dimension.

Ranking Deep Learning Generalization using Label Variation in Latent Geometry Graphs

Measuring the generalization performance of a Deep Neural Network (DNN) without relying on a validation set is a difficult task. In this work, we propose exploiting Latent Geometry Graphs (LGGs) to represent the latent spaces of trained DNN architectures. Such graphs are obtained by connecting samples that yield similar latent representations at a given layer of the considered DNN. We then obtain a generalization score by looking at how strongly connected are samples of distinct classes in LGGs. This score allowed us to rank 3rd on the NeurIPS 2020 Predicting Generalization in Deep Learning (PGDL) competition.