Lin F. Yang
Preference-based Reinforcement Learning with Finite-Time Guarantees
Jun 16, 2020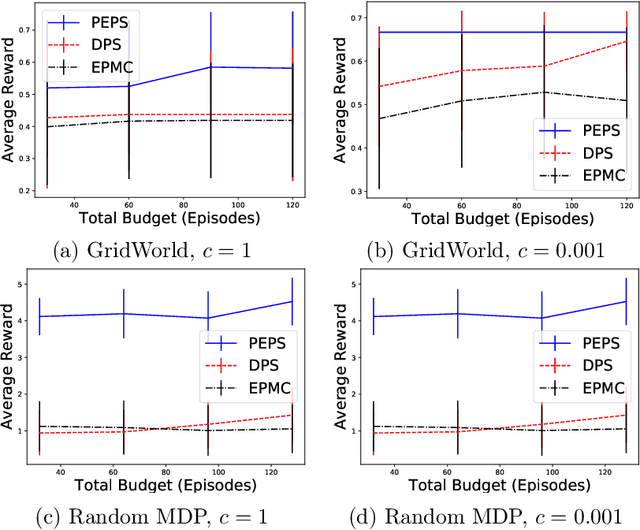
Abstract:Preference-based Reinforcement Learning (PbRL) replaces reward values in traditional reinforcement learning by preferences to better elicit human opinion on the target objective, especially when numerical reward values are hard to design or interpret. Despite promising results in applications, the theoretical understanding of PbRL is still in its infancy. In this paper, we present the first finite-time analysis for general PbRL problems. We first show that a unique optimal policy may not exist if preferences over trajectories are deterministic for PbRL. If preferences are stochastic, and the preference probability relates to the hidden reward values, we present algorithms for PbRL, both with and without a simulator, that are able to identify the best policy up to accuracy $\varepsilon$ with high probability. Our method explores the state space by navigating to under-explored states, and solves PbRL using a combination of dueling bandits and policy search. Experiments show the efficacy of our method when it is applied to real-world problems.
Model-Based Reinforcement Learning with Value-Targeted Regression
Jun 01, 2020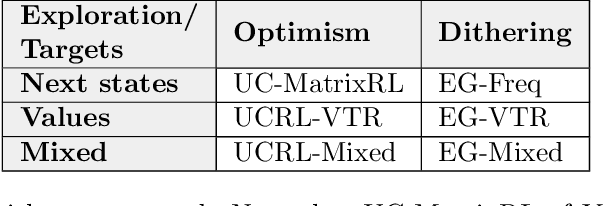
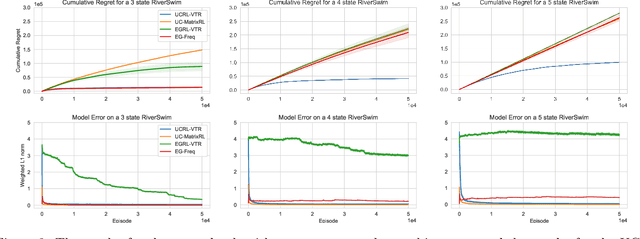
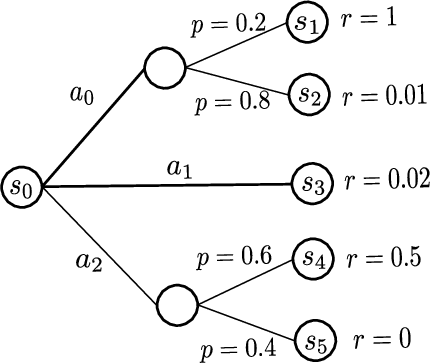
Abstract:This paper studies model-based reinforcement learning (RL) for regret minimization. We focus on finite-horizon episodic RL where the transition model $P$ belongs to a known family of models $\mathcal{P}$, a special case of which is when models in $\mathcal{P}$ take the form of linear mixtures: $P_{\theta} = \sum_{i=1}^{d} \theta_{i}P_{i}$. We propose a model based RL algorithm that is based on optimism principle: In each episode, the set of models that are `consistent' with the data collected is constructed. The criterion of consistency is based on the total squared error of that the model incurs on the task of predicting \emph{values} as determined by the last value estimate along the transitions. The next value function is then chosen by solving the optimistic planning problem with the constructed set of models. We derive a bound on the regret, which, in the special case of linear mixtures, the regret bound takes the form $\tilde{\mathcal{O}}(d\sqrt{H^{3}T})$, where $H$, $T$ and $d$ are the horizon, total number of steps and dimension of $\theta$, respectively. In particular, this regret bound is independent of the total number of states or actions, and is close to a lower bound $\Omega(\sqrt{HdT})$. For a general model family $\mathcal{P}$, the regret bound is derived using the notion of the so-called Eluder dimension proposed by Russo & Van Roy (2014).
Is Long Horizon Reinforcement Learning More Difficult Than Short Horizon Reinforcement Learning?
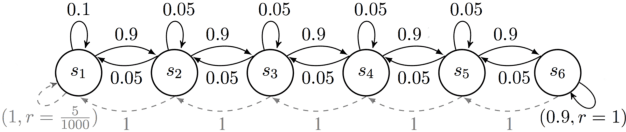
May 01, 2020Abstract:Learning to plan for long horizons is a central challenge in episodic reinforcement learning problems. A fundamental question is to understand how the difficulty of the problem scales as the horizon increases. Here the natural measure of sample complexity is a normalized one: we are interested in the number of episodes it takes to provably discover a policy whose value is $\varepsilon$ near to that of the optimal value, where the value is measured by the normalized cumulative reward in each episode. In a COLT 2018 open problem, Jiang and Agarwal conjectured that, for tabular, episodic reinforcement learning problems, there exists a sample complexity lower bound which exhibits a polynomial dependence on the horizon -- a conjecture which is consistent with all known sample complexity upper bounds. This work refutes this conjecture, proving that tabular, episodic reinforcement learning is possible with a sample complexity that scales only logarithmically with the planning horizon. In other words, when the values are appropriately normalized (to lie in the unit interval), this results shows that long horizon RL is no more difficult than short horizon RL, at least in a minimax sense. Our analysis introduces two ideas: (i) the construction of an $\varepsilon$-net for optimal policies whose log-covering number scales only logarithmically with the planning horizon, and (ii) the Online Trajectory Synthesis algorithm, which adaptively evaluates all policies in a given policy class using sample complexity that scales with the log-covering number of the given policy class. Both may be of independent interest.
Provably Efficient Exploration for RL with Unsupervised Learning
Mar 15, 2020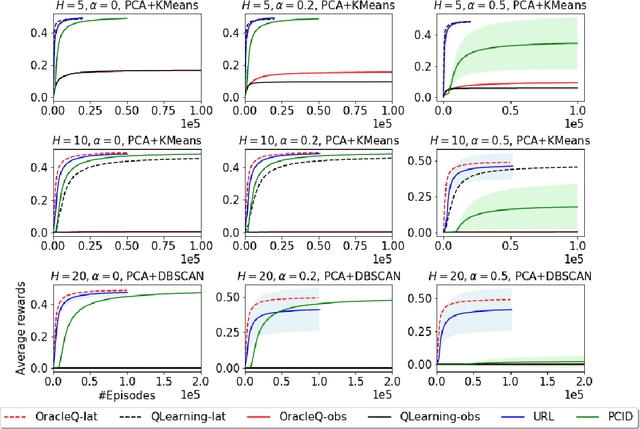
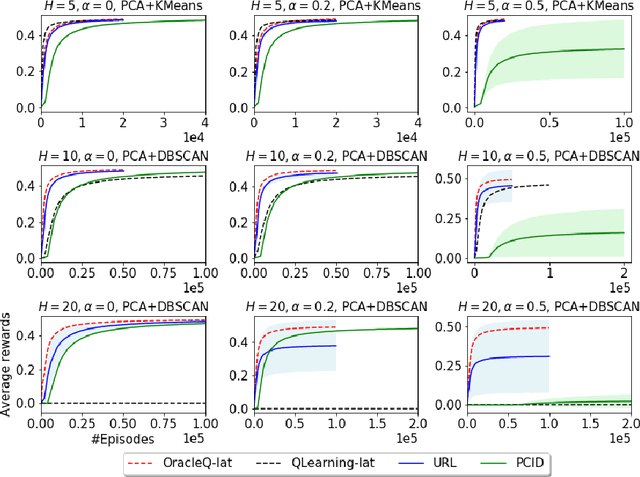
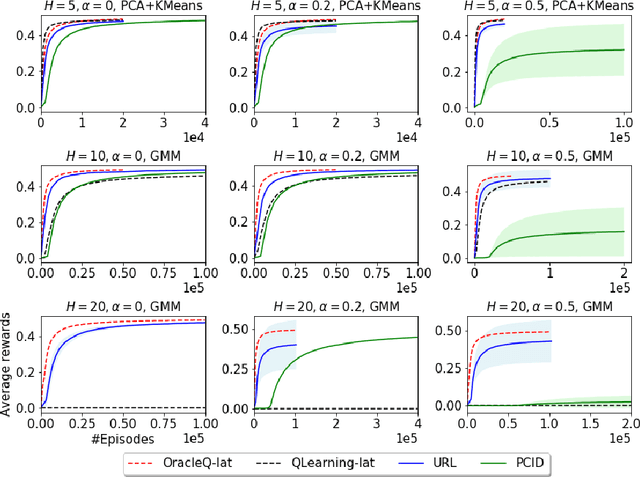
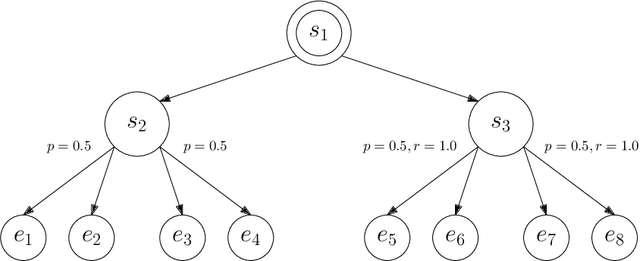
Abstract:We study how to use unsupervised learning for efficient exploration in reinforcement learning with rich observations generated from a small number of latent states. We present a novel algorithmic framework that is built upon two components: an unsupervised learning algorithm and a no-regret reinforcement learning algorithm. We show that our algorithm provably finds a near-optimal policy with sample complexity polynomial in the number of latent states, which is significantly smaller than the number of possible observations. Our result gives theoretical justification to the prevailing paradigm of using unsupervised learning for efficient exploration [tang2017exploration,bellemare2016unifying].
Deep Reinforcement Learning with Linear Quadratic Regulator Regions
Feb 26, 2020

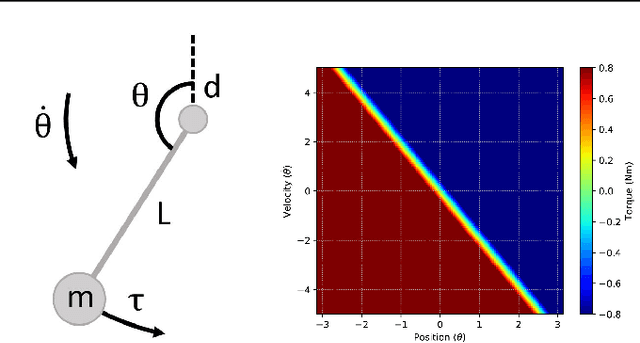
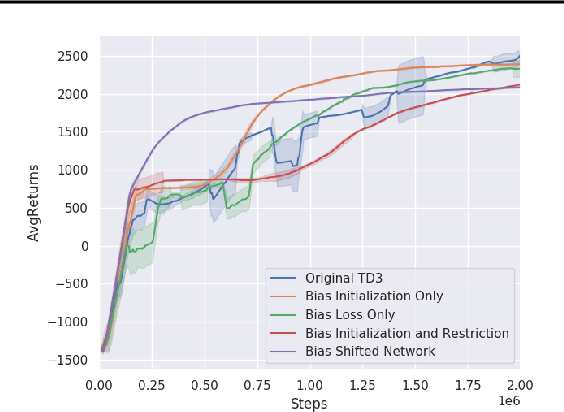
Abstract:Practitioners often rely on compute-intensive domain randomization to ensure reinforcement learning policies trained in simulation can robustly transfer to the real world. Due to unmodeled nonlinearities in the real system, however, even such simulated policies can still fail to perform stably enough to acquire experience in real environments. In this paper we propose a novel method that guarantees a stable region of attraction for the output of a policy trained in simulation, even for highly nonlinear systems. Our core technique is to use "bias-shifted" neural networks for constructing the controller and training the network in the simulator. The modified neural networks not only capture the nonlinearities of the system but also provably preserve linearity in a certain region of the state space and thus can be tuned to resemble a linear quadratic regulator that is known to be stable for the real system. We have tested our new method by transferring simulated policies for a swing-up inverted pendulum to real systems and demonstrated its efficacy.
Sketching Transformed Matrices with Applications to Natural Language Processing
Feb 23, 2020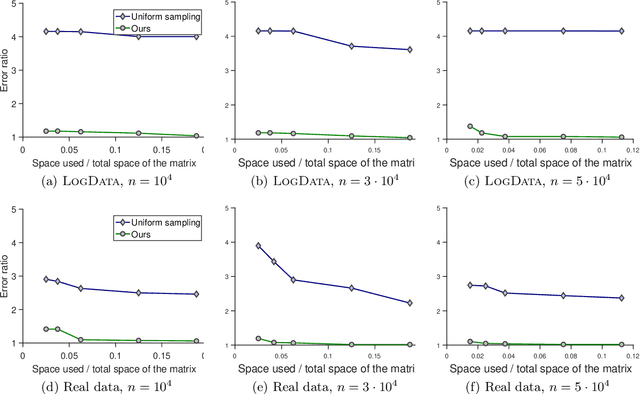
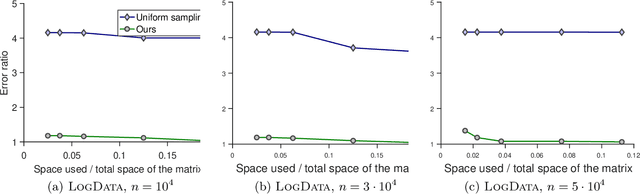
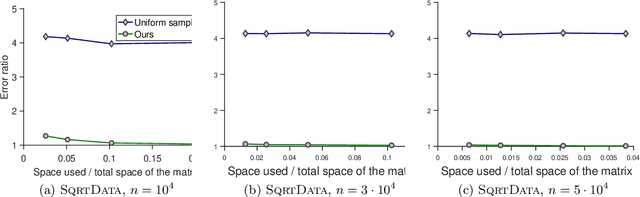
Abstract:Suppose we are given a large matrix $A=(a_{i,j})$ that cannot be stored in memory but is in a disk or is presented in a data stream. However, we need to compute a matrix decomposition of the entry-wisely transformed matrix, $f(A):=(f(a_{i,j}))$ for some function $f$. Is it possible to do it in a space efficient way? Many machine learning applications indeed need to deal with such large transformed matrices, for example word embedding method in NLP needs to work with the pointwise mutual information (PMI) matrix, while the entrywise transformation makes it difficult to apply known linear algebraic tools. Existing approaches for this problem either need to store the whole matrix and perform the entry-wise transformation afterwards, which is space consuming or infeasible, or need to redesign the learning method, which is application specific and requires substantial remodeling. In this paper, we first propose a space-efficient sketching algorithm for computing the product of a given small matrix with the transformed matrix. It works for a general family of transformations with provable small error bounds and thus can be used as a primitive in downstream learning tasks. We then apply this primitive to a concrete application: low-rank approximation. We show that our approach obtains small error and is efficient in both space and time. We complement our theoretical results with experiments on synthetic and real data.
Does Knowledge Transfer Always Help to Learn a Better Policy?
Dec 06, 2019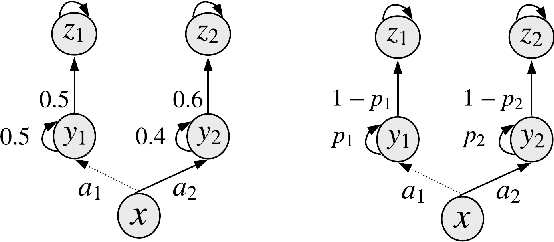
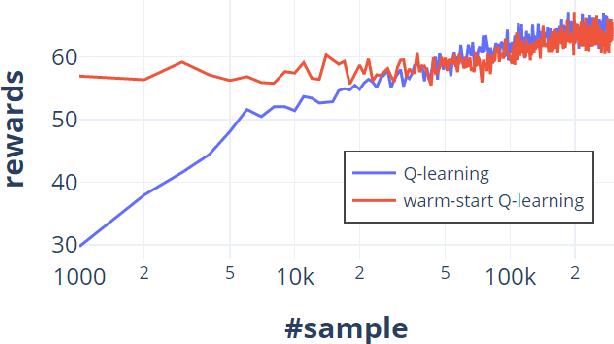
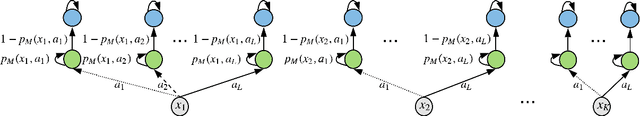
Abstract:One of the key approaches to save samples when learning a policy for a reinforcement learning problem is to use knowledge from an approximate model such as its simulator. However, does knowledge transfer from approximate models always help to learn a better policy? Despite numerous empirical studies of transfer reinforcement learning, an answer to this question is still elusive. In this paper, we provide a strong negative result, showing that even the full knowledge of an approximate model may not help reduce the number of samples for learning an accurate policy of the true model. We construct an example of reinforcement learning models and show that the complexity with or without knowledge transfer has the same order. On the bright side, effective knowledge transferring is still possible under additional assumptions. In particular, we demonstrate that knowing the (linear) bases of the true model significantly reduces the number of samples for learning an accurate policy.
Is a Good Representation Sufficient for Sample Efficient Reinforcement Learning?
Nov 03, 2019
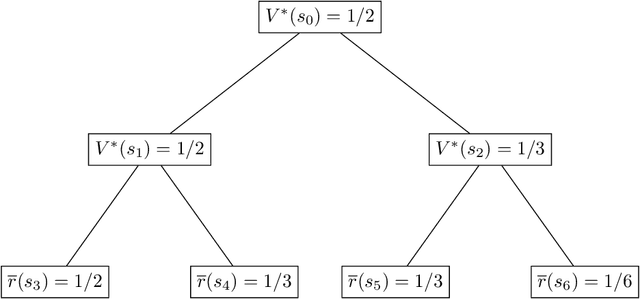
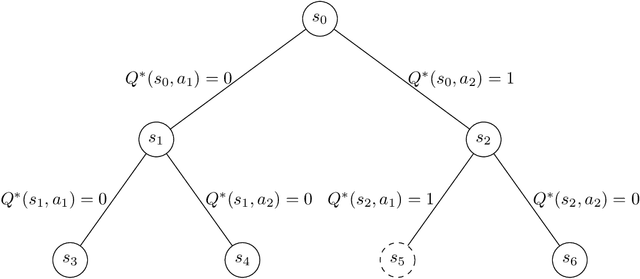
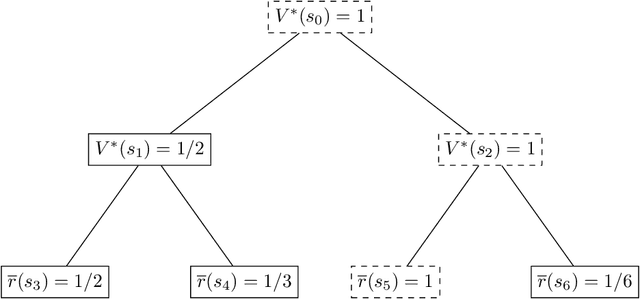
Abstract:Modern deep learning methods provide an effective means to learn good representations. However, is a good representation itself sufficient for efficient reinforcement learning? This question is largely unexplored, and the extant body of literature mainly focuses on conditions which permit efficient reinforcement learning with little understanding of what are necessary conditions for efficient reinforcement learning. This work provides strong negative results for reinforcement learning methods with function approximation for which a good representation (feature extractor) is known to the agent, focusing on natural representational conditions relevant to value-based learning and policy-based learning. For value-based learning, we show that even if the agent has a highly accurate linear representation, the agent still needs to sample exponentially many trajectories in order to find a near-optimal policy. For policy-based learning, we show even if the agent's linear representation is capable of perfectly representing the optimal policy, the agent still needs to sample exponentially many trajectories in order to find a near-optimal policy. These lower bounds highlight the fact that having a good (value-based or policy-based) representation in and of itself is insufficient for efficient reinforcement learning. In particular, these results provide new insights into why the existing provably efficient reinforcement learning methods rely on further assumptions, which are often model-based in nature. Additionally, our lower bounds imply exponential separations in the sample complexity between 1) value-based learning with perfect representation and value-based learning with a good-but-not-perfect representation, 2) value-based learning and policy-based learning, 3) policy-based learning and supervised learning and 4) reinforcement learning and imitation learning.
Continuous Control with Contexts, Provably
Oct 30, 2019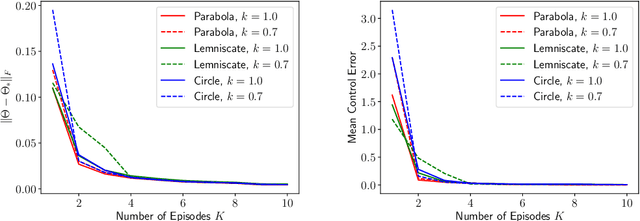
Abstract:A fundamental challenge in artificial intelligence is to build an agent that generalizes and adapts to unseen environments. A common strategy is to build a decoder that takes the context of the unseen new environment as input and generates a policy accordingly. The current paper studies how to build a decoder for the fundamental continuous control task, linear quadratic regulator (LQR), which can model a wide range of real-world physical environments. We present a simple algorithm for this problem, which uses upper confidence bound (UCB) to refine the estimate of the decoder and balance the exploration-exploitation trade-off. Theoretically, our algorithm enjoys a $\widetilde{O}\left(\sqrt{T}\right)$ regret bound in the online setting where $T$ is the number of environments the agent played. This also implies after playing $\widetilde{O}\left(1/\epsilon^2\right)$ environments, the agent is able to transfer the learned knowledge to obtain an $\epsilon$-suboptimal policy for an unseen environment. To our knowledge, this is first provably efficient algorithm to build a decoder in the continuous control setting. While our main focus is theoretical, we also present experiments that demonstrate the effectiveness of our algorithm.
Efficient Symmetric Norm Regression via Linear Sketching
Oct 07, 2019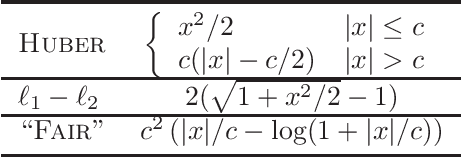

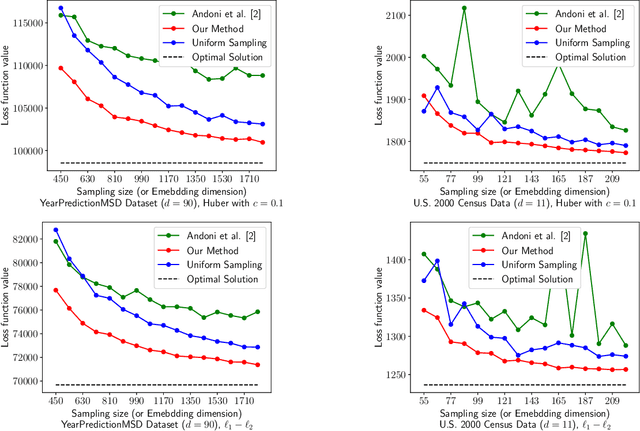
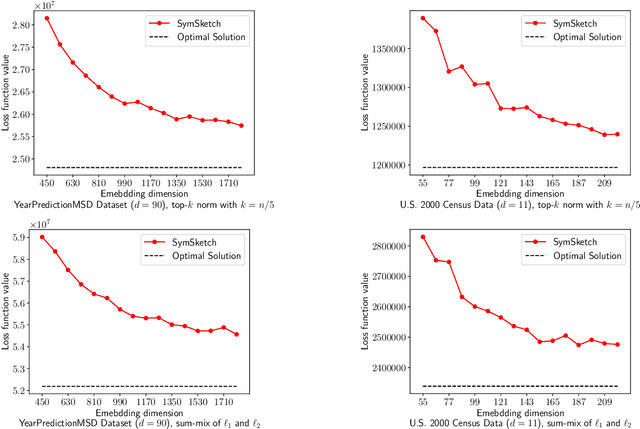
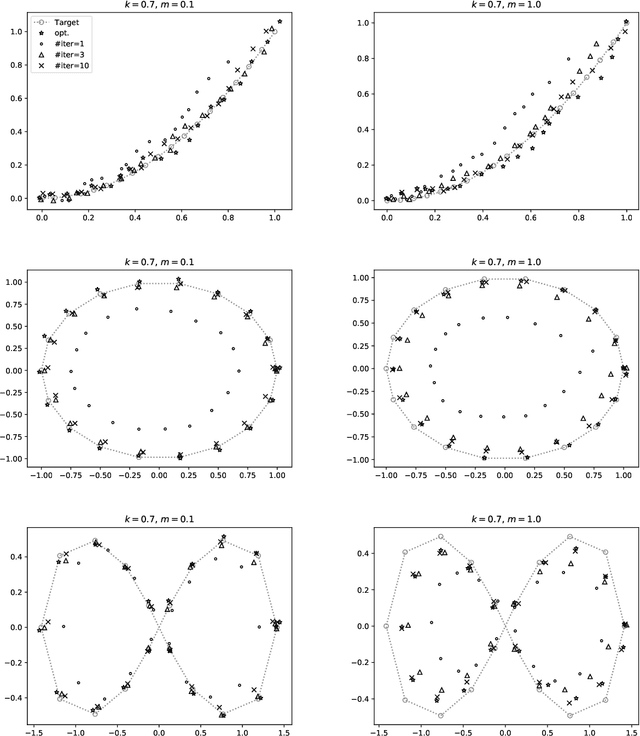
Abstract:We provide efficient algorithms for overconstrained linear regression problems with size $n \times d$ when the loss function is a symmetric norm (a norm invariant under sign-flips and coordinate-permutations). An important class of symmetric norms are Orlicz norms, where for a function $G$ and a vector $y \in \mathbb{R}^n$, the corresponding Orlicz norm $\|y\|_G$ is defined as the unique value $\alpha$ such that $\sum_{i=1}^n G(|y_i|/\alpha) = 1$. When the loss function is an Orlicz norm, our algorithm produces a $(1 + \varepsilon)$-approximate solution for an arbitrarily small constant $\varepsilon > 0$ in input-sparsity time, improving over the previously best-known algorithm which produces a $d \cdot \mathrm{polylog} n$-approximate solution. When the loss function is a general symmetric norm, our algorithm produces a $\sqrt{d} \cdot \mathrm{polylog} n \cdot \mathrm{mmc}(\ell)$-approximate solution in input-sparsity time, where $\mathrm{mmc}(\ell)$ is a quantity related to the symmetric norm under consideration. To the best of our knowledge, this is the first input-sparsity time algorithm with provable guarantees for the general class of symmetric norm regression problem. Our results shed light on resolving the universal sketching problem for linear regression, and the techniques might be of independent interest to numerical linear algebra problems more broadly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge