Explainable and Fine-Grained Safeguarding of LLM Multi-Agent Systems via Bi-Level Graph Anomaly Detection

Large language model (LLM)-based multi-agent systems (MAS) have shown strong capabilities in solving complex tasks. As MAS become increasingly autonomous in various safety-critical tasks, detecting malicious agents has become a critical security concern. Although existing graph anomaly detection (GAD)-based defenses can identify anomalous agents, they mainly rely on coarse sentence-level information and overlook fine-grained lexical cues, leading to suboptimal performance. Moreover, the lack of interpretability in these methods limits their reliability and real-world applicability. To address these limitations, we propose XG-Guard, an explainable and fine-grained safeguarding framework for detecting malicious agents in MAS. To incorporate both coarse and fine-grained textual information for anomalous agent identification, we utilize a bi-level agent encoder to jointly model the sentence- and token-level representations of each agent. A theme-based anomaly detector further captures the evolving discussion focus in MAS dialogues, while a bi-level score fusion mechanism quantifies token-level contributions for explanation. Extensive experiments across diverse MAS topologies and attack scenarios demonstrate robust detection performance and strong interpretability of XG-Guard.

Correcting False Alarms from Unseen: Adapting Graph Anomaly Detectors at Test Time

Graph anomaly detection (GAD), which aims to detect outliers in graph-structured data, has received increasing research attention recently. However, existing GAD methods assume identical training and testing distributions, which is rarely valid in practice. In real-world scenarios, unseen but normal samples may emerge during deployment, leading to a normality shift that degrades the performance of GAD models trained on the original data. Through empirical analysis, we reveal that the degradation arises from (1) semantic confusion, where unseen normal samples are misinterpreted as anomalies due to their novel patterns, and (2) aggregation contamination, where the representations of seen normal nodes are distorted by unseen normals through message aggregation. While retraining or fine-tuning GAD models could be a potential solution to the above challenges, the high cost of model retraining and the difficulty of obtaining labeled data often render this approach impractical in real-world applications. To bridge the gap, we proposed a lightweight and plug-and-play Test-time adaptation framework for correcting Unseen Normal pattErns (TUNE) in GAD. To address semantic confusion, a graph aligner is employed to align the shifted data to the original one at the graph attribute level. Moreover, we utilize the minimization of representation-level shift as a supervision signal to train the aligner, which leverages the estimated aggregation contamination as a key indicator of normality shift. Extensive experiments on 10 real-world datasets demonstrate that TUNE significantly enhances the generalizability of pre-trained GAD models to both synthetic and real unseen normal patterns.

A Provably-Correct and Robust Convex Model for Smooth Separable NMF

Nonnegative matrix factorization (NMF) is a linear dimensionality reduction technique for nonnegative data, with applications such as hyperspectral unmixing and topic modeling. NMF is a difficult problem in general (NP-hard), and its solutions are typically not unique. To address these two issues, additional constraints or assumptions are often used. In particular, separability assumes that the basis vectors in the NMF are equal to some columns of the input matrix. In that case, the problem is referred to as separable NMF (SNMF) and can be solved in polynomial-time with robustness guarantees, while identifying a unique solution. However, in real-world scenarios, due to noise or variability, multiple data points may lie near the basis vectors, which SNMF does not leverage. In this work, we rely on the smooth separability assumption, which assumes that each basis vector is close to multiple data points. We explore the properties of the corresponding problem, referred to as smooth SNMF (SSNMF), and examine how it relates to SNMF and orthogonal NMF. We then propose a convex model for SSNMF and show that it provably recovers the sought-after factors, even in the presence of noise. We finally adapt an existing fast gradient method to solve this convex model for SSNMF, and show that it compares favorably with state-of-the-art methods on both synthetic and hyperspectral datasets.

AU-Blendshape for Fine-grained Stylized 3D Facial Expression Manipulation

While 3D facial animation has made impressive progress, challenges still exist in realizing fine-grained stylized 3D facial expression manipulation due to the lack of appropriate datasets. In this paper, we introduce the AUBlendSet, a 3D facial dataset based on AU-Blendshape representation for fine-grained facial expression manipulation across identities. AUBlendSet is a blendshape data collection based on 32 standard facial action units (AUs) across 500 identities, along with an additional set of facial postures annotated with detailed AUs. Based on AUBlendSet, we propose AUBlendNet to learn AU-Blendshape basis vectors for different character styles. AUBlendNet predicts, in parallel, the AU-Blendshape basis vectors of the corresponding style for a given identity mesh, thereby achieving stylized 3D emotional facial manipulation. We comprehensively validate the effectiveness of AUBlendSet and AUBlendNet through tasks such as stylized facial expression manipulation, speech-driven emotional facial animation, and emotion recognition data augmentation. Through a series of qualitative and quantitative experiments, we demonstrate the potential and importance of AUBlendSet and AUBlendNet in 3D facial animation tasks. To the best of our knowledge, AUBlendSet is the first dataset, and AUBlendNet is the first network for continuous 3D facial expression manipulation for any identity through facial AUs. Our source code is available at https://github.com/wslh852/AUBlendNet.git.

Wav2Sem: Plug-and-Play Audio Semantic Decoupling for 3D Speech-Driven Facial Animation

In 3D speech-driven facial animation generation, existing methods commonly employ pre-trained self-supervised audio models as encoders. However, due to the prevalence of phonetically similar syllables with distinct lip shapes in language, these near-homophone syllables tend to exhibit significant coupling in self-supervised audio feature spaces, leading to the averaging effect in subsequent lip motion generation. To address this issue, this paper proposes a plug-and-play semantic decorrelation module-Wav2Sem. This module extracts semantic features corresponding to the entire audio sequence, leveraging the added semantic information to decorrelate audio encodings within the feature space, thereby achieving more expressive audio features. Extensive experiments across multiple Speech-driven models indicate that the Wav2Sem module effectively decouples audio features, significantly alleviating the averaging effect of phonetically similar syllables in lip shape generation, thereby enhancing the precision and naturalness of facial animations. Our source code is available at https://github.com/wslh852/Wav2Sem.git.

A Label-Free Heterophily-Guided Approach for Unsupervised Graph Fraud Detection

Graph fraud detection (GFD) has rapidly advanced in protecting online services by identifying malicious fraudsters. Recent supervised GFD research highlights that heterophilic connections between fraudsters and users can greatly impact detection performance, since fraudsters tend to camouflage themselves by building more connections to benign users. Despite the promising performance of supervised GFD methods, the reliance on labels limits their applications to unsupervised scenarios; Additionally, accurately capturing complex and diverse heterophily patterns without labels poses a further challenge. To fill the gap, we propose a Heterophily-guided Unsupervised Graph fraud dEtection approach (HUGE) for unsupervised GFD, which contains two essential components: a heterophily estimation module and an alignment-based fraud detection module. In the heterophily estimation module, we design a novel label-free heterophily metric called HALO, which captures the critical graph properties for GFD, enabling its outstanding ability to estimate heterophily from node attributes. In the alignment-based fraud detection module, we develop a joint MLP-GNN architecture with ranking loss and asymmetric alignment loss. The ranking loss aligns the predicted fraud score with the relative order of HALO, providing an extra robustness guarantee by comparing heterophily among non-adjacent nodes. Moreover, the asymmetric alignment loss effectively utilizes structural information while alleviating the feature-smooth effects of GNNs.Extensive experiments on 6 datasets demonstrate that HUGE significantly outperforms competitors, showcasing its effectiveness and robustness. The source code of HUGE is at https://github.com/CampanulaBells/HUGE-GAD.

Non-Negative Reduced Biquaternion Matrix Factorization with Applications in Color Face Recognition

Reduced biquaternion (RB), as a four-dimensional algebra highly suitable for representing color pixels, has recently garnered significant attention from numerous scholars. In this paper, for color image processing problems, we introduce a concept of the non-negative RB matrix and then use the multiplication properties of RB to propose a non-negative RB matrix factorization (NRBMF) model. The NRBMF model is introduced to address the challenge of reasonably establishing a non-negative quaternion matrix factorization model, which is primarily hindered by the multiplication properties of traditional quaternions. Furthermore, this paper transforms the problem of solving the NRBMF model into an RB alternating non-negative least squares (RB-ANNLS) problem. Then, by introducing a method to compute the gradient of the real function with RB matrix variables, we solve the RB-ANNLS optimization problem using the RB projected gradient algorithm and conduct a convergence analysis of the algorithm. Finally, we validate the effectiveness and superiority of the proposed NRBMF model in color face recognition.

PREM: A Simple Yet Effective Approach for Node-Level Graph Anomaly Detection

Node-level graph anomaly detection (GAD) plays a critical role in identifying anomalous nodes from graph-structured data in various domains such as medicine, social networks, and e-commerce. However, challenges have arisen due to the diversity of anomalies and the dearth of labeled data. Existing methodologies - reconstruction-based and contrastive learning - while effective, often suffer from efficiency issues, stemming from their complex objectives and elaborate modules. To improve the efficiency of GAD, we introduce a simple method termed PREprocessing and Matching (PREM for short). Our approach streamlines GAD, reducing time and memory consumption while maintaining powerful anomaly detection capabilities. Comprising two modules - a pre-processing module and an ego-neighbor matching module - PREM eliminates the necessity for message-passing propagation during training, and employs a simple contrastive loss, leading to considerable reductions in training time and memory usage. Moreover, through rigorous evaluations of five real-world datasets, our method demonstrated robustness and effectiveness. Notably, when validated on the ACM dataset, PREM achieved a 5% improvement in AUC, a 9-fold increase in training speed, and sharply reduce memory usage compared to the most efficient baseline.

Separable Quaternion Matrix Factorization for Polarization Images

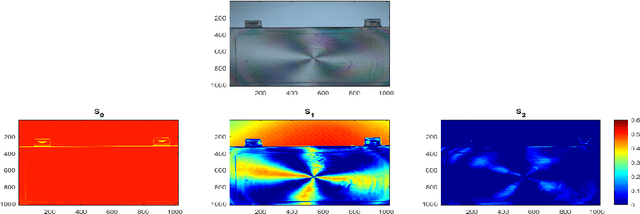
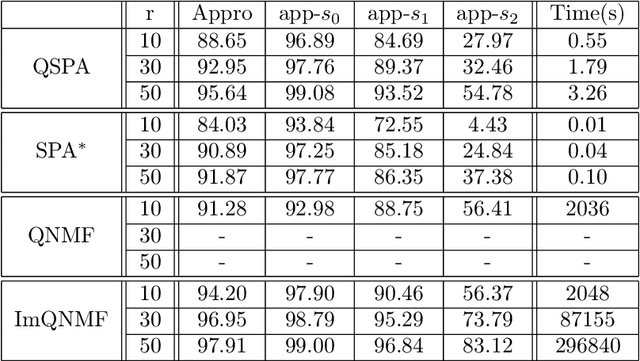
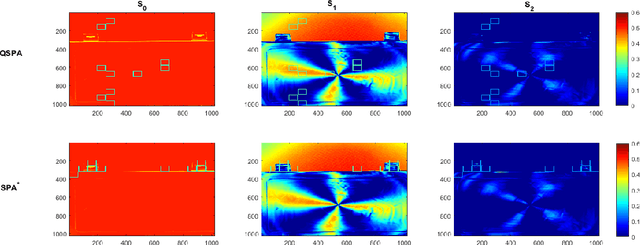
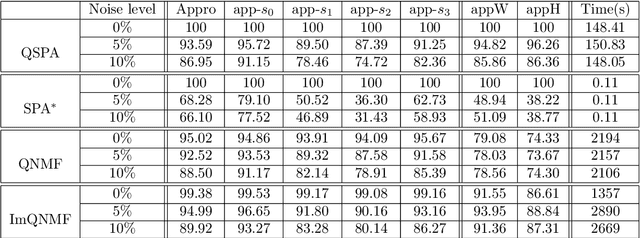
Polarization is a unique characteristic of transverse wave and is represented by Stokes parameters. Analysis of polarization states can reveal valuable information about the sources. In this paper, we propose a separable low-rank quaternion linear mixing model to polarized signals: we assume each column of the source factor matrix equals a column of polarized data matrix and refer to the corresponding problem as separable quaternion matrix factorization (SQMF). We discuss some properties of the matrix that can be decomposed by SQMF. To determine the source factor matrix in quaternion space, we propose a heuristic algorithm called quaternion successive projection algorithm (QSPA) inspired by the successive projection algorithm. To guarantee the effectiveness of QSPA, a new normalization operator is proposed for the quaternion matrix. We use a block coordinate descent algorithm to compute nonnegative factor activation matrix in real number space. We test our method on the applications of polarization image representation and spectro-polarimetric imaging unmixing to verify its effectiveness.

Diverse Dance Synthesis via Keyframes with Transformer Controllers

Existing keyframe-based motion synthesis mainly focuses on the generation of cyclic actions or short-term motion, such as walking, running, and transitions between close postures. However, these methods will significantly degrade the naturalness and diversity of the synthesized motion when dealing with complex and impromptu movements, e.g., dance performance and martial arts. In addition, current research lacks fine-grained control over the generated motion, which is essential for intelligent human-computer interaction and animation creation. In this paper, we propose a novel keyframe-based motion generation network based on multiple constraints, which can achieve diverse dance synthesis via learned knowledge. Specifically, the algorithm is mainly formulated based on the recurrent neural network (RNN) and the Transformer architecture. The backbone of our network is a hierarchical RNN module composed of two long short-term memory (LSTM) units, in which the first LSTM is utilized to embed the posture information of the historical frames into a latent space, and the second one is employed to predict the human posture for the next frame. Moreover, our framework contains two Transformer-based controllers, which are used to model the constraints of the root trajectory and the velocity factor respectively, so as to better utilize the temporal context of the frames and achieve fine-grained motion control. We verify the proposed approach on a dance dataset containing a wide range of contemporary dance. The results of three quantitative analyses validate the superiority of our algorithm. The video and qualitative experimental results demonstrate that the complex motion sequences generated by our algorithm can achieve diverse and smooth motion transitions between keyframes, even for long-term synthesis.