Efficient Low-Tubal-Rank Tensor Estimation via Alternating Preconditioned Gradient Descent

The problem of low-tubal-rank tensor estimation is a fundamental task with wide applications across high-dimensional signal processing, machine learning, and image science. Traditional approaches tackle such a problem by performing tensor singular value decomposition, which is computationally expensive and becomes infeasible for large-scale tensors. Recent approaches address this issue by factorizing the tensor into two smaller factor tensors and solving the resulting problem using gradient descent. However, this kind of approach requires an accurate estimate of the tensor rank, and when the rank is overestimated, the convergence of gradient descent and its variants slows down significantly or even diverges. To address this problem, we propose an Alternating Preconditioned Gradient Descent (APGD) algorithm, which accelerates convergence in the over-parameterized setting by adding a preconditioning term to the original gradient and updating these two factors alternately. Based on certain geometric assumptions on the objective function, we establish linear convergence guarantees for more general low-tubal-rank tensor estimation problems. Then we further analyze the specific cases of low-tubal-rank tensor factorization and low-tubal-rank tensor recovery. Our theoretical results show that APGD achieves linear convergence even under over-parameterization, and the convergence rate is independent of the tensor condition number. Extensive simulations on synthetic data are carried out to validate our theoretical assertions.

Spectral Algorithms under Covariate Shift

Spectral algorithms leverage spectral regularization techniques to analyze and process data, providing a flexible framework for addressing supervised learning problems. To deepen our understanding of their performance in real-world scenarios where the distributions of training and test data may differ, we conduct a rigorous investigation into the convergence behavior of spectral algorithms under distribution shifts, specifically within the framework of reproducing kernel Hilbert spaces. Our study focuses on the case of covariate shift. In this scenario, the marginal distributions of the input data differ between the training and test datasets, while the conditional distribution of the output given the input remains unchanged. Under this setting, we analyze the generalization error of spectral algorithms and show that they achieve minimax optimality when the density ratios between the training and test distributions are uniformly bounded. However, we also identify a critical limitation: when the density ratios are unbounded, the spectral algorithms may become suboptimal. To address this limitation, we propose a weighted spectral algorithm that incorporates density ratio information into the learning process. Our theoretical analysis shows that this weighted approach achieves optimal capacity-independent convergence rates. Furthermore, by introducing a weight clipping technique, we demonstrate that the convergence rates of the weighted spectral algorithm can approach the optimal capacity-dependent convergence rates arbitrarily closely. This improvement resolves the suboptimality issue in unbounded density ratio scenarios and advances the state-of-the-art by refining existing theoretical results.

ScalingNote: Scaling up Retrievers with Large Language Models for Real-World Dense Retrieval

Dense retrieval in most industries employs dual-tower architectures to retrieve query-relevant documents. Due to online deployment requirements, existing real-world dense retrieval systems mainly enhance performance by designing negative sampling strategies, overlooking the advantages of scaling up. Recently, Large Language Models (LLMs) have exhibited superior performance that can be leveraged for scaling up dense retrieval. However, scaling up retrieval models significantly increases online query latency. To address this challenge, we propose ScalingNote, a two-stage method to exploit the scaling potential of LLMs for retrieval while maintaining online query latency. The first stage is training dual towers, both initialized from the same LLM, to unlock the potential of LLMs for dense retrieval. Then, we distill only the query tower using mean squared error loss and cosine similarity to reduce online costs. Through theoretical analysis and comprehensive offline and online experiments, we show the effectiveness and efficiency of ScalingNote. Our two-stage scaling method outperforms end-to-end models and verifies the scaling law of dense retrieval with LLMs in industrial scenarios, enabling cost-effective scaling of dense retrieval systems. Our online method incorporating ScalingNote significantly enhances the relevance between retrieved documents and queries.

MA4DIV: Multi-Agent Reinforcement Learning for Search Result Diversification

The objective of search result diversification (SRD) is to ensure that selected documents cover as many different subtopics as possible. Existing methods primarily utilize a paradigm of "greedy selection", i.e., selecting one document with the highest diversity score at a time. These approaches tend to be inefficient and are easily trapped in a suboptimal state. In addition, some other methods aim to approximately optimize the diversity metric, such as $\alpha$-NDCG, but the results still remain suboptimal. To address these challenges, we introduce Multi-Agent reinforcement learning (MARL) for search result DIVersity, which called MA4DIV. In this approach, each document is an agent and the search result diversification is modeled as a cooperative task among multiple agents. This approach allows for directly optimizing the diversity metrics, such as $\alpha$-NDCG, while achieving high training efficiency. We conducted preliminary experiments on public TREC datasets to demonstrate the effectiveness and potential of MA4DIV. Considering the limited number of queries in public TREC datasets, we construct a large-scale dataset from industry sources and show that MA4DIV achieves substantial improvements in both effectiveness and efficiency than existing baselines on a industrial scale dataset.

Nonlinear functional regression by functional deep neural network with kernel embedding

With the rapid development of deep learning in various fields of science and technology, such as speech recognition, image classification, and natural language processing, recently it is also widely applied in the functional data analysis (FDA) with some empirical success. However, due to the infinite dimensional input, we need a powerful dimension reduction method for functional learning tasks, especially for the nonlinear functional regression. In this paper, based on the idea of smooth kernel integral transformation, we propose a functional deep neural network with an efficient and fully data-dependent dimension reduction method. The architecture of our functional net consists of a kernel embedding step: an integral transformation with a data-dependent smooth kernel; a projection step: a dimension reduction by projection with eigenfunction basis based on the embedding kernel; and finally an expressive deep ReLU neural network for the prediction. The utilization of smooth kernel embedding enables our functional net to be discretization invariant, efficient, and robust to noisy observations, capable of utilizing information in both input functions and responses data, and have a low requirement on the number of discrete points for an unimpaired generalization performance. We conduct theoretical analysis including approximation error and generalization error analysis, and numerical simulations to verify these advantages of our functional net.

Distributed Gradient Descent for Functional Learning

In recent years, different types of distributed learning schemes have received increasing attention for their strong advantages in handling large-scale data information. In the information era, to face the big data challenges which stem from functional data analysis very recently, we propose a novel distributed gradient descent functional learning (DGDFL) algorithm to tackle functional data across numerous local machines (processors) in the framework of reproducing kernel Hilbert space. Based on integral operator approaches, we provide the first theoretical understanding of the DGDFL algorithm in many different aspects in the literature. On the way of understanding DGDFL, firstly, a data-based gradient descent functional learning (GDFL) algorithm associated with a single-machine model is proposed and comprehensively studied. Under mild conditions, confidence-based optimal learning rates of DGDFL are obtained without the saturation boundary on the regularity index suffered in previous works in functional regression. We further provide a semi-supervised DGDFL approach to weaken the restriction on the maximal number of local machines to ensure optimal rates. To our best knowledge, the DGDFL provides the first distributed iterative training approach to functional learning and enriches the stage of functional data analysis.

Approximation of Nonlinear Functionals Using Deep ReLU Networks

In recent years, functional neural networks have been proposed and studied in order to approximate nonlinear continuous functionals defined on $L^p([-1, 1]^s)$ for integers $s\ge1$ and $1\le p<\infty$. However, their theoretical properties are largely unknown beyond universality of approximation or the existing analysis does not apply to the rectified linear unit (ReLU) activation function. To fill in this void, we investigate here the approximation power of functional deep neural networks associated with the ReLU activation function by constructing a continuous piecewise linear interpolation under a simple triangulation. In addition, we establish rates of approximation of the proposed functional deep ReLU networks under mild regularity conditions. Finally, our study may also shed some light on the understanding of functional data learning algorithms.

PILE: Pairwise Iterative Logits Ensemble for Multi-Teacher Labeled Distillation

Pre-trained language models have become a crucial part of ranking systems and achieved very impressive effects recently. To maintain high performance while keeping efficient computations, knowledge distillation is widely used. In this paper, we focus on two key questions in knowledge distillation for ranking models: 1) how to ensemble knowledge from multi-teacher; 2) how to utilize the label information of data in the distillation process. We propose a unified algorithm called Pairwise Iterative Logits Ensemble (PILE) to tackle these two questions simultaneously. PILE ensembles multi-teacher logits supervised by label information in an iterative way and achieved competitive performance in both offline and online experiments. The proposed method has been deployed in a real-world commercial search system.

Optimal prediction for kernel-based semi-functional linear regression

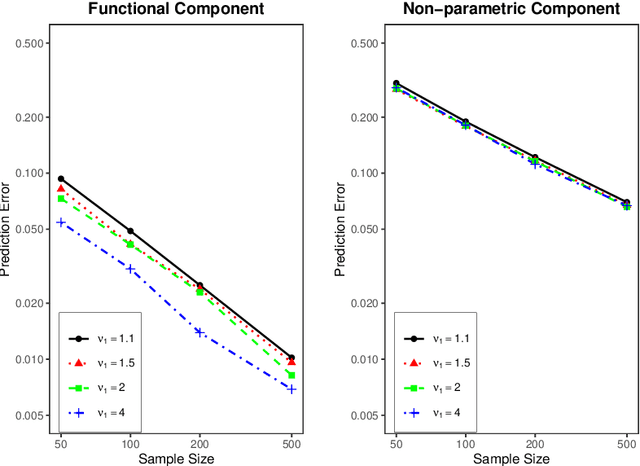
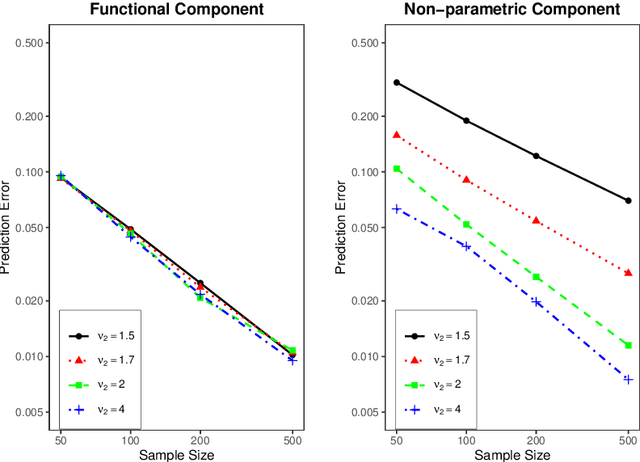
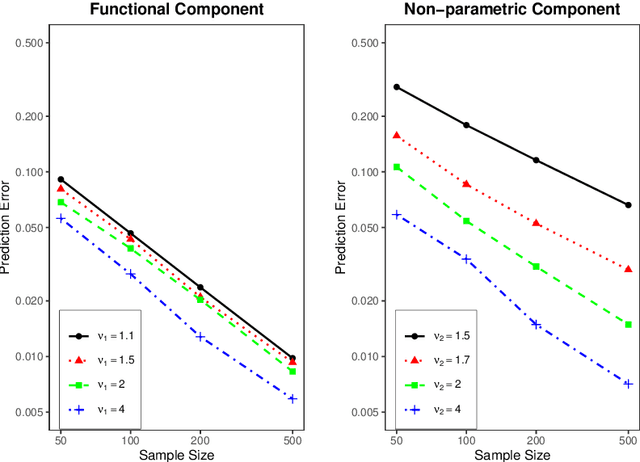
In this paper, we establish minimax optimal rates of convergence for prediction in a semi-functional linear model that consists of a functional component and a less smooth nonparametric component. Our results reveal that the smoother functional component can be learned with the minimax rate as if the nonparametric component were known. More specifically, a double-penalized least squares method is adopted to estimate both the functional and nonparametric components within the framework of reproducing kernel Hilbert spaces. By virtue of the representer theorem, an efficient algorithm that requires no iterations is proposed to solve the corresponding optimization problem, where the regularization parameters are selected by the generalized cross validation criterion. Numerical studies are provided to demonstrate the effectiveness of the method and to verify the theoretical analysis.

Comparison theorems on large-margin learning

This paper studies binary classification problem associated with a family of loss functions called large-margin unified machines (LUM), which offers a natural bridge between distribution-based likelihood approaches and margin-based approaches. It also can overcome the so-called data piling issue of support vector machine in the high-dimension and low-sample size setting. In this paper we establish some new comparison theorems for all LUM loss functions which play a key role in the further error analysis of large-margin learning algorithms.