A Fully Single Loop Algorithm for Bilevel Optimization without Hessian Inverse

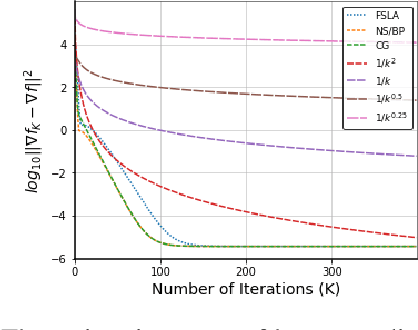
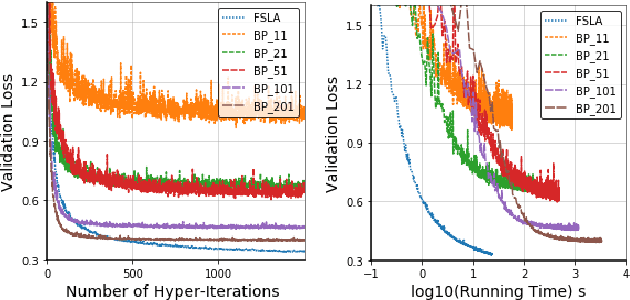
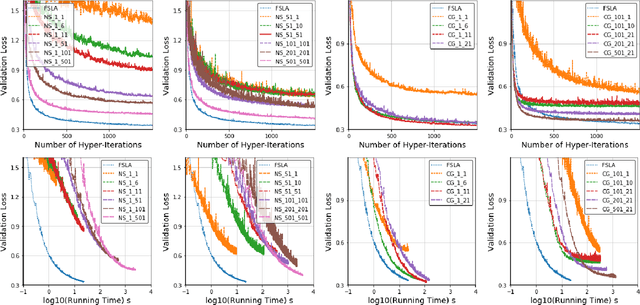
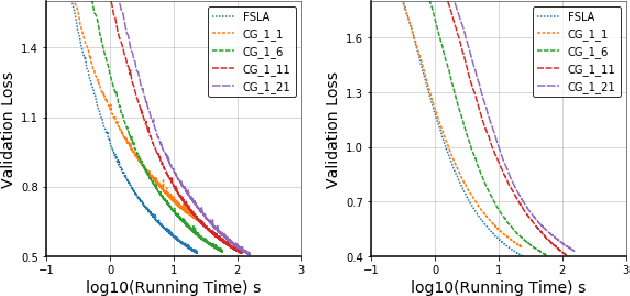
In this paper, we propose a new Hessian inverse free Fully Single Loop Algorithm (FSLA) for bilevel optimization problems. Classic algorithms for bilevel optimization admit a double loop structure which is computationally expensive. Recently, several single loop algorithms have been proposed with optimizing the inner and outer variable alternatively. However, these algorithms not yet achieve fully single loop. As they overlook the loop needed to evaluate the hyper-gradient for a given inner and outer state. In order to develop a fully single loop algorithm, we first study the structure of the hyper-gradient and identify a general approximation formulation of hyper-gradient computation that encompasses several previous common approaches, e.g. back-propagation through time, conjugate gradient, \emph{etc.} Based on this formulation, we introduce a new state variable to maintain the historical hyper-gradient information. Combining our new formulation with the alternative update of the inner and outer variables, we propose an efficient fully single loop algorithm. We theoretically show that the error generated by the new state can be bounded and our algorithm converges with the rate of $O(\epsilon^{-2})$. Finally, we verify the efficacy our algorithm empirically through multiple bilevel optimization based machine learning tasks.

Adaptive Hierarchical Similarity Metric Learning with Noisy Labels

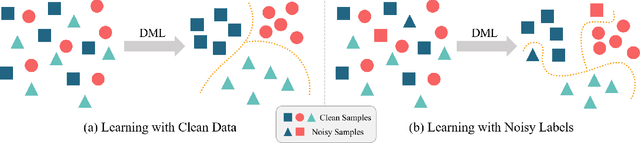
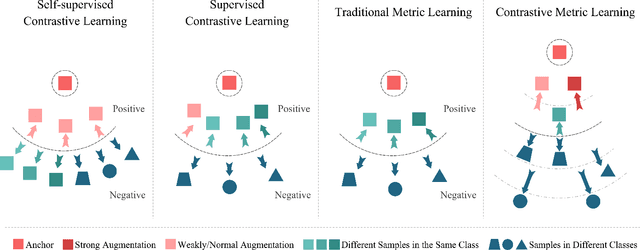
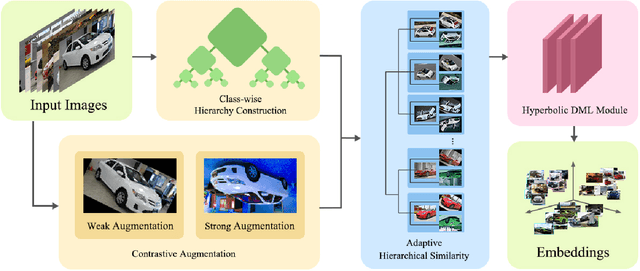
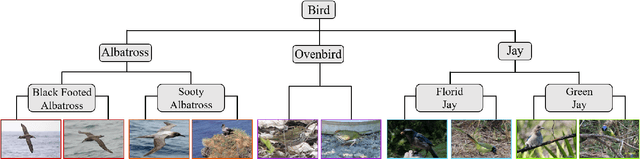
Deep Metric Learning (DML) plays a critical role in various machine learning tasks. However, most existing deep metric learning methods with binary similarity are sensitive to noisy labels, which are widely present in real-world data. Since these noisy labels often cause severe performance degradation, it is crucial to enhance the robustness and generalization ability of DML. In this paper, we propose an Adaptive Hierarchical Similarity Metric Learning method. It considers two noise-insensitive information, \textit{i.e.}, class-wise divergence and sample-wise consistency. Specifically, class-wise divergence can effectively excavate richer similarity information beyond binary in modeling by taking advantage of Hyperbolic metric learning, while sample-wise consistency can further improve the generalization ability of the model using contrastive augmentation. More importantly, we design an adaptive strategy to integrate this information in a unified view. It is noteworthy that the new method can be extended to any pair-based metric loss. Extensive experimental results on benchmark datasets demonstrate that our method achieves state-of-the-art performance compared with current deep metric learning approaches.

AsySQN: Faster Vertical Federated Learning Algorithms with Better Computation Resource Utilization

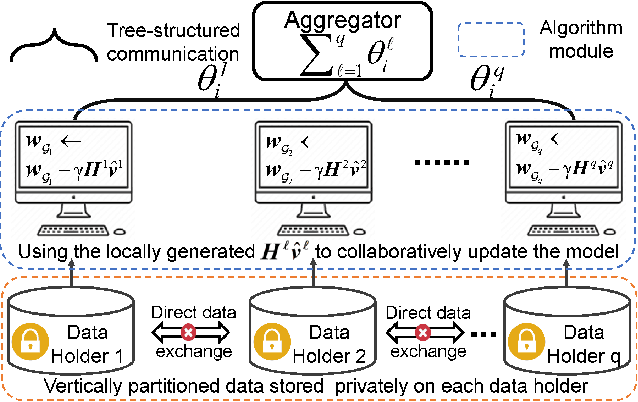
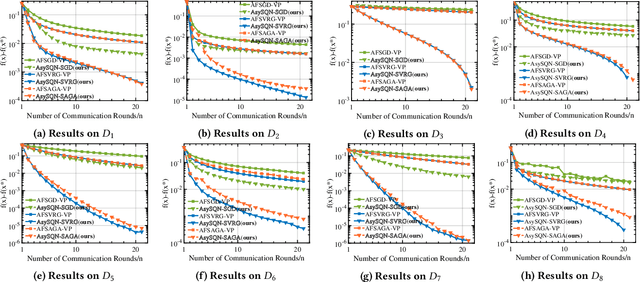
Vertical federated learning (VFL) is an effective paradigm of training the emerging cross-organizational (e.g., different corporations, companies and organizations) collaborative learning with privacy preserving. Stochastic gradient descent (SGD) methods are the popular choices for training VFL models because of the low per-iteration computation. However, existing SGD-based VFL algorithms are communication-expensive due to a large number of communication rounds. Meanwhile, most existing VFL algorithms use synchronous computation which seriously hamper the computation resource utilization in real-world applications. To address the challenges of communication and computation resource utilization, we propose an asynchronous stochastic quasi-Newton (AsySQN) framework for VFL, under which three algorithms, i.e. AsySQN-SGD, -SVRG and -SAGA, are proposed. The proposed AsySQN-type algorithms making descent steps scaled by approximate (without calculating the inverse Hessian matrix explicitly) Hessian information convergence much faster than SGD-based methods in practice and thus can dramatically reduce the number of communication rounds. Moreover, the adopted asynchronous computation can make better use of the computation resource. We theoretically prove the convergence rates of our proposed algorithms for strongly convex problems. Extensive numerical experiments on real-word datasets demonstrate the lower communication costs and better computation resource utilization of our algorithms compared with state-of-the-art VFL algorithms.

An Accelerated Variance-Reduced Conditional Gradient Sliding Algorithm for First-order and Zeroth-order Optimization

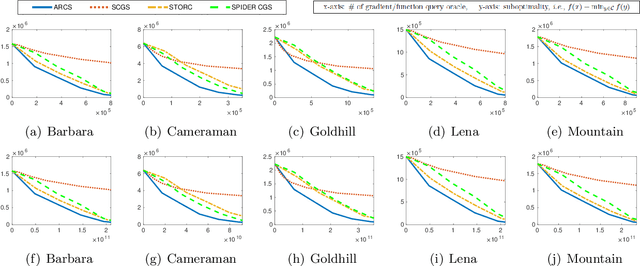
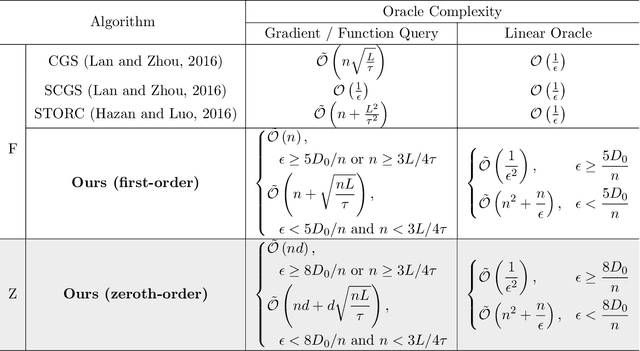
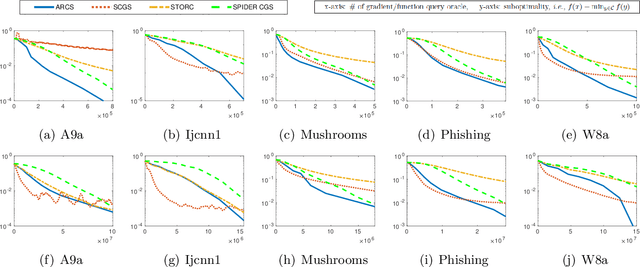
The conditional gradient algorithm (also known as the Frank-Wolfe algorithm) has recently regained popularity in the machine learning community due to its projection-free property to solve constrained problems. Although many variants of the conditional gradient algorithm have been proposed to improve performance, they depend on first-order information (gradient) to optimize. Naturally, these algorithms are unable to function properly in the field of increasingly popular zeroth-order optimization, where only zeroth-order information (function value) is available. To fill in this gap, we propose a novel Accelerated variance-Reduced Conditional gradient Sliding (ARCS) algorithm for finite-sum problems, which can use either first-order or zeroth-order information to optimize. To the best of our knowledge, ARCS is the first zeroth-order conditional gradient sliding type algorithms solving convex problems in zeroth-order optimization. In first-order optimization, the convergence results of ARCS substantially outperform previous algorithms in terms of the number of gradient query oracle. Finally we validated the superiority of ARCS by experiments on real-world datasets.

DSNet: A Dual-Stream Framework for Weakly-Supervised Gigapixel Pathology Image Analysis

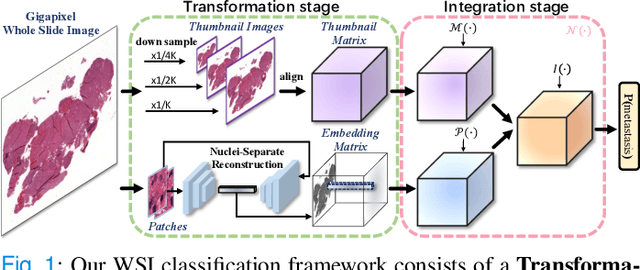
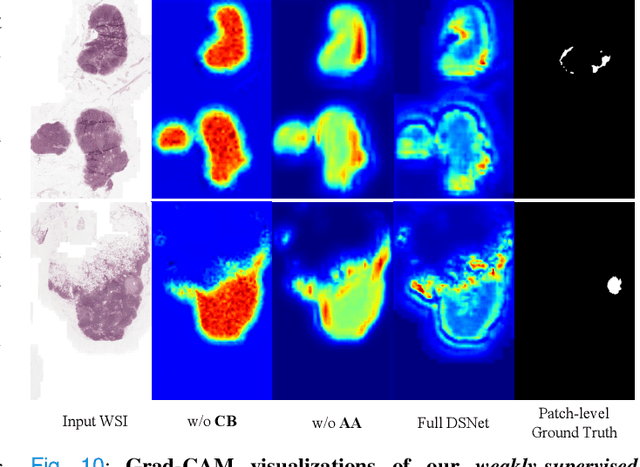
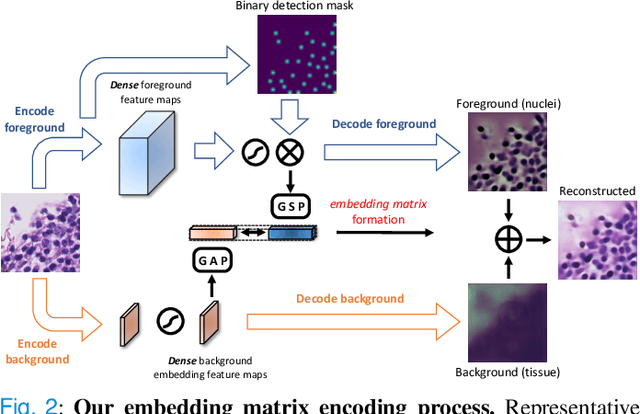
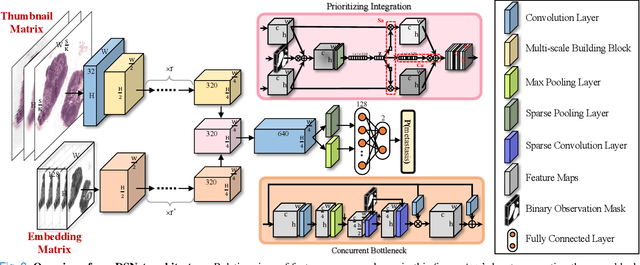
We present a novel weakly-supervised framework for classifying whole slide images (WSIs). WSIs, due to their gigapixel resolution, are commonly processed by patch-wise classification with patch-level labels. However, patch-level labels require precise annotations, which is expensive and usually unavailable on clinical data. With image-level labels only, patch-wise classification would be sub-optimal due to inconsistency between the patch appearance and image-level label. To address this issue, we posit that WSI analysis can be effectively conducted by integrating information at both high magnification (local) and low magnification (regional) levels. We auto-encode the visual signals in each patch into a latent embedding vector representing local information, and down-sample the raw WSI to hardware-acceptable thumbnails representing regional information. The WSI label is then predicted with a Dual-Stream Network (DSNet), which takes the transformed local patch embeddings and multi-scale thumbnail images as inputs and can be trained by the image-level label only. Experiments conducted on two large-scale public datasets demonstrate that our method outperforms all recent state-of-the-art weakly-supervised WSI classification methods.

PSGR: Pixel-wise Sparse Graph Reasoning for COVID-19 Pneumonia Segmentation in CT Images

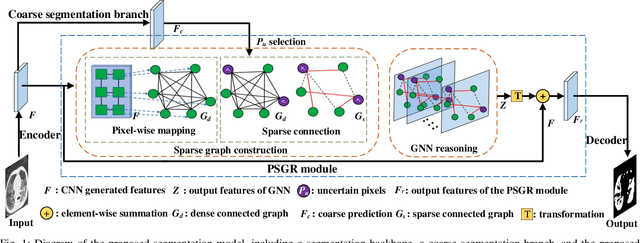
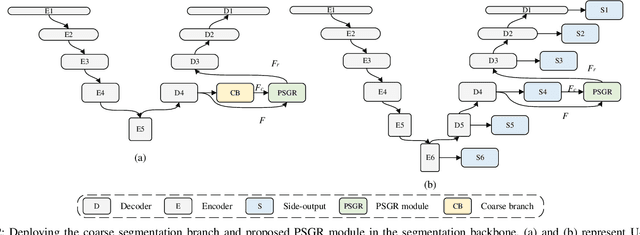
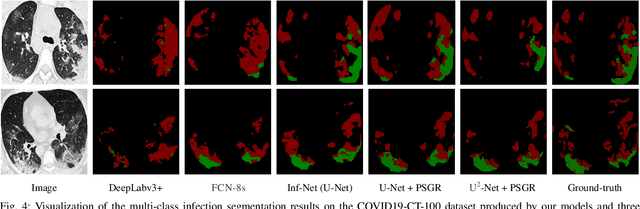
Automated and accurate segmentation of the infected regions in computed tomography (CT) images is critical for the prediction of the pathological stage and treatment response of COVID-19. Several deep convolutional neural networks (DCNNs) have been designed for this task, whose performance, however, tends to be suppressed by their limited local receptive fields and insufficient global reasoning ability. In this paper, we propose a pixel-wise sparse graph reasoning (PSGR) module and insert it into a segmentation network to enhance the modeling of long-range dependencies for COVID-19 infected region segmentation in CT images. In the PSGR module, a graph is first constructed by projecting each pixel on a node based on the features produced by the segmentation backbone, and then converted into a sparsely-connected graph by keeping only K strongest connections to each uncertain pixel. The long-range information reasoning is performed on the sparsely-connected graph to generate enhanced features. The advantages of this module are two-fold: (1) the pixel-wise mapping strategy not only avoids imprecise pixel-to-node projections but also preserves the inherent information of each pixel for global reasoning; and (2) the sparsely-connected graph construction results in effective information retrieval and reduction of the noise propagation. The proposed solution has been evaluated against four widely-used segmentation models on three public datasets. The results show that the segmentation model equipped with our PSGR module can effectively segment COVID-19 infected regions in CT images, outperforming all other competing models.

Boundary-aware Graph Reasoning for Semantic Segmentation

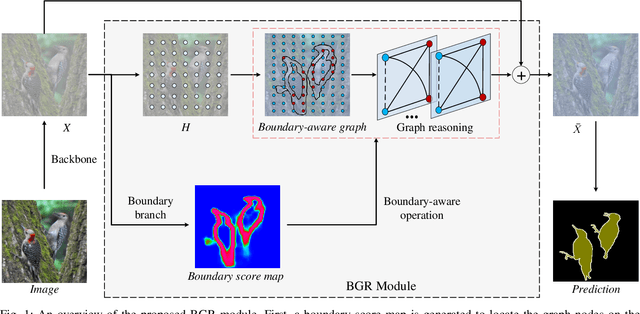
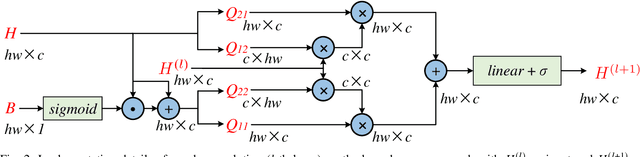
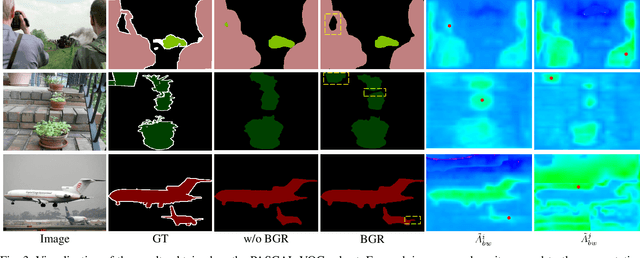
In this paper, we propose a Boundary-aware Graph Reasoning (BGR) module to learn long-range contextual features for semantic segmentation. Rather than directly construct the graph based on the backbone features, our BGR module explores a reasonable way to combine segmentation erroneous regions with the graph construction scenario. Motivated by the fact that most hard-to-segment pixels broadly distribute on boundary regions, our BGR module uses the boundary score map as prior knowledge to intensify the graph node connections and thereby guide the graph reasoning focus on boundary regions. In addition, we employ an efficient graph convolution implementation to reduce the computational cost, which benefits the integration of our BGR module into current segmentation backbones. Extensive experiments on three challenging segmentation benchmarks demonstrate the effectiveness of our proposed BGR module for semantic segmentation.

Fedlearn-Algo: A flexible open-source privacy-preserving machine learning platform

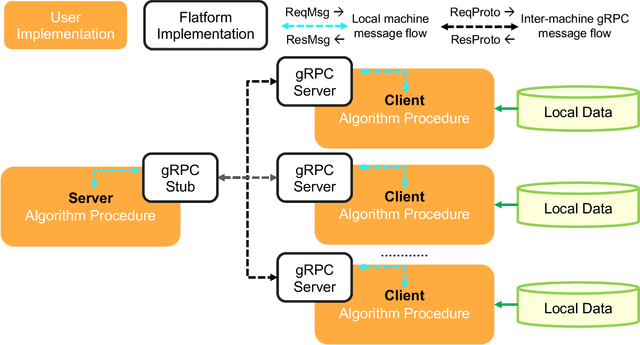
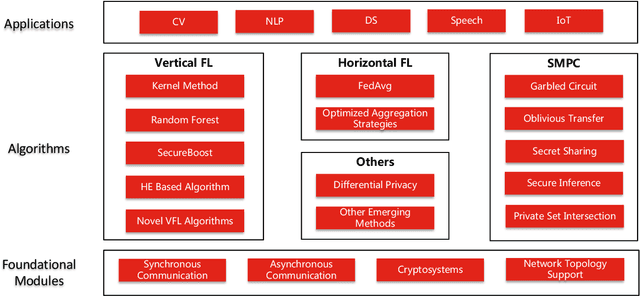
In this paper, we present Fedlearn-Algo, an open-source privacy preserving machine learning platform. We use this platform to demonstrate our research and development results on privacy preserving machine learning algorithms. As the first batch of novel FL algorithm examples, we release vertical federated kernel binary classification model and vertical federated random forest model. They have been tested to be more efficient than existing vertical federated learning models in our practice. Besides the novel FL algorithm examples, we also release a machine communication module. The uniform data transfer interface supports transferring widely used data formats between machines. We will maintain this platform by adding more functional modules and algorithm examples. The code is available at https://github.com/fedlearnAI/fedlearn-algo.

Enhanced Bilevel Optimization via Bregman Distance

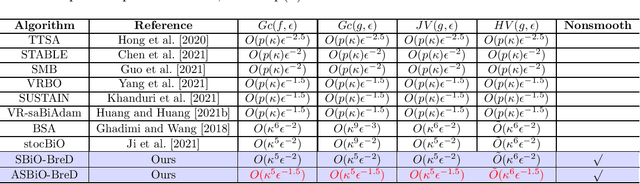
Bilevel optimization has been widely applied many machine learning problems such as hyperparameter optimization, policy optimization and meta learning. Although many bilevel optimization methods more recently have been proposed to solve the bilevel optimization problems, they still suffer from high computational complexities and do not consider the more general bilevel problems with nonsmooth regularization. In the paper, thus, we propose a class of efficient bilevel optimization methods based on Bregman distance. In our methods, we use the mirror decent iteration to solve the outer subproblem of the bilevel problem by using strongly-convex Bregman functions. Specifically, we propose a bilevel optimization method based on Bregman distance (BiO-BreD) for solving deterministic bilevel problems, which reaches the lower computational complexities than the best known results. We also propose a stochastic bilevel optimization method (SBiO-BreD) for solving stochastic bilevel problems based on the stochastic approximated gradients and Bregman distance. Further, we propose an accelerated version of SBiO-BreD method (ASBiO-BreD) by using the variance-reduced technique. Moreover, we prove that the ASBiO-BreD outperforms the best known computational complexities with respect to the condition number $\kappa$ and the target accuracy $\epsilon$ for finding an $\epsilon$-stationary point of nonconvex-strongly-convex bilevel problems. In particular, our methods can solve the bilevel optimization problems with nonsmooth regularization with a lower computational complexity.

AdaGDA: Faster Adaptive Gradient Descent Ascent Methods for Minimax Optimization

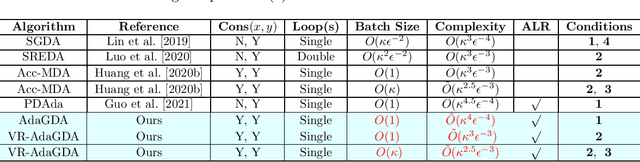
In the paper, we propose a class of faster adaptive gradient descent ascent methods for solving the nonconvex-strongly-concave minimax problems by using unified adaptive matrices used in the SUPER-ADAM \citep{huang2021super}. Specifically, we propose a fast adaptive gradient decent ascent (AdaGDA) method based on the basic momentum technique, which reaches a low sample complexity of $O(\kappa^4\epsilon^{-4})$ for finding an $\epsilon$-stationary point without large batches, which improves the existing result of adaptive minimax optimization method by a factor of $O(\sqrt{\kappa})$. Moreover, we present an accelerated version of AdaGDA (VR-AdaGDA) method based on the momentum-based variance reduced technique, which achieves the best known sample complexity of $O(\kappa^3\epsilon^{-3})$ for finding an $\epsilon$-stationary point without large batches. Further assume the bounded Lipschitz parameter of objective function, we prove that our VR-AdaGDA method reaches a lower sample complexity of $O(\kappa^{2.5}\epsilon^{-3})$ with the mini-batch size $O(\kappa)$. In particular, we provide an effective convergence analysis framework for our adaptive methods based on unified adaptive matrices, which include almost existing adaptive learning rates.