Obtaining Lower Query Complexities through Lightweight Zeroth-Order Proximal Gradient Algorithms

Zeroth-order (ZO) optimization is one key technique for machine learning problems where gradient calculation is expensive or impossible. Several variance reduced ZO proximal algorithms have been proposed to speed up ZO optimization for non-smooth problems, and all of them opted for the coordinated ZO estimator against the random ZO estimator when approximating the true gradient, since the former is more accurate. While the random ZO estimator introduces bigger error and makes convergence analysis more challenging compared to coordinated ZO estimator, it requires only $\mathcal{O}(1)$ computation, which is significantly less than $\mathcal{O}(d)$ computation of the coordinated ZO estimator, with $d$ being dimension of the problem space. To take advantage of the computationally efficient nature of the random ZO estimator, we first propose a ZO objective decrease (ZOOD) property which can incorporate two different types of errors in the upper bound of convergence rate. Next, we propose two generic reduction frameworks for ZO optimization which can automatically derive the convergence results for convex and non-convex problems respectively, as long as the convergence rate for the inner solver satisfies the ZOOD property. With the application of two reduction frameworks on our proposed ZOR-ProxSVRG and ZOR-ProxSAGA, two variance reduced ZO proximal algorithms with fully random ZO estimators, we improve the state-of-the-art function query complexities from $\mathcal{O}\left(\min\{\frac{dn^{1/2}}{\epsilon^2}, \frac{d}{\epsilon^3}\}\right)$ to $\tilde{\mathcal{O}}\left(\frac{n+d}{\epsilon^2}\right)$ under $d > n^{\frac{1}{2}}$ for non-convex problems, and from $\mathcal{O}\left(\frac{d}{\epsilon^2}\right)$ to $\tilde{\mathcal{O}}\left(n\log\frac{1}{\epsilon}+\frac{d}{\epsilon}\right)$ for convex problems.

FastCLIP: A Suite of Optimization Techniques to Accelerate CLIP Training with Limited Resources

Existing studies of training state-of-the-art Contrastive Language-Image Pretraining (CLIP) models on large-scale data involve hundreds of or even thousands of GPUs due to the requirement of a large batch size. However, such a large amount of resources is not accessible to most people. While advanced compositional optimization techniques for optimizing global contrastive losses have been demonstrated effective for removing the requirement of large batch size, their performance on large-scale data remains underexplored and not optimized. To bridge the gap, this paper explores several aspects of CLIP training with limited resources (e.g., up to tens of GPUs). First, we introduce FastCLIP, a general CLIP training framework built on advanced compositional optimization techniques while designed and optimized for the distributed setting. Our framework is equipped with an efficient gradient reduction strategy to reduce communication overhead. Second, to further boost training efficiency, we investigate three components of the framework from an optimization perspective: the schedule of the inner learning rate, the update rules of the temperature parameter and the model parameters, respectively. Experiments on different strategies for each component shed light on how to conduct CLIP training more efficiently. Finally, we benchmark the performance of FastCLIP and the state-of-the-art training baseline (OpenCLIP) on different compute scales up to 32 GPUs on 8 nodes, and three data scales ranging from 2.7 million, 9.1 million to 315 million image-text pairs to demonstrate the significant improvement of FastCLIP in the resource-limited setting. We release the code of FastCLIP at https://github.com/Optimization-AI/fast_clip .

Stability and Generalization of Stochastic Compositional Gradient Descent Algorithms

Many machine learning tasks can be formulated as a stochastic compositional optimization (SCO) problem such as reinforcement learning, AUC maximization, and meta-learning, where the objective function involves a nested composition associated with an expectation. While a significant amount of studies has been devoted to studying the convergence behavior of SCO algorithms, there is little work on understanding their generalization, i.e., how these learning algorithms built from training examples would behave on future test examples. In this paper, we provide the stability and generalization analysis of stochastic compositional gradient descent algorithms through the lens of algorithmic stability in the framework of statistical learning theory. Firstly, we introduce a stability concept called compositional uniform stability and establish its quantitative relation with generalization for SCO problems. Then, we establish the compositional uniform stability results for two popular stochastic compositional gradient descent algorithms, namely SCGD and SCSC. Finally, we derive dimension-independent excess risk bounds for SCGD and SCSC by trade-offing their stability results and optimization errors. To the best of our knowledge, these are the first-ever-known results on stability and generalization analysis of stochastic compositional gradient descent algorithms.

An Accelerated Variance-Reduced Conditional Gradient Sliding Algorithm for First-order and Zeroth-order Optimization

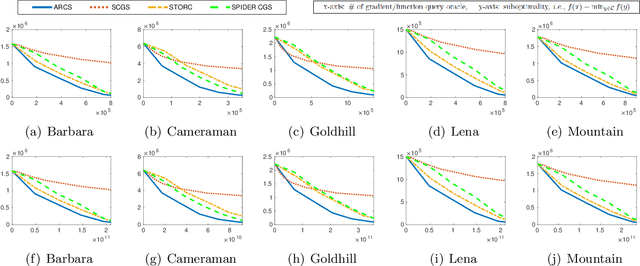
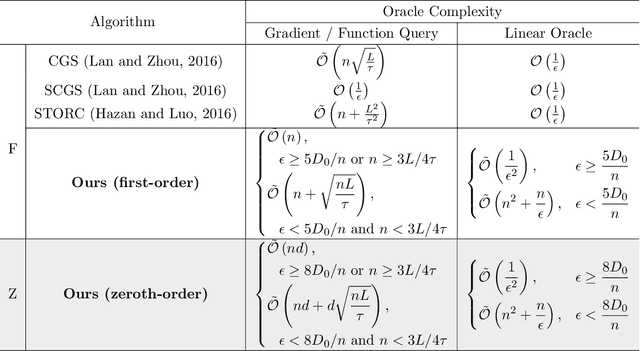
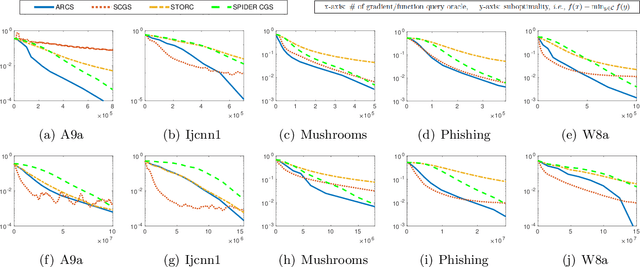
The conditional gradient algorithm (also known as the Frank-Wolfe algorithm) has recently regained popularity in the machine learning community due to its projection-free property to solve constrained problems. Although many variants of the conditional gradient algorithm have been proposed to improve performance, they depend on first-order information (gradient) to optimize. Naturally, these algorithms are unable to function properly in the field of increasingly popular zeroth-order optimization, where only zeroth-order information (function value) is available. To fill in this gap, we propose a novel Accelerated variance-Reduced Conditional gradient Sliding (ARCS) algorithm for finite-sum problems, which can use either first-order or zeroth-order information to optimize. To the best of our knowledge, ARCS is the first zeroth-order conditional gradient sliding type algorithms solving convex problems in zeroth-order optimization. In first-order optimization, the convergence results of ARCS substantially outperform previous algorithms in terms of the number of gradient query oracle. Finally we validated the superiority of ARCS by experiments on real-world datasets.