Efficiently Solving Turn-Taking Stochastic Games with Extensive-Form Correlation

We study equilibrium computation with extensive-form correlation in two-player turn-taking stochastic games. Our main results are two-fold: (1) We give an algorithm for computing a Stackelberg extensive-form correlated equilibrium (SEFCE), which runs in time polynomial in the size of the game, as well as the number of bits required to encode each input number. (2) We give an efficient algorithm for approximately computing an optimal extensive-form correlated equilibrium (EFCE) up to machine precision, i.e., the algorithm achieves approximation error $\varepsilon$ in time polynomial in the size of the game, as well as $\log(1 / \varepsilon)$. Our algorithm for SEFCE is the first polynomial-time algorithm for equilibrium computation with commitment in such a general class of stochastic games. Existing algorithms for SEFCE typically make stronger assumptions such as no chance moves, and are designed for extensive-form games in the less succinct tree form. Our algorithm for approximately optimal EFCE is, to our knowledge, the first algorithm that achieves 3 desiderata simultaneously: approximate optimality, polylogarithmic dependency on the approximation error, and compatibility with stochastic games in the more succinct graph form. Existing algorithms achieve at most 2 of these desiderata, often also relying on additional technical assumptions.

Strategic Littlestone Dimension: Improved Bounds on Online Strategic Classification

We study the problem of online binary classification in settings where strategic agents can modify their observable features to receive a positive classification. We model the set of feasible manipulations by a directed graph over the feature space, and assume the learner only observes the manipulated features instead of the original ones. We introduce the Strategic Littlestone Dimension, a new combinatorial measure that captures the joint complexity of the hypothesis class and the manipulation graph. We demonstrate that it characterizes the instance-optimal mistake bounds for deterministic learning algorithms in the realizable setting. We also achieve improved regret in the agnostic setting by a refined agnostic-to-realizable reduction that accounts for the additional challenge of not observing agents' original features. Finally, we relax the assumption that the learner knows the manipulation graph, instead assuming their knowledge is captured by a family of graphs. We derive regret bounds in both the realizable setting where all agents manipulate according to the same graph within the graph family, and the agnostic setting where the manipulation graphs are chosen adversarially and not consistently modeled by a single graph in the family.

Efficient Algorithms for Planning with Participation Constraints

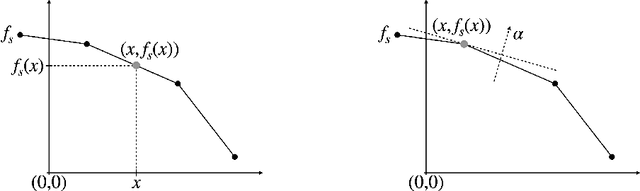
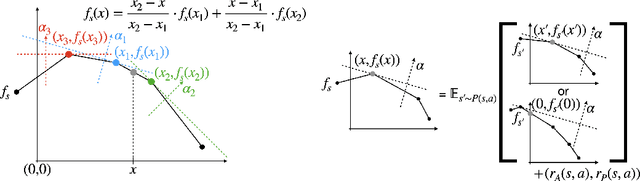
We consider the problem of planning with participation constraints introduced in [Zhang et al., 2022]. In this problem, a principal chooses actions in a Markov decision process, resulting in separate utilities for the principal and the agent. However, the agent can and will choose to end the process whenever his expected onward utility becomes negative. The principal seeks to compute and commit to a policy that maximizes her expected utility, under the constraint that the agent should always want to continue participating. We provide the first polynomial-time exact algorithm for this problem for finite-horizon settings, where previously only an additive $\varepsilon$-approximation algorithm was known. Our approach can also be extended to the (discounted) infinite-horizon case, for which we give an algorithm that runs in time polynomial in the size of the input and $\log(1/\varepsilon)$, and returns a policy that is optimal up to an additive error of $\varepsilon$.

Near-Optimal Reviewer Splitting in Two-Phase Paper Reviewing and Conference Experiment Design

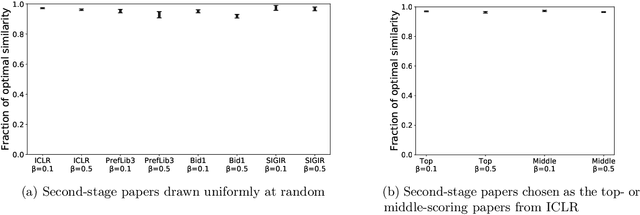
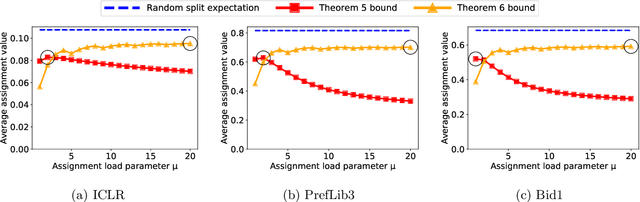
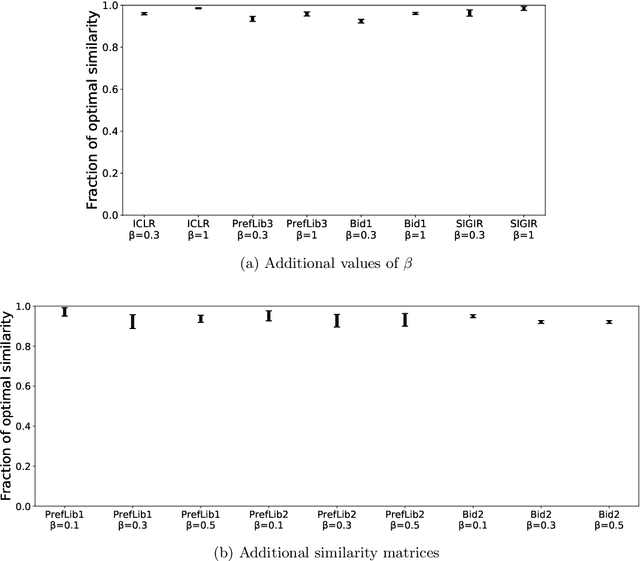
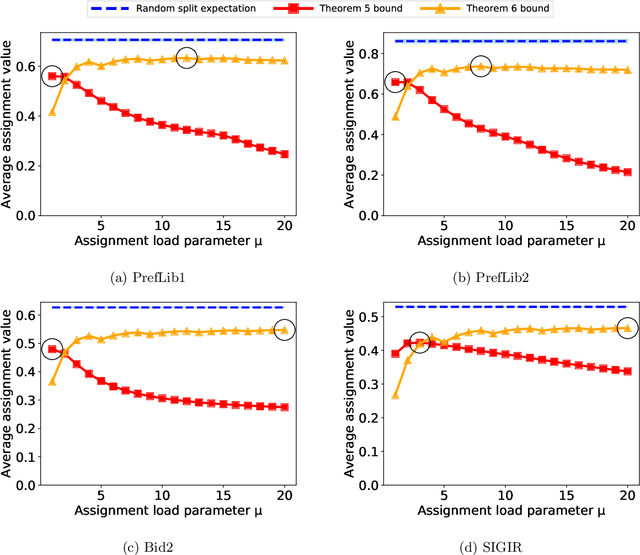
Many scientific conferences employ a two-phase paper review process, where some papers are assigned additional reviewers after the initial reviews are submitted. Many conferences also design and run experiments on their paper review process, where some papers are assigned reviewers who provide reviews under an experimental condition. In this paper, we consider the question: how should reviewers be divided between phases or conditions in order to maximize total assignment similarity? We make several contributions towards answering this question. First, we prove that when the set of papers requiring additional review is unknown, a simplified variant of this problem is NP-hard. Second, we empirically show that across several datasets pertaining to real conference data, dividing reviewers between phases/conditions uniformly at random allows an assignment that is nearly as good as the oracle optimal assignment. This uniformly random choice is practical for both the two-phase and conference experiment design settings. Third, we provide explanations of this phenomenon by providing theoretical bounds on the suboptimality of this random strategy under certain natural conditions. From these easily-interpretable conditions, we provide actionable insights to conference program chairs about whether a random reviewer split is suitable for their conference.

Automated Mechanism Design for Classification with Partial Verification

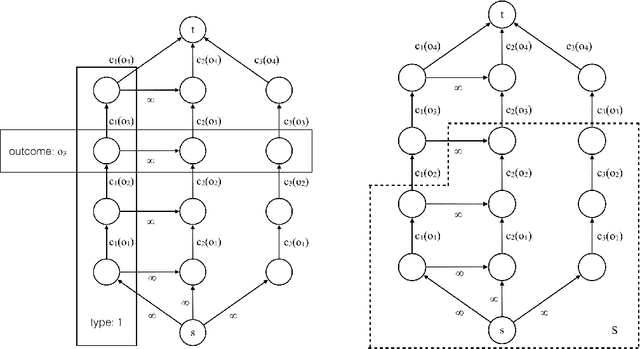
We study the problem of automated mechanism design with partial verification, where each type can (mis)report only a restricted set of types (rather than any other type), induced by the principal's limited verification power. We prove hardness results when the revelation principle does not necessarily hold, as well as when types have even minimally different preferences. In light of these hardness results, we focus on truthful mechanisms in the setting where all types share the same preference over outcomes, which is motivated by applications in, e.g., strategic classification. We present a number of algorithmic and structural results, including an efficient algorithm for finding optimal deterministic truthful mechanisms, which also implies a faster algorithm for finding optimal randomized truthful mechanisms via a characterization based on convexity. We then consider a more general setting, where the principal's cost is a function of the combination of outcomes assigned to each type. In particular, we focus on the case where the cost function is submodular, and give generalizations of essentially all our results in the classical setting where the cost function is additive. Our results provide a relatively complete picture for automated mechanism design with partial verification.

Classification with Strategically Withheld Data

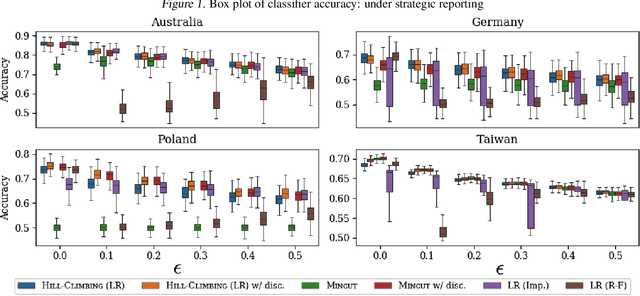
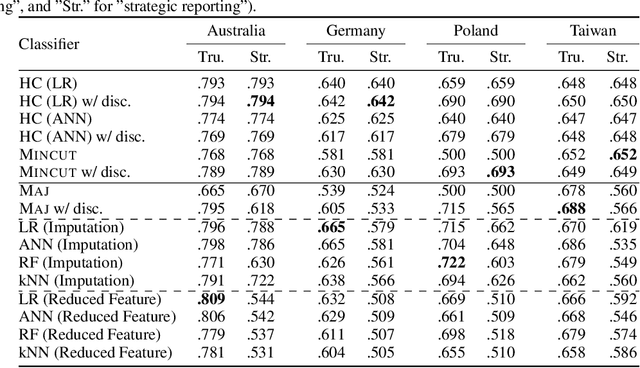
Machine learning techniques can be useful in applications such as credit approval and college admission. However, to be classified more favorably in such contexts, an agent may decide to strategically withhold some of her features, such as bad test scores. This is a missing data problem with a twist: which data is missing {\em depends on the chosen classifier}, because the specific classifier is what may create the incentive to withhold certain feature values. We address the problem of training classifiers that are robust to this behavior. We design three classification methods: {\sc Mincut}, {\sc Hill-Climbing} ({\sc HC}) and Incentive-Compatible Logistic Regression ({\sc IC-LR}). We show that {\sc Mincut} is optimal when the true distribution of data is fully known. However, it can produce complex decision boundaries, and hence be prone to overfitting in some cases. Based on a characterization of truthful classifiers (i.e., those that give no incentive to strategically hide features), we devise a simpler alternative called {\sc HC} which consists of a hierarchical ensemble of out-of-the-box classifiers, trained using a specialized hill-climbing procedure which we show to be convergent. For several reasons, {\sc Mincut} and {\sc HC} are not effective in utilizing a large number of complementarily informative features. To this end, we present {\sc IC-LR}, a modification of Logistic Regression that removes the incentive to strategically drop features. We also show that our algorithms perform well in experiments on real-world data sets, and present insights into their relative performance in different settings.

Planning with Submodular Objective Functions

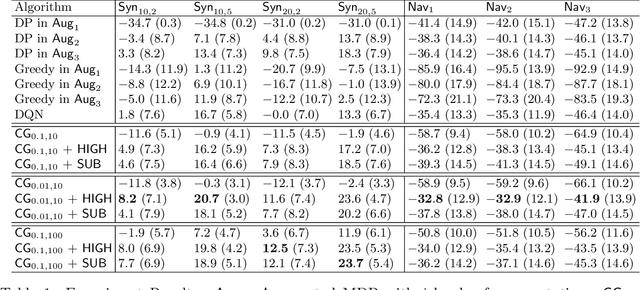
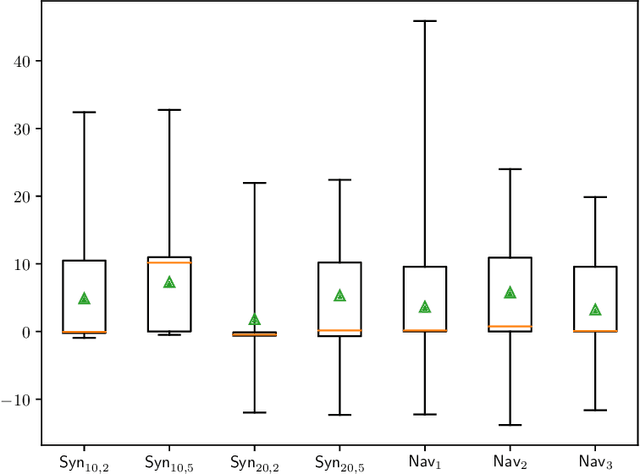
We study planning with submodular objective functions, where instead of maximizing the cumulative reward, the goal is to maximize the objective value induced by a submodular function. Our framework subsumes standard planning and submodular maximization with cardinality constraints as special cases, and thus many practical applications can be naturally formulated within our framework. Based on the notion of multilinear extension, we propose a novel and theoretically principled algorithmic framework for planning with submodular objective functions, which recovers classical algorithms when applied to the two special cases mentioned above. Empirically, our approach significantly outperforms baseline algorithms on synthetic environments and navigation tasks.

Mitigating Manipulation in Peer Review via Randomized Reviewer Assignments

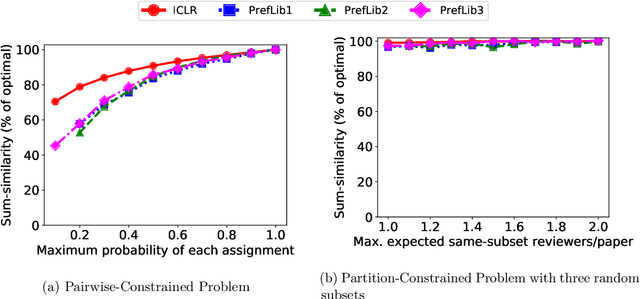
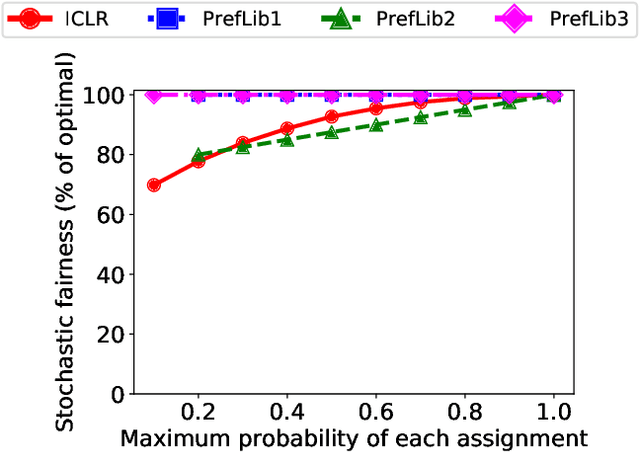
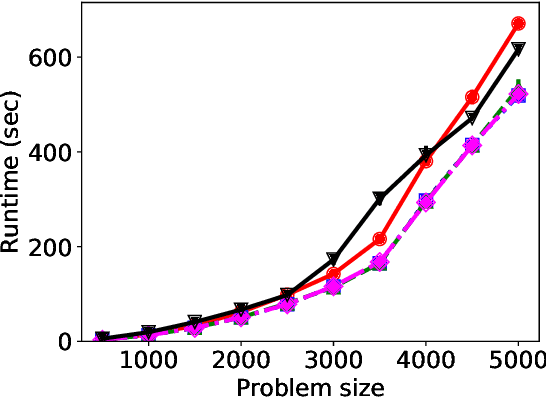
We consider three important challenges in conference peer review: (i) reviewers maliciously attempting to get assigned to certain papers to provide positive reviews, possibly as part of quid-pro-quo arrangements with the authors; (ii) "torpedo reviewing," where reviewers deliberately attempt to get assigned to certain papers that they dislike in order to reject them; (iii) reviewer de-anonymization on release of the similarities and the reviewer-assignment code. On the conceptual front, we identify connections between these three problems and present a framework that brings all these challenges under a common umbrella. We then present a (randomized) algorithm for reviewer assignment that can optimally solve the reviewer-assignment problem under any given constraints on the probability of assignment for any reviewer-paper pair. We further consider the problem of restricting the joint probability that certain suspect pairs of reviewers are assigned to certain papers, and show that this problem is NP-hard for arbitrary constraints on these joint probabilities but efficiently solvable for a practical special case. Finally, we experimentally evaluate our algorithms on datasets from past conferences, where we observe that they can limit the chance that any malicious reviewer gets assigned to their desired paper to 50% while producing assignments with over 90% of the total optimal similarity. Our algorithms still achieve this similarity while also preventing reviewers with close associations from being assigned to the same paper.

Nearly Linear Row Sampling Algorithm for Quantile Regression

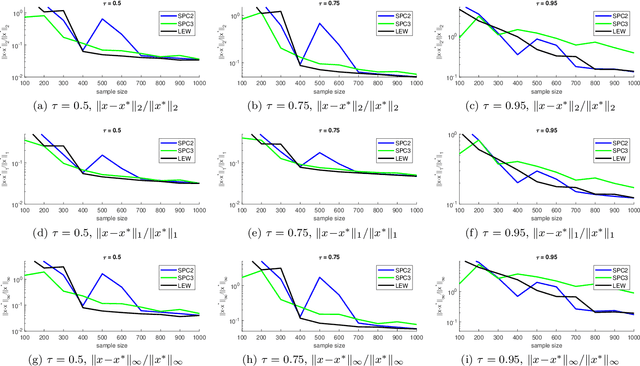
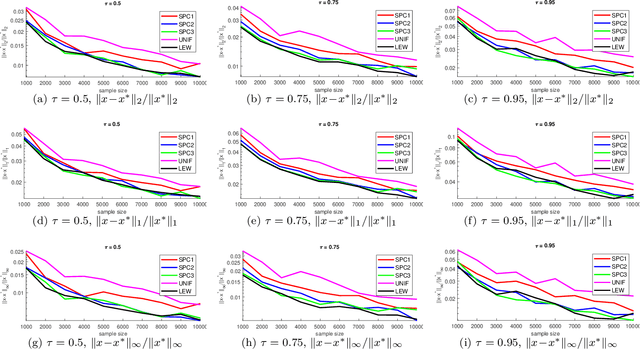
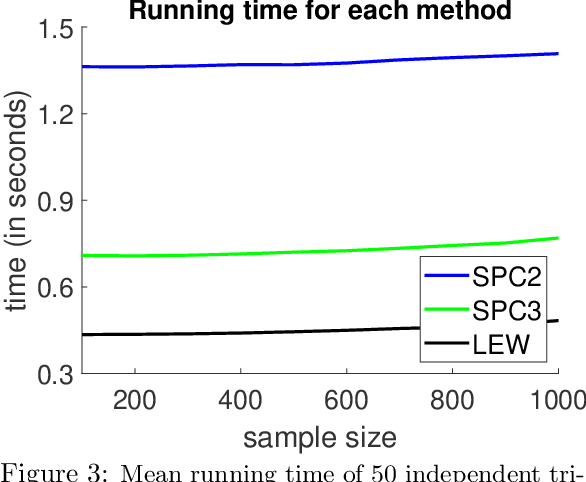
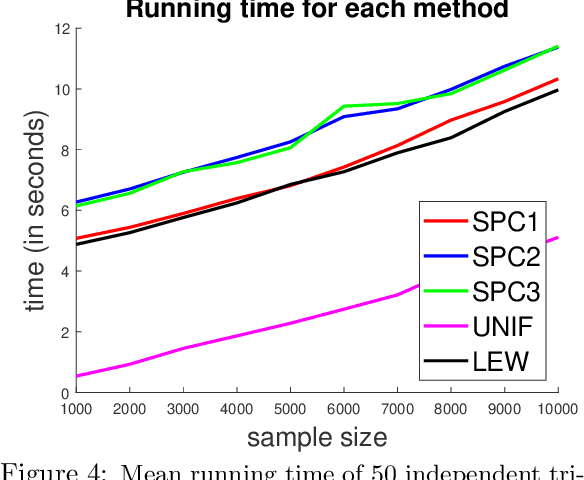
We give a row sampling algorithm for the quantile loss function with sample complexity nearly linear in the dimensionality of the data, improving upon the previous best algorithm whose sampling complexity has at least cubic dependence on the dimensionality. Based upon our row sampling algorithm, we give the fastest known algorithm for quantile regression and a graph sparsification algorithm for balanced directed graphs. Our main technical contribution is to show that Lewis weights sampling, which has been used in row sampling algorithms for $\ell_p$ norms, can also be applied in row sampling algorithms for a variety of loss functions. We complement our theoretical results by experiments to demonstrate the practicality of our approach.

Provably Efficient $Q$-learning with Function Approximation via Distribution Shift Error Checking Oracle

$Q$-learning with function approximation is one of the most popular methods in reinforcement learning. Though the idea of using function approximation was proposed at least $60$ years ago, even in the simplest setup, i.e, approximating $Q$-functions with linear functions, it is still an open problem how to design a provably efficient algorithm that learns a near-optimal policy. The key challenges are how to efficiently explore the state space and how to decide when to stop exploring in conjunction with the function approximation scheme. The current paper presents a provably efficient algorithm for $Q$-learning with linear function approximation. Under certain regularity assumptions, our algorithm, Difference Maximization $Q$-learning (DMQ), combined with linear function approximation, returns a near optimal policy using polynomial number of trajectories. Our algorithm introduces a new notion, the Distribution Shift Error Checking (DSEC) oracle. This oracle tests whether there exists a function in the function class that predicts well on a distribution $\mathcal{D}_1$, but predicts poorly on another distribution $\mathcal{D}_2$, where $\mathcal{D}_1$ and $\mathcal{D}_2$ are distributions over states induced by two different exploration policies. For the linear function class, this oracle is equivalent to solving a top eigenvalue problem. We believe our algorithmic insights, especially the DSEC oracle, are also useful in designing and analyzing reinforcement learning algorithms with general function approximation.