Replicable Online Learning

We investigate the concept of algorithmic replicability introduced by Impagliazzo et al. 2022, Ghazi et al. 2021, Ahn et al. 2024 in an online setting. In our model, the input sequence received by the online learner is generated from time-varying distributions chosen by an adversary (obliviously). Our objective is to design low-regret online algorithms that, with high probability, produce the exact same sequence of actions when run on two independently sampled input sequences generated as described above. We refer to such algorithms as adversarially replicable. Previous works (such as Esfandiari et al. 2022) explored replicability in the online setting under inputs generated independently from a fixed distribution; we term this notion as iid-replicability. Our model generalizes to capture both adversarial and iid input sequences, as well as their mixtures, which can be modeled by setting certain distributions as point-masses. We demonstrate adversarially replicable online learning algorithms for online linear optimization and the experts problem that achieve sub-linear regret. Additionally, we propose a general framework for converting an online learner into an adversarially replicable one within our setting, bounding the new regret in terms of the original algorithm's regret. We also present a nearly optimal (in terms of regret) iid-replicable online algorithm for the experts problem, highlighting the distinction between the iid and adversarial notions of replicability. Finally, we establish lower bounds on the regret (in terms of the replicability parameter and time) that any replicable online algorithm must incur.

VisMin: Visual Minimal-Change Understanding

Fine-grained understanding of objects, attributes, and relationships between objects is crucial for visual-language models (VLMs). Existing benchmarks primarily focus on evaluating VLMs' capability to distinguish between two very similar \textit{captions} given an image. In this paper, we introduce a new, challenging benchmark termed \textbf{Vis}ual \textbf{Min}imal-Change Understanding (VisMin), which requires models to predict the correct image-caption match given two images and two captions. The image pair and caption pair contain minimal changes, i.e., only one aspect changes at a time from among the following: \textit{object}, \textit{attribute}, \textit{count}, and \textit{spatial relation}. These changes test the models' understanding of objects, attributes (such as color, material, shape), counts, and spatial relationships between objects. We built an automatic framework using large language models and diffusion models, followed by a rigorous 4-step verification process by human annotators. Empirical experiments reveal that current VLMs exhibit notable deficiencies in understanding spatial relationships and counting abilities. We also generate a large-scale training dataset to finetune CLIP and Idefics2, showing significant improvements in fine-grained understanding across benchmarks and in CLIP's general image-text alignment. We release all resources, including the benchmark, training data, and finetuned model checkpoints, at \url{https://vismin.net/}.

Strategic Littlestone Dimension: Improved Bounds on Online Strategic Classification

We study the problem of online binary classification in settings where strategic agents can modify their observable features to receive a positive classification. We model the set of feasible manipulations by a directed graph over the feature space, and assume the learner only observes the manipulated features instead of the original ones. We introduce the Strategic Littlestone Dimension, a new combinatorial measure that captures the joint complexity of the hypothesis class and the manipulation graph. We demonstrate that it characterizes the instance-optimal mistake bounds for deterministic learning algorithms in the realizable setting. We also achieve improved regret in the agnostic setting by a refined agnostic-to-realizable reduction that accounts for the additional challenge of not observing agents' original features. Finally, we relax the assumption that the learner knows the manipulation graph, instead assuming their knowledge is captured by a family of graphs. We derive regret bounds in both the realizable setting where all agents manipulate according to the same graph within the graph family, and the agnostic setting where the manipulation graphs are chosen adversarially and not consistently modeled by a single graph in the family.

Distributional Adversarial Loss

A major challenge in defending against adversarial attacks is the enormous space of possible attacks that even a simple adversary might perform. To address this, prior work has proposed a variety of defenses that effectively reduce the size of this space. These include randomized smoothing methods that add noise to the input to take away some of the adversary's impact. Another approach is input discretization which limits the adversary's possible number of actions. Motivated by these two approaches, we introduce a new notion of adversarial loss which we call distributional adversarial loss, to unify these two forms of effectively weakening an adversary. In this notion, we assume for each original example, the allowed adversarial perturbation set is a family of distributions (e.g., induced by a smoothing procedure), and the adversarial loss over each example is the maximum loss over all the associated distributions. The goal is to minimize the overall adversarial loss. We show generalization guarantees for our notion of adversarial loss in terms of the VC-dimension of the hypothesis class and the size of the set of allowed adversarial distributions associated with each input. We also investigate the role of randomness in achieving robustness against adversarial attacks in the methods described above. We show a general derandomization technique that preserves the extent of a randomized classifier's robustness against adversarial attacks. We corroborate the procedure experimentally via derandomizing the Random Projection Filters framework of \cite{dong2023adversarial}. Our procedure also improves the robustness of the model against various adversarial attacks.

An Examination of the Robustness of Reference-Free Image Captioning Evaluation Metrics

Recently, reference-free metrics such as CLIPScore (Hessel et al., 2021) and UMIC (Lee et al., 2021) have been proposed for automatic evaluation of image captions, demonstrating a high correlation with human judgment. In this work, our focus lies in evaluating the robustness of these metrics in scenarios that require distinguishing between two captions with high lexical overlap but very different meanings. Our findings reveal that despite their high correlation with human judgment, both CLIPScore and UMIC struggle to identify fine-grained errors in captions. However, when comparing different types of fine-grained errors, both metrics exhibit limited sensitivity to implausibility of captions and strong sensitivity to lack of sufficient visual grounding. Probing further into the visual grounding aspect, we found that both CLIPScore and UMIC are impacted by the size of image-relevant objects mentioned in the caption, and that CLIPScore is also sensitive to the number of mentions of image-relevant objects in the caption. In terms of linguistic aspects of a caption, we found that both metrics lack the ability to comprehend negation, UMIC is sensitive to caption lengths, and CLIPScore is insensitive to the structure of the sentence. We hope our findings will serve as a valuable guide towards improving reference-free evaluation in image captioning.

Certifiable (Multi)Robustness Against Patch Attacks Using ERM

Consider patch attacks, where at test-time an adversary manipulates a test image with a patch in order to induce a targeted misclassification. We consider a recent defense to patch attacks, Patch-Cleanser (Xiang et al. [2022]). The Patch-Cleanser algorithm requires a prediction model to have a ``two-mask correctness'' property, meaning that the prediction model should correctly classify any image when any two blank masks replace portions of the image. Xiang et al. learn a prediction model to be robust to two-mask operations by augmenting the training set with pairs of masks at random locations of training images and performing empirical risk minimization (ERM) on the augmented dataset. However, in the non-realizable setting when no predictor is perfectly correct on all two-mask operations on all images, we exhibit an example where ERM fails. To overcome this challenge, we propose a different algorithm that provably learns a predictor robust to all two-mask operations using an ERM oracle, based on prior work by Feige et al. [2015]. We also extend this result to a multiple-group setting, where we can learn a predictor that achieves low robust loss on all groups simultaneously.

Fundamental Bounds on Online Strategic Classification

We study the problem of online binary classification where strategic agents can manipulate their observable features in predefined ways, modeled by a manipulation graph, in order to receive a positive classification. We show this setting differs in fundamental ways from non-strategic online classification. For instance, whereas in the non-strategic case, a mistake bound of $\ln|H|$ is achievable via the halving algorithm when the target function belongs to a known class $H$, we show that no deterministic algorithm can achieve a mistake bound $o(\Delta)$ in the strategic setting, where $\Delta$ is the maximum degree of the manipulation graph (even when $|H|=O(\Delta)$). We obtain an algorithm achieving mistake bound $O(\Delta\ln|H|)$. We also extend this to the agnostic setting and obtain an algorithm with a $\Delta$ multiplicative regret, and we show no deterministic algorithm can achieve $o(\Delta)$ multiplicative regret. Next, we study two randomized models based on whether the random choices are made before or after agents respond, and show they exhibit fundamental differences. In the first model, at each round the learner deterministically chooses a probability distribution over classifiers inducing expected values on each vertex (probabilities of being classified as positive), which the strategic agents respond to. We show that any learner in this model has to suffer linear regret. On the other hand, in the second model, while the adversary who selects the next agent must respond to the learner's probability distribution over classifiers, the agent then responds to the actual hypothesis classifier drawn from this distribution. Surprisingly, we show this model is more advantageous to the learner, and we design randomized algorithms that achieve sublinear regret bounds against both oblivious and adaptive adversaries.

MAPL: Parameter-Efficient Adaptation of Unimodal Pre-Trained Models for Vision-Language Few-Shot Prompting

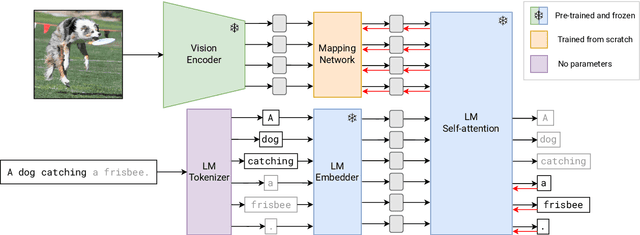
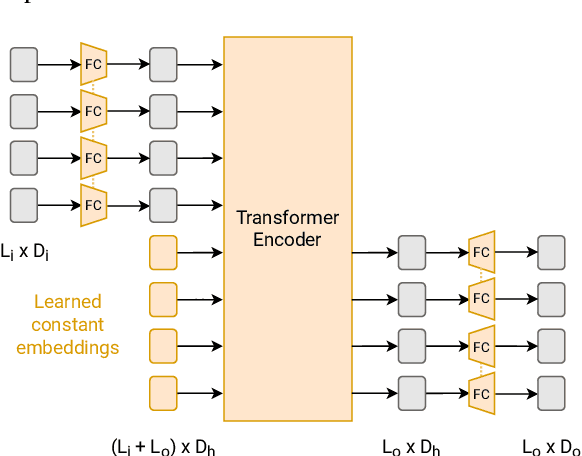
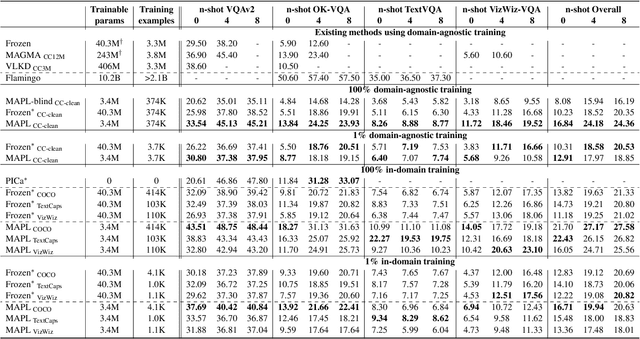
Large pre-trained models have proved to be remarkable zero- and (prompt-based) few-shot learners in unimodal vision and language tasks. We propose MAPL, a simple and parameter-efficient method that reuses frozen pre-trained unimodal models and leverages their strong generalization capabilities in multimodal vision-language (VL) settings. MAPL learns a lightweight mapping between the representation spaces of unimodal models using aligned image-text data, and can generalize to unseen VL tasks from just a few in-context examples. The small number of trainable parameters makes MAPL effective at low-data and in-domain learning. Moreover, MAPL's modularity enables easy extension to other pre-trained models. Extensive experiments on several visual question answering and image captioning benchmarks show that MAPL achieves superior or competitive performance compared to similar methods while training orders of magnitude fewer parameters. MAPL can be trained in just a few hours using modest computational resources and public datasets. We plan to release the code and pre-trained models.

Individual Preference Stability for Clustering

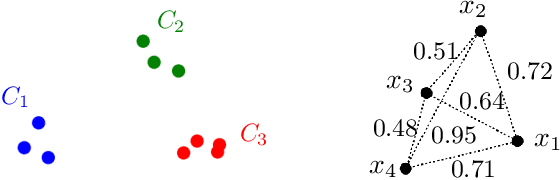
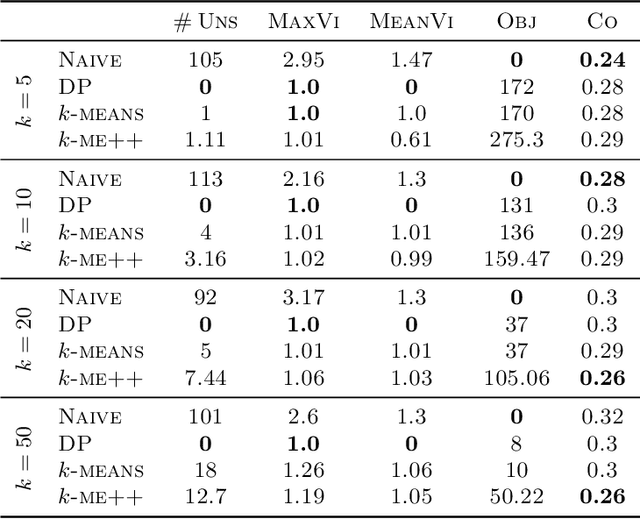
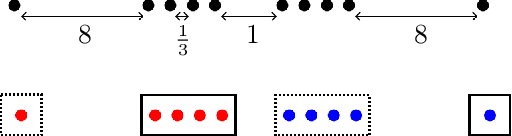
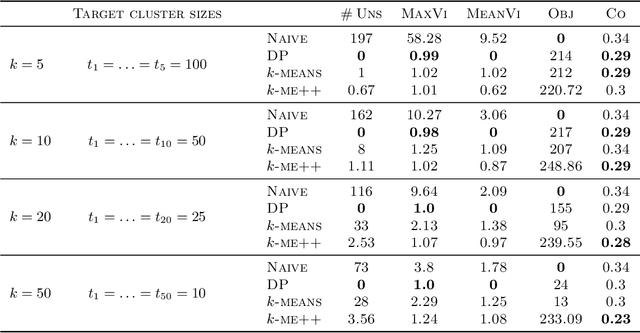
In this paper, we propose a natural notion of individual preference (IP) stability for clustering, which asks that every data point, on average, is closer to the points in its own cluster than to the points in any other cluster. Our notion can be motivated from several perspectives, including game theory and algorithmic fairness. We study several questions related to our proposed notion. We first show that deciding whether a given data set allows for an IP-stable clustering in general is NP-hard. As a result, we explore the design of efficient algorithms for finding IP-stable clusterings in some restricted metric spaces. We present a polytime algorithm to find a clustering satisfying exact IP-stability on the real line, and an efficient algorithm to find an IP-stable 2-clustering for a tree metric. We also consider relaxing the stability constraint, i.e., every data point should not be too far from its own cluster compared to any other cluster. For this case, we provide polytime algorithms with different guarantees. We evaluate some of our algorithms and several standard clustering approaches on real data sets.

Setting Fair Incentives to Maximize Improvement

We consider the problem of helping agents improve by setting short-term goals. Given a set of target skill levels, we assume each agent will try to improve from their initial skill level to the closest target level within reach or do nothing if no target level is within reach. We consider two models: the common improvement capacity model, where agents have the same limit on how much they can improve, and the individualized improvement capacity model, where agents have individualized limits. Our goal is to optimize the target levels for social welfare and fairness objectives, where social welfare is defined as the total amount of improvement, and fairness objectives are considered where the agents belong to different underlying populations. A key technical challenge of this problem is the non-monotonicity of social welfare in the set of target levels, i.e., adding a new target level may decrease the total amount of improvement as it may get easier for some agents to improve. This is especially challenging when considering multiple groups because optimizing target levels in isolation for each group and outputting the union may result in arbitrarily low improvement for a group, failing the fairness objective. Considering these properties, we provide algorithms for optimal and near-optimal improvement for both social welfare and fairness objectives. These algorithmic results work for both the common and individualized improvement capacity models. Furthermore, we show a placement of target levels exists that is approximately optimal for the social welfare of each group. Unlike the algorithmic results, this structural statement only holds in the common improvement capacity model, and we show counterexamples in the individualized improvement capacity model. Finally, we extend our algorithms to learning settings where we have only sample access to the initial skill levels of agents.