AccidentBench: Benchmarking Multimodal Understanding and Reasoning in Vehicle Accidents and Beyond

Rapid advances in multimodal models demand benchmarks that rigorously evaluate understanding and reasoning in safety-critical, dynamic real-world settings. We present AccidentBench, a large-scale benchmark that combines vehicle accident scenarios with Beyond domains, safety-critical settings in air and water that emphasize spatial and temporal reasoning (e.g., navigation, orientation, multi-vehicle motion). The benchmark contains approximately 2000 videos and over 19000 human-annotated question--answer pairs spanning multiple video lengths (short/medium/long) and difficulty levels (easy/medium/hard). Tasks systematically probe core capabilities: temporal, spatial, and intent understanding and reasoning. By unifying accident-centric traffic scenes with broader safety-critical scenarios in air and water, AccidentBench offers a comprehensive, physically grounded testbed for evaluating models under real-world variability. Evaluations of state-of-the-art models (e.g., Gemini-2.5 Pro and GPT-5) show that even the strongest models achieve only about 18% accuracy on the hardest tasks and longest videos, revealing substantial gaps in real-world temporal, spatial, and intent reasoning. AccidentBench is designed to expose these critical gaps and drive the development of multimodal models that are safer, more robust, and better aligned with real-world safety-critical challenges. The code and dataset are available at: https://github.com/SafeRL-Lab/AccidentBench

Towards VM Rescheduling Optimization Through Deep Reinforcement Learning

Modern industry-scale data centers need to manage a large number of virtual machines (VMs). Due to the continual creation and release of VMs, many small resource fragments are scattered across physical machines (PMs). To handle these fragments, data centers periodically reschedule some VMs to alternative PMs, a practice commonly referred to as VM rescheduling. Despite the increasing importance of VM rescheduling as data centers grow in size, the problem remains understudied. We first show that, unlike most combinatorial optimization tasks, the inference time of VM rescheduling algorithms significantly influences their performance, due to dynamic VM state changes during this period. This causes existing methods to scale poorly. Therefore, we develop a reinforcement learning system for VM rescheduling, VM2RL, which incorporates a set of customized techniques, such as a two-stage framework that accommodates diverse constraints and workload conditions, a feature extraction module that captures relational information specific to rescheduling, as well as a risk-seeking evaluation enabling users to optimize the trade-off between latency and accuracy. We conduct extensive experiments with data from an industry-scale data center. Our results show that VM2RL can achieve a performance comparable to the optimal solution but with a running time of seconds. Code and datasets are open-sourced: https://github.com/zhykoties/VMR2L_eurosys, https://drive.google.com/drive/folders/1PfRo1cVwuhH30XhsE2Np3xqJn2GpX5qy.

Few-Shot Test-Time Optimization Without Retraining for Semiconductor Recipe Generation and Beyond

We introduce Model Feedback Learning (MFL), a novel test-time optimization framework for optimizing inputs to pre-trained AI models or deployed hardware systems without requiring any retraining of the models or modifications to the hardware. In contrast to existing methods that rely on adjusting model parameters, MFL leverages a lightweight reverse model to iteratively search for optimal inputs, enabling efficient adaptation to new objectives under deployment constraints. This framework is particularly advantageous in real-world settings, such as semiconductor manufacturing recipe generation, where modifying deployed systems is often infeasible or cost-prohibitive. We validate MFL on semiconductor plasma etching tasks, where it achieves target recipe generation in just five iterations, significantly outperforming both Bayesian optimization and human experts. Beyond semiconductor applications, MFL also demonstrates strong performance in chemical processes (e.g., chemical vapor deposition) and electronic systems (e.g., wire bonding), highlighting its broad applicability. Additionally, MFL incorporates stability-aware optimization, enhancing robustness to process variations and surpassing conventional supervised learning and random search methods in high-dimensional control settings. By enabling few-shot adaptation, MFL provides a scalable and efficient paradigm for deploying intelligent control in real-world environments.

Reward-Safety Balance in Offline Safe RL via Diffusion Regularization

Constrained reinforcement learning (RL) seeks high-performance policies under safety constraints. We focus on an offline setting where the agent has only a fixed dataset -- common in realistic tasks to prevent unsafe exploration. To address this, we propose Diffusion-Regularized Constrained Offline Reinforcement Learning (DRCORL), which first uses a diffusion model to capture the behavioral policy from offline data and then extracts a simplified policy to enable efficient inference. We further apply gradient manipulation for safety adaptation, balancing the reward objective and constraint satisfaction. This approach leverages high-quality offline data while incorporating safety requirements. Empirical results show that DRCORL achieves reliable safety performance, fast inference, and strong reward outcomes across robot learning tasks. Compared to existing safe offline RL methods, it consistently meets cost limits and performs well with the same hyperparameters, indicating practical applicability in real-world scenarios.

Bagging Improves Generalization Exponentially

Bagging is a popular ensemble technique to improve the accuracy of machine learning models. It hinges on the well-established rationale that, by repeatedly retraining on resampled data, the aggregated model exhibits lower variance and hence higher stability, especially for discontinuous base learners. In this paper, we provide a new perspective on bagging: By suitably aggregating the base learners at the parametrization instead of the output level, bagging improves generalization performances exponentially, a strength that is significantly more powerful than variance reduction. More precisely, we show that for general stochastic optimization problems that suffer from slowly (i.e., polynomially) decaying generalization errors, bagging can effectively reduce these errors to an exponential decay. Moreover, this power of bagging is agnostic to the solution schemes, including common empirical risk minimization, distributionally robust optimization, and various regularizations. We demonstrate how bagging can substantially improve generalization performances in a range of examples involving heavy-tailed data that suffer from intrinsically slow rates.

Scalable Primal-Dual Actor-Critic Method for Safe Multi-Agent RL with General Utilities

We investigate safe multi-agent reinforcement learning, where agents seek to collectively maximize an aggregate sum of local objectives while satisfying their own safety constraints. The objective and constraints are described by {\it general utilities}, i.e., nonlinear functions of the long-term state-action occupancy measure, which encompass broader decision-making goals such as risk, exploration, or imitations. The exponential growth of the state-action space size with the number of agents presents challenges for global observability, further exacerbated by the global coupling arising from agents' safety constraints. To tackle this issue, we propose a primal-dual method utilizing shadow reward and $\kappa$-hop neighbor truncation under a form of correlation decay property, where $\kappa$ is the communication radius. In the exact setting, our algorithm converges to a first-order stationary point (FOSP) at the rate of $\mathcal{O}\left(T^{-2/3}\right)$. In the sample-based setting, we demonstrate that, with high probability, our algorithm requires $\widetilde{\mathcal{O}}\left(\epsilon^{-3.5}\right)$ samples to achieve an $\epsilon$-FOSP with an approximation error of $\mathcal{O}(\phi_0^{2\kappa})$, where $\phi_0\in (0,1)$. Finally, we demonstrate the effectiveness of our model through extensive numerical experiments.

Scalable Multi-Agent Reinforcement Learning with General Utilities

We study the scalable multi-agent reinforcement learning (MARL) with general utilities, defined as nonlinear functions of the team's long-term state-action occupancy measure. The objective is to find a localized policy that maximizes the average of the team's local utility functions without the full observability of each agent in the team. By exploiting the spatial correlation decay property of the network structure, we propose a scalable distributed policy gradient algorithm with shadow reward and localized policy that consists of three steps: (1) shadow reward estimation, (2) truncated shadow Q-function estimation, and (3) truncated policy gradient estimation and policy update. Our algorithm converges, with high probability, to $\epsilon$-stationarity with $\widetilde{\mc{O}}(\epsilon^{-2})$ samples up to some approximation error that decreases exponentially in the communication radius. This is the first result in the literature on multi-agent RL with general utilities that does not require the full observability.

Policy-based Primal-Dual Methods for Convex Constrained Markov Decision Processes

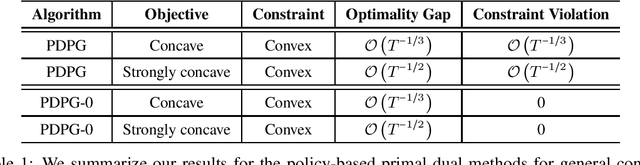
We study convex Constrained Markov Decision Processes (CMDPs) in which the objective is concave and the constraints are convex in the state-action visitation distribution. We propose a policy-based primal-dual algorithm that updates the primal variable via policy gradient ascent and updates the dual variable via projected sub-gradient descent. Despite the loss of additivity structure and the nonconvex nature, we establish the global convergence of the proposed algorithm by leveraging a hidden convexity in the problem under the general soft-max parameterization, and prove the $\mathcal{O}\left(T^{-1/3}\right)$ convergence rate in terms of both optimality gap and constraint violation. When the objective is strongly concave in the visitation distribution, we prove an improved convergence rate of $\mathcal{O}\left(T^{-1/2}\right)$. By introducing a pessimistic term to the constraint, we further show that a zero constraint violation can be achieved while preserving the same convergence rate for the optimality gap. This work is the first one in the literature that establishes non-asymptotic convergence guarantees for policy-based primal-dual methods for solving infinite-horizon discounted convex CMDPs.

A Dual Approach to Constrained Markov Decision Processes with Entropy Regularization

We study entropy-regularized constrained Markov decision processes (CMDPs) under the soft-max parameterization, in which an agent aims to maximize the entropy-regularized value function while satisfying constraints on the expected total utility. By leveraging the entropy regularization, our theoretical analysis shows that its Lagrangian dual function is smooth and the Lagrangian duality gap can be decomposed into the primal optimality gap and the constraint violation. Furthermore, we propose an accelerated dual-descent method for entropy-regularized CMDPs. We prove that our method achieves the global convergence rate $\widetilde{\mathcal{O}}(1/T)$ for both the optimality gap and the constraint violation for entropy-regularized CMDPs. A discussion about a linear convergence rate for CMDPs with a single constraint is also provided.