Corgi^2: A Hybrid Offline-Online Approach To Storage-Aware Data Shuffling For SGD

When using Stochastic Gradient Descent (SGD) for training machine learning models, it is often crucial to provide the model with examples sampled at random from the dataset. However, for large datasets stored in the cloud, random access to individual examples is often costly and inefficient. A recent work \cite{corgi}, proposed an online shuffling algorithm called CorgiPile, which greatly improves efficiency of data access, at the cost some performance loss, which is particularly apparent for large datasets stored in homogeneous shards (e.g., video datasets). In this paper, we introduce a novel two-step partial data shuffling strategy for SGD which combines an offline iteration of the CorgiPile method with a subsequent online iteration. Our approach enjoys the best of both worlds: it performs similarly to SGD with random access (even for homogenous data) without compromising the data access efficiency of CorgiPile. We provide a comprehensive theoretical analysis of the convergence properties of our method and demonstrate its practical advantages through experimental results.

Beyond Implicit Bias: The Insignificance of SGD Noise in Online Learning

The success of SGD in deep learning has been ascribed by prior works to the implicit bias induced by high learning rate or small batch size ("SGD noise"). While prior works that focused on offline learning (i.e., multiple-epoch training), we study the impact of SGD noise on online (i.e., single epoch) learning. Through an extensive empirical analysis of image and language data, we demonstrate that large learning rate and small batch size do not confer any implicit bias advantages in online learning. In contrast to offline learning, the benefits of SGD noise in online learning are strictly computational, facilitating larger or more cost-effective gradient steps. Our work suggests that SGD in the online regime can be construed as taking noisy steps along the "golden path" of the noiseless gradient flow algorithm. We provide evidence to support this hypothesis by conducting experiments that reduce SGD noise during training and by measuring the pointwise functional distance between models trained with varying SGD noise levels, but at equivalent loss values. Our findings challenge the prevailing understanding of SGD and offer novel insights into its role in online learning.

SubTuning: Efficient Finetuning for Multi-Task Learning

Finetuning a pretrained model has become a standard approach for training neural networks on novel tasks, resulting in fast convergence and improved performance. In this work, we study an alternative finetuning method, where instead of finetuning all the weights of the network, we only train a carefully chosen subset of layers, keeping the rest of the weights frozen at their initial (pretrained) values. We demonstrate that \emph{subset finetuning} (or SubTuning) often achieves accuracy comparable to full finetuning of the model, and even surpasses the performance of full finetuning when training data is scarce. Therefore, SubTuning allows deploying new tasks at minimal computational cost, while enjoying the benefits of finetuning the entire model. This yields a simple and effective method for multi-task learning, where different tasks do not interfere with one another, and yet share most of the resources at inference time. We demonstrate the efficiency of SubTuning across multiple tasks, using different network architectures and pretraining methods.

Knowledge Distillation: Bad Models Can Be Good Role Models

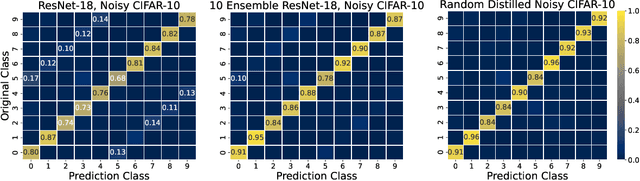
Large neural networks trained in the overparameterized regime are able to fit noise to zero train error. Recent work \citep{nakkiran2020distributional} has empirically observed that such networks behave as "conditional samplers" from the noisy distribution. That is, they replicate the noise in the train data to unseen examples. We give a theoretical framework for studying this conditional sampling behavior in the context of learning theory. We relate the notion of such samplers to knowledge distillation, where a student network imitates the outputs of a teacher on unlabeled data. We show that samplers, while being bad classifiers, can be good teachers. Concretely, we prove that distillation from samplers is guaranteed to produce a student which approximates the Bayes optimal classifier. Finally, we show that some common learning algorithms (e.g., Nearest-Neighbours and Kernel Machines) can generate samplers when applied in the overparameterized regime.

Deconstructing Distributions: A Pointwise Framework of Learning

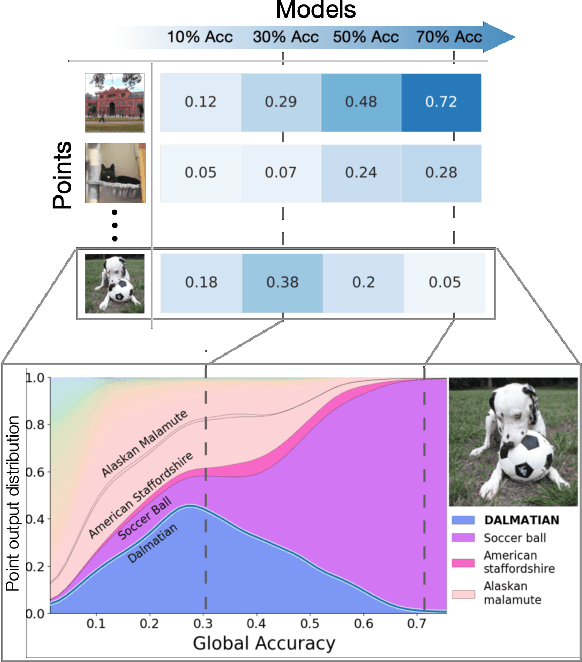
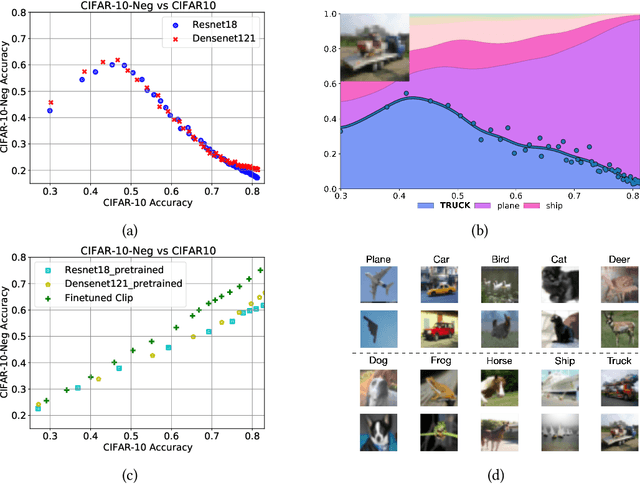
In machine learning, we traditionally evaluate the performance of a single model, averaged over a collection of test inputs. In this work, we propose a new approach: we measure the performance of a collection of models when evaluated on a $\textit{single input point}$. Specifically, we study a point's $\textit{profile}$: the relationship between models' average performance on the test distribution and their pointwise performance on this individual point. We find that profiles can yield new insights into the structure of both models and data -- in and out-of-distribution. For example, we empirically show that real data distributions consist of points with qualitatively different profiles. On one hand, there are "compatible" points with strong correlation between the pointwise and average performance. On the other hand, there are points with weak and even $\textit{negative}$ correlation: cases where improving overall model accuracy actually $\textit{hurts}$ performance on these inputs. We prove that these experimental observations are inconsistent with the predictions of several simplified models of learning proposed in prior work. As an application, we use profiles to construct a dataset we call CIFAR-10-NEG: a subset of CINIC-10 such that for standard models, accuracy on CIFAR-10-NEG is $\textit{negatively correlated}$ with accuracy on CIFAR-10 test. This illustrates, for the first time, an OOD dataset that completely inverts "accuracy-on-the-line" (Miller, Taori, Raghunathan, Sagawa, Koh, Shankar, Liang, Carmon, and Schmidt 2021)

For Manifold Learning, Deep Neural Networks can be Locality Sensitive Hash Functions

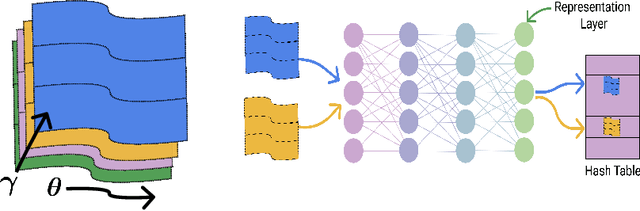
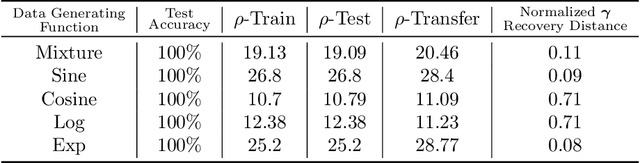
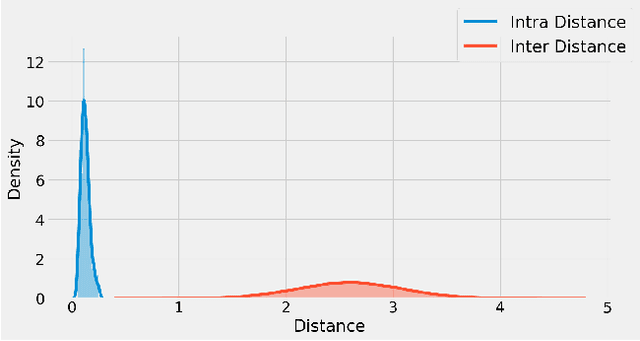
It is well established that training deep neural networks gives useful representations that capture essential features of the inputs. However, these representations are poorly understood in theory and practice. In the context of supervised learning an important question is whether these representations capture features informative for classification, while filtering out non-informative noisy ones. We explore a formalization of this question by considering a generative process where each class is associated with a high-dimensional manifold and different classes define different manifolds. Under this model, each input is produced using two latent vectors: (i) a "manifold identifier" $\gamma$ and; (ii)~a "transformation parameter" $\theta$ that shifts examples along the surface of a manifold. E.g., $\gamma$ might represent a canonical image of a dog, and $\theta$ might stand for variations in pose, background or lighting. We provide theoretical and empirical evidence that neural representations can be viewed as LSH-like functions that map each input to an embedding that is a function of solely the informative $\gamma$ and invariant to $\theta$, effectively recovering the manifold identifier $\gamma$. An important consequence of this behavior is one-shot learning to unseen classes.

For self-supervised learning, Rationality implies generalization, provably

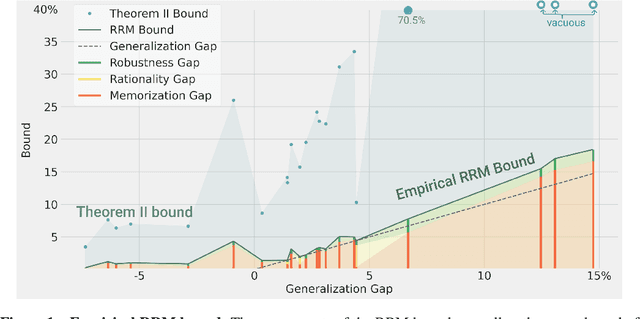
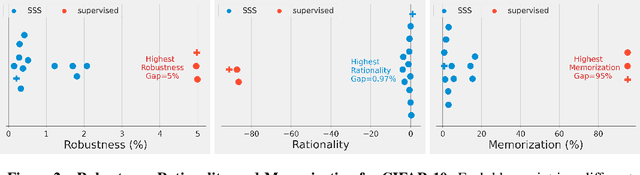
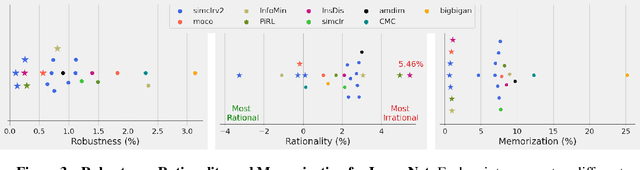
We prove a new upper bound on the generalization gap of classifiers that are obtained by first using self-supervision to learn a representation $r$ of the training data, and then fitting a simple (e.g., linear) classifier $g$ to the labels. Specifically, we show that (under the assumptions described below) the generalization gap of such classifiers tends to zero if $\mathsf{C}(g) \ll n$, where $\mathsf{C}(g)$ is an appropriately-defined measure of the simple classifier $g$'s complexity, and $n$ is the number of training samples. We stress that our bound is independent of the complexity of the representation $r$. We do not make any structural or conditional-independence assumptions on the representation-learning task, which can use the same training dataset that is later used for classification. Rather, we assume that the training procedure satisfies certain natural noise-robustness (adding small amount of label noise causes small degradation in performance) and rationality (getting the wrong label is not better than getting no label at all) conditions that widely hold across many standard architectures. We show that our bound is non-vacuous for many popular representation-learning based classifiers on CIFAR-10 and ImageNet, including SimCLR, AMDIM and MoCo.

Robustness from Simple Classifiers

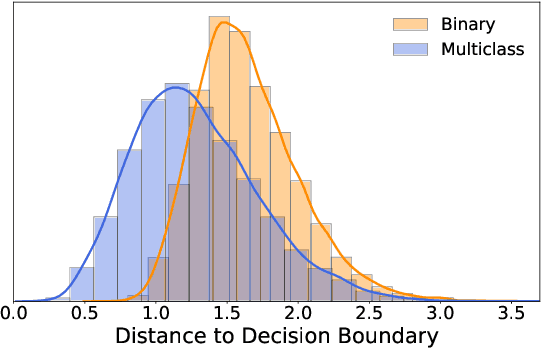
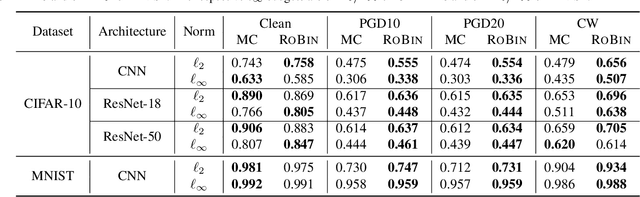
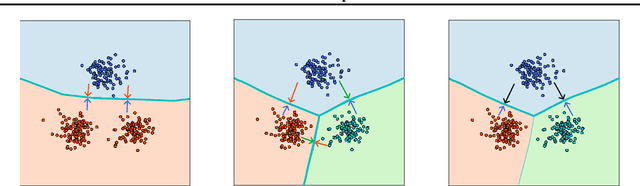
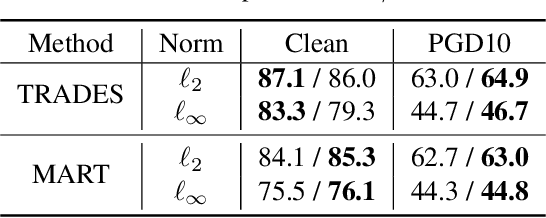
Despite the vast success of Deep Neural Networks in numerous application domains, it has been shown that such models are not robust i.e., they are vulnerable to small adversarial perturbations of the input. While extensive work has been done on why such perturbations occur or how to successfully defend against them, we still do not have a complete understanding of robustness. In this work, we investigate the connection between robustness and simplicity. We find that simpler classifiers, formed by reducing the number of output classes, are less susceptible to adversarial perturbations. Consequently, we demonstrate that decomposing a complex multiclass model into an aggregation of binary models enhances robustness. This behavior is consistent across different datasets and model architectures and can be combined with known defense techniques such as adversarial training. Moreover, we provide further evidence of a disconnect between standard and robust learning regimes. In particular, we show that elaborate label information can help standard accuracy but harm robustness.

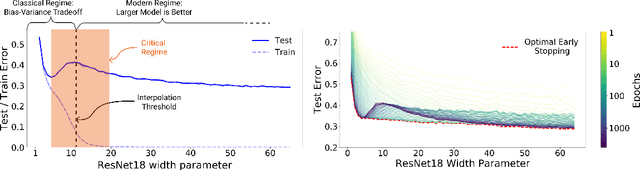
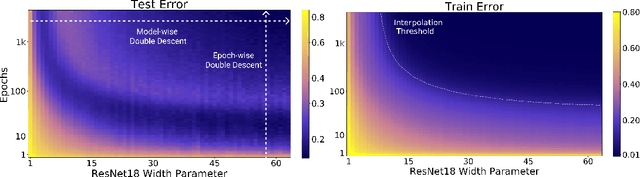
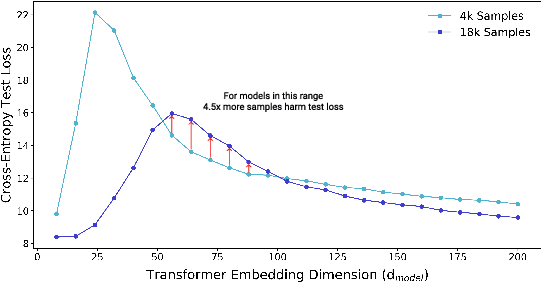
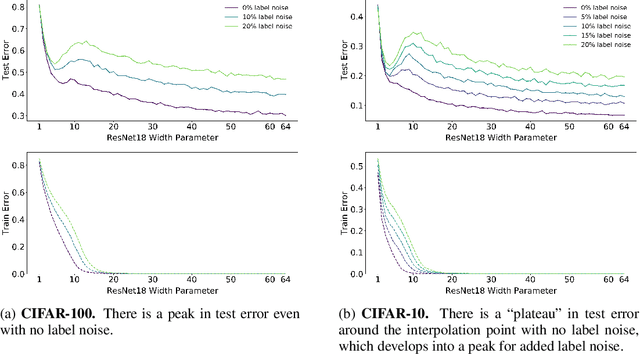
Deep Double Descent: Where Bigger Models and More Data Hurt

We show that a variety of modern deep learning tasks exhibit a "double-descent" phenomenon where, as we increase model size, performance first gets worse and then gets better. Moreover, we show that double descent occurs not just as a function of model size, but also as a function of the number of training epochs. We unify the above phenomena by defining a new complexity measure we call the effective model complexity and conjecture a generalized double descent with respect to this measure. Furthermore, our notion of model complexity allows us to identify certain regimes where increasing (even quadrupling) the number of train samples actually hurts test performance.

SGD on Neural Networks Learns Functions of Increasing Complexity

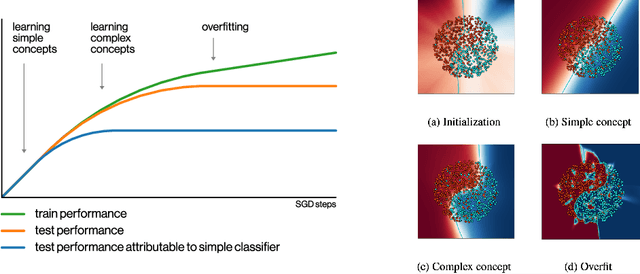
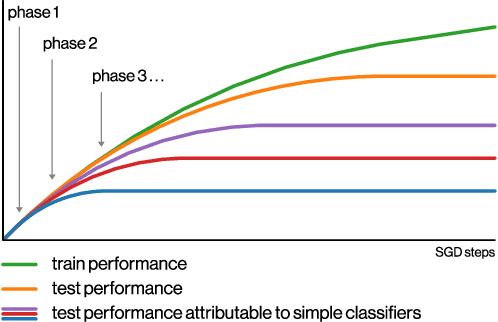
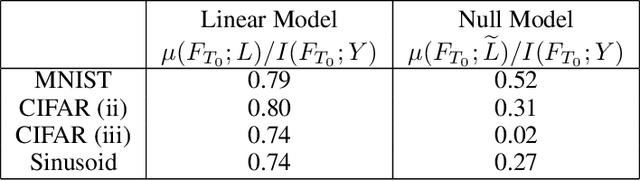
We perform an experimental study of the dynamics of Stochastic Gradient Descent (SGD) in learning deep neural networks for several real and synthetic classification tasks. We show that in the initial epochs, almost all of the performance improvement of the classifier obtained by SGD can be explained by a linear classifier. More generally, we give evidence for the hypothesis that, as iterations progress, SGD learns functions of increasing complexity. This hypothesis can be helpful in explaining why SGD-learned classifiers tend to generalize well even in the over-parameterized regime. We also show that the linear classifier learned in the initial stages is "retained" throughout the execution even if training is continued to the point of zero training error, and complement this with a theoretical result in a simplified model. Key to our work is a new measure of how well one classifier explains the performance of another, based on conditional mutual information.