Aurojit Panda
CLM: Removing the GPU Memory Barrier for 3D Gaussian Splatting
Nov 07, 2025Abstract:3D Gaussian Splatting (3DGS) is an increasingly popular novel view synthesis approach due to its fast rendering time, and high-quality output. However, scaling 3DGS to large (or intricate) scenes is challenging due to its large memory requirement, which exceed most GPU's memory capacity. In this paper, we describe CLM, a system that allows 3DGS to render large scenes using a single consumer-grade GPU, e.g., RTX4090. It does so by offloading Gaussians to CPU memory, and loading them into GPU memory only when necessary. To reduce performance and communication overheads, CLM uses a novel offloading strategy that exploits observations about 3DGS's memory access pattern for pipelining, and thus overlap GPU-to-CPU communication, GPU computation and CPU computation. Furthermore, we also exploit observation about the access pattern to reduce communication volume. Our evaluation shows that the resulting implementation can render a large scene that requires 100 million Gaussians on a single RTX4090 and achieve state-of-the-art reconstruction quality.
Understanding Stragglers in Large Model Training Using What-if Analysis
May 09, 2025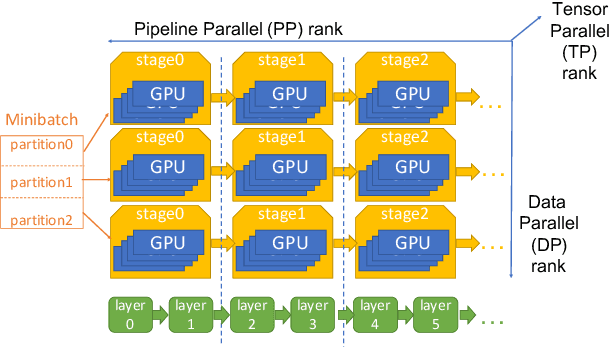

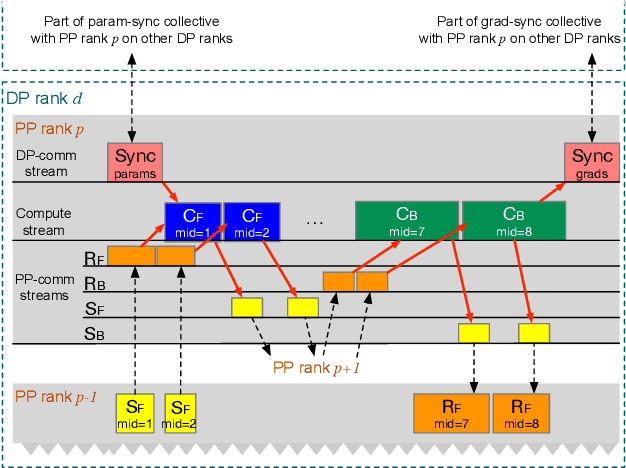
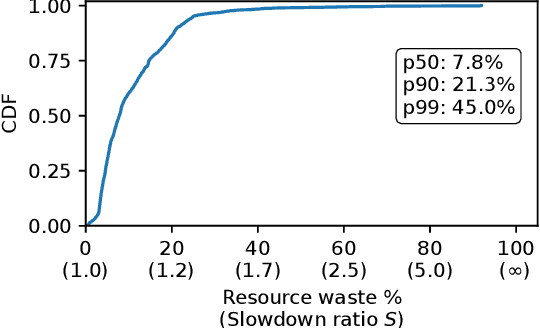
Abstract:Large language model (LLM) training is one of the most demanding distributed computations today, often requiring thousands of GPUs with frequent synchronization across machines. Such a workload pattern makes it susceptible to stragglers, where the training can be stalled by few slow workers. At ByteDance we find stragglers are not trivially always caused by hardware failures, but can arise from multiple complex factors. This work aims to present a comprehensive study on the straggler issues in LLM training, using a five-month trace collected from our ByteDance LLM training cluster. The core methodology is what-if analysis that simulates the scenario without any stragglers and contrasts with the actual case. We use this method to study the following questions: (1) how often do stragglers affect training jobs, and what effect do they have on job performance; (2) do stragglers exhibit temporal or spatial patterns; and (3) what are the potential root causes for stragglers?
Reasoning Models Know When They're Right: Probing Hidden States for Self-Verification
Apr 07, 2025



Abstract:Reasoning models have achieved remarkable performance on tasks like math and logical reasoning thanks to their ability to search during reasoning. However, they still suffer from overthinking, often performing unnecessary reasoning steps even after reaching the correct answer. This raises the question: can models evaluate the correctness of their intermediate answers during reasoning? In this work, we study whether reasoning models encode information about answer correctness through probing the model's hidden states. The resulting probe can verify intermediate answers with high accuracy and produces highly calibrated scores. Additionally, we find models' hidden states encode correctness of future answers, enabling early prediction of the correctness before the intermediate answer is fully formulated. We then use the probe as a verifier to decide whether to exit reasoning at intermediate answers during inference, reducing the number of inference tokens by 24\% without compromising performance. These findings confirm that reasoning models do encode a notion of correctness yet fail to exploit it, revealing substantial untapped potential to enhance their efficiency.
On Scaling Up 3D Gaussian Splatting Training
Jun 26, 2024



Abstract:3D Gaussian Splatting (3DGS) is increasingly popular for 3D reconstruction due to its superior visual quality and rendering speed. However, 3DGS training currently occurs on a single GPU, limiting its ability to handle high-resolution and large-scale 3D reconstruction tasks due to memory constraints. We introduce Grendel, a distributed system designed to partition 3DGS parameters and parallelize computation across multiple GPUs. As each Gaussian affects a small, dynamic subset of rendered pixels, Grendel employs sparse all-to-all communication to transfer the necessary Gaussians to pixel partitions and performs dynamic load balancing. Unlike existing 3DGS systems that train using one camera view image at a time, Grendel supports batched training with multiple views. We explore various optimization hyperparameter scaling strategies and find that a simple sqrt(batch size) scaling rule is highly effective. Evaluations using large-scale, high-resolution scenes show that Grendel enhances rendering quality by scaling up 3DGS parameters across multiple GPUs. On the Rubble dataset, we achieve a test PSNR of 27.28 by distributing 40.4 million Gaussians across 16 GPUs, compared to a PSNR of 26.28 using 11.2 million Gaussians on a single GPU. Grendel is an open-source project available at: https://github.com/nyu-systems/Grendel-GS
Finding Deep-Learning Compilation Bugs with NNSmith
Jul 26, 2022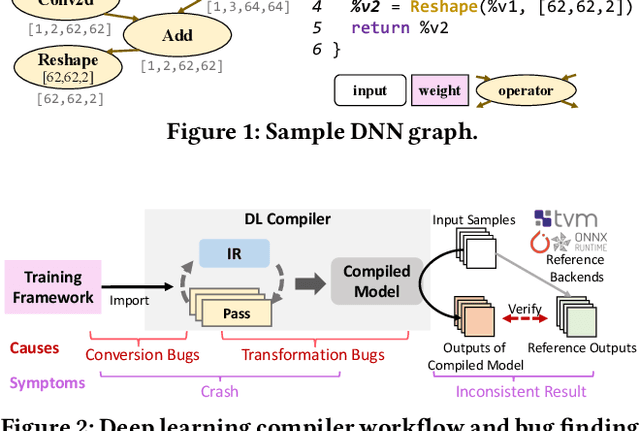


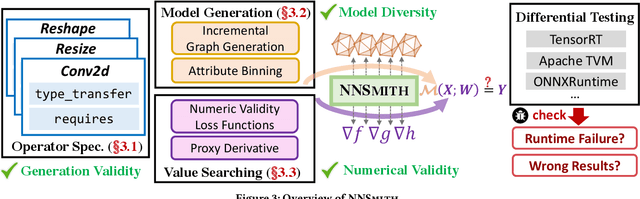
Abstract:Deep-learning (DL) compilers such as TVM and TensorRT are increasingly used to optimize deep neural network (DNN) models to meet performance, resource utilization and other requirements. Bugs in these compilers can produce optimized models whose semantics differ from the original models, and produce incorrect results impacting the correctness of down stream applications. However, finding bugs in these compilers is challenging due to their complexity. In this work, we propose a new fuzz testing approach for finding bugs in deep-learning compilers. Our core approach uses (i) light-weight operator specifications to generate diverse yet valid DNN models allowing us to exercise a large part of the compiler's transformation logic; (ii) a gradient-based search process for finding model inputs that avoid any floating-point exceptional values during model execution, reducing the chance of missed bugs or false alarms; and (iii) differential testing to identify bugs. We implemented this approach in NNSmith which has found 65 new bugs in the last seven months for TVM, TensorRT, ONNXRuntime, and PyTorch. Of these 52 have been confirmed and 44 have been fixed by project maintainers.
Measuring the Effect of Training Data on Deep Learning Predictions via Randomized Experiments
Jun 20, 2022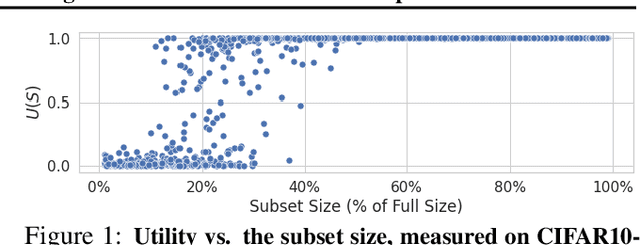
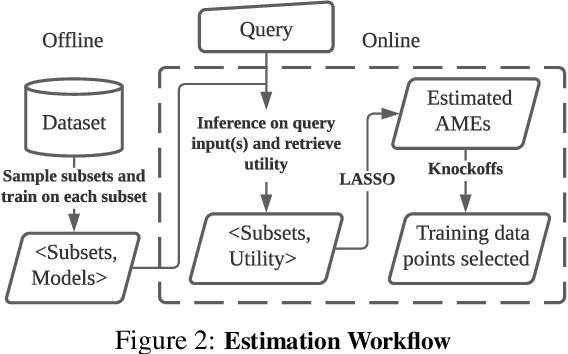

Abstract:We develop a new, principled algorithm for estimating the contribution of training data points to the behavior of a deep learning model, such as a specific prediction it makes. Our algorithm estimates the AME, a quantity that measures the expected (average) marginal effect of adding a data point to a subset of the training data, sampled from a given distribution. When subsets are sampled from the uniform distribution, the AME reduces to the well-known Shapley value. Our approach is inspired by causal inference and randomized experiments: we sample different subsets of the training data to train multiple submodels, and evaluate each submodel's behavior. We then use a LASSO regression to jointly estimate the AME of each data point, based on the subset compositions. Under sparsity assumptions ($k \ll N$ datapoints have large AME), our estimator requires only $O(k\log N)$ randomized submodel trainings, improving upon the best prior Shapley value estimators.
How to Train your DNN: The Network Operator Edition
Apr 21, 2020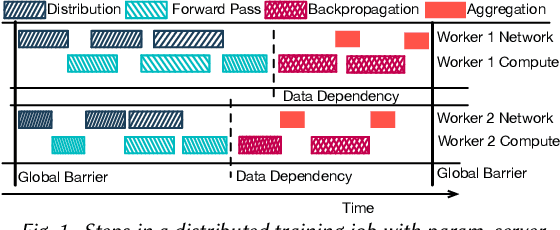
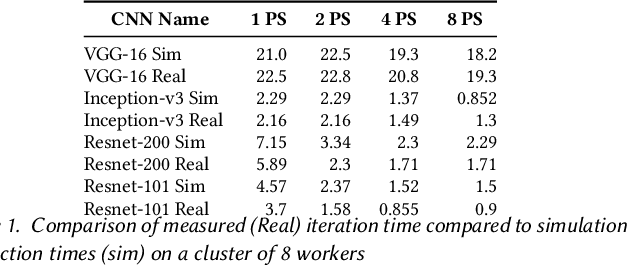
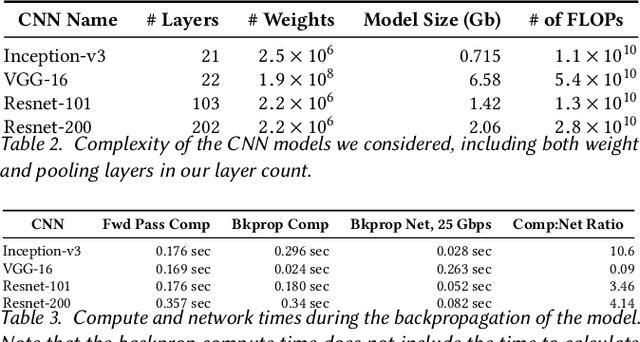
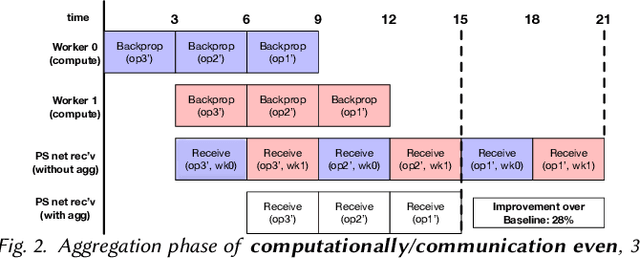
Abstract:Deep Neural Nets have hit quite a crest, But physical networks are where they must rest, And here we put them all to the test, To see which network optimization is best.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge