Reasoning Models Know When They're Right: Probing Hidden States for Self-Verification

Reasoning models have achieved remarkable performance on tasks like math and logical reasoning thanks to their ability to search during reasoning. However, they still suffer from overthinking, often performing unnecessary reasoning steps even after reaching the correct answer. This raises the question: can models evaluate the correctness of their intermediate answers during reasoning? In this work, we study whether reasoning models encode information about answer correctness through probing the model's hidden states. The resulting probe can verify intermediate answers with high accuracy and produces highly calibrated scores. Additionally, we find models' hidden states encode correctness of future answers, enabling early prediction of the correctness before the intermediate answer is fully formulated. We then use the probe as a verifier to decide whether to exit reasoning at intermediate answers during inference, reducing the number of inference tokens by 24\% without compromising performance. These findings confirm that reasoning models do encode a notion of correctness yet fail to exploit it, revealing substantial untapped potential to enhance their efficiency.

CoMBO: Conflict Mitigation via Branched Optimization for Class Incremental Segmentation

Effective Class Incremental Segmentation (CIS) requires simultaneously mitigating catastrophic forgetting and ensuring sufficient plasticity to integrate new classes. The inherent conflict above often leads to a back-and-forth, which turns the objective into finding the balance between the performance of previous~(old) and incremental~(new) classes. To address this conflict, we introduce a novel approach, Conflict Mitigation via Branched Optimization~(CoMBO). Within this approach, we present the Query Conflict Reduction module, designed to explicitly refine queries for new classes through lightweight, class-specific adapters. This module provides an additional branch for the acquisition of new classes while preserving the original queries for distillation. Moreover, we develop two strategies to further mitigate the conflict following the branched structure, \textit{i.e.}, the Half-Learning Half-Distillation~(HDHL) over classification probabilities, and the Importance-Based Knowledge Distillation~(IKD) over query features. HDHL selectively engages in learning for classification probabilities of queries that match the ground truth of new classes, while aligning unmatched ones to the corresponding old probabilities, thus ensuring retention of old knowledge while absorbing new classes via learning negative samples. Meanwhile, IKD assesses the importance of queries based on their matching degree to old classes, prioritizing the distillation of important features and allowing less critical features to evolve. Extensive experiments in Class Incremental Panoptic and Semantic Segmentation settings have demonstrated the superior performance of CoMBO. Project page: https://guangyu-ryan.github.io/CoMBO.

Bridge the Points: Graph-based Few-shot Segment Anything Semantically

The recent advancements in large-scale pre-training techniques have significantly enhanced the capabilities of vision foundation models, notably the Segment Anything Model (SAM), which can generate precise masks based on point and box prompts. Recent studies extend SAM to Few-shot Semantic Segmentation (FSS), focusing on prompt generation for SAM-based automatic semantic segmentation. However, these methods struggle with selecting suitable prompts, require specific hyperparameter settings for different scenarios, and experience prolonged one-shot inference times due to the overuse of SAM, resulting in low efficiency and limited automation ability. To address these issues, we propose a simple yet effective approach based on graph analysis. In particular, a Positive-Negative Alignment module dynamically selects the point prompts for generating masks, especially uncovering the potential of the background context as the negative reference. Another subsequent Point-Mask Clustering module aligns the granularity of masks and selected points as a directed graph, based on mask coverage over points. These points are then aggregated by decomposing the weakly connected components of the directed graph in an efficient manner, constructing distinct natural clusters. Finally, the positive and overshooting gating, benefiting from graph-based granularity alignment, aggregate high-confident masks and filter out the false-positive masks for final prediction, reducing the usage of additional hyperparameters and redundant mask generation. Extensive experimental analysis across standard FSS, One-shot Part Segmentation, and Cross Domain FSS datasets validate the effectiveness and efficiency of the proposed approach, surpassing state-of-the-art generalist models with a mIoU of 58.7% on COCO-20i and 35.2% on LVIS-92i. The code is available in https://andyzaq.github.io/GF-SAM/.

Optimal Visual Search with Highly Heuristic Decision Rules

Visual search is a fundamental natural task for humans and other animals. We investigated the decision processes humans use when searching briefly presented displays having well-separated potential target-object locations. Performance was compared with the Bayesian-optimal decision process under the assumption that the information from the different potential target locations is statistically independent. Surprisingly, humans performed slightly better than optimal, despite humans' substantial loss of sensitivity in the fovea, and the implausibility of the human brain replicating the optimal computations. We show that three factors can quantitatively explain these seemingly paradoxical results. Most importantly, simple and fixed heuristic decision rules reach near optimal search performance. Secondly, foveal neglect primarily affects only the central potential target location. Finally, spatially correlated neural noise causes search performance to exceed that predicted for independent noise. These findings have far-reaching implications for understanding visual search tasks and other identification tasks in humans and other animals.

Structure-enhanced Contrastive Learning for Graph Clustering

Graph clustering is a crucial task in network analysis with widespread applications, focusing on partitioning nodes into distinct groups with stronger intra-group connections than inter-group ones. Recently, contrastive learning has achieved significant progress in graph clustering. However, most methods suffer from the following issues: 1) an over-reliance on meticulously designed data augmentation strategies, which can undermine the potential of contrastive learning. 2) overlooking cluster-oriented structural information, particularly the higher-order cluster(community) structure information, which could unveil the mesoscopic cluster structure information of the network. In this study, Structure-enhanced Contrastive Learning (SECL) is introduced to addresses these issues by leveraging inherent network structures. SECL utilizes a cross-view contrastive learning mechanism to enhance node embeddings without elaborate data augmentations, a structural contrastive learning module for ensuring structural consistency, and a modularity maximization strategy for harnessing clustering-oriented information. This comprehensive approach results in robust node representations that greatly enhance clustering performance. Extensive experiments on six datasets confirm SECL's superiority over current state-of-the-art methods, indicating a substantial improvement in the domain of graph clustering.

Adaptive Pre-training Data Detection for Large Language Models via Surprising Tokens

While large language models (LLMs) are extensively used, there are raising concerns regarding privacy, security, and copyright due to their opaque training data, which brings the problem of detecting pre-training data on the table. Current solutions to this problem leverage techniques explored in machine learning privacy such as Membership Inference Attacks (MIAs), which heavily depend on LLMs' capability of verbatim memorization. However, this reliance presents challenges, especially given the vast amount of training data and the restricted number of effective training epochs. In this paper, we propose an adaptive pre-training data detection method which alleviates this reliance and effectively amplify the identification. Our method adaptively locates \textit{surprising tokens} of the input. A token is surprising to a LLM if the prediction on the token is "certain but wrong", which refers to low Shannon entropy of the probability distribution and low probability of the ground truth token at the same time. By using the prediction probability of surprising tokens to measure \textit{surprising}, the detection method is achieved based on the simple hypothesis that seeing seen data is less surprising for the model compared with seeing unseen data. The method can be applied without any access to the the pre-training data corpus or additional training like reference models. Our approach exhibits a consistent enhancement compared to existing methods in diverse experiments conducted on various benchmarks and models, achieving a maximum improvement of 29.5\%. We also introduce a new benchmark Dolma-Book developed upon a novel framework, which employs book data collected both before and after model training to provide further evaluation.

Background Adaptation with Residual Modeling for Exemplar-Free Class-Incremental Semantic Segmentation

Class Incremental Semantic Segmentation~(CISS), within Incremental Learning for semantic segmentation, targets segmenting new categories while reducing the catastrophic forgetting on the old categories.Besides, background shifting, where the background category changes constantly in each step, is a special challenge for CISS. Current methods with a shared background classifier struggle to keep up with these changes, leading to decreased stability in background predictions and reduced accuracy of segmentation. For this special challenge, we designed a novel background adaptation mechanism, which explicitly models the background residual rather than the background itself in each step, and aggregates these residuals to represent the evolving background. Therefore, the background adaptation mechanism ensures the stability of previous background classifiers, while enabling the model to concentrate on the easy-learned residuals from the additional channel, which enhances background discernment for better prediction of novel categories. To precisely optimize the background adaptation mechanism, we propose Pseudo Background Binary Cross-Entropy loss and Background Adaptation losses, which amplify the adaptation effect. Group Knowledge Distillation and Background Feature Distillation strategies are designed to prevent forgetting old categories. Our approach, evaluated across various incremental scenarios on Pascal VOC 2012 and ADE20K datasets, outperforms prior exemplar-free state-of-the-art methods with mIoU of 3.0% in VOC 10-1 and 2.0% in ADE 100-5, notably enhancing the accuracy of new classes while mitigating catastrophic forgetting. Code is available in https://andyzaq.github.io/barmsite/.

Measuring the Effect of Training Data on Deep Learning Predictions via Randomized Experiments

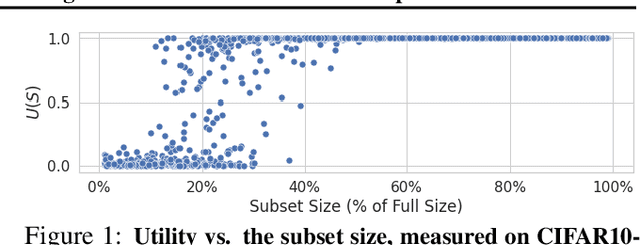
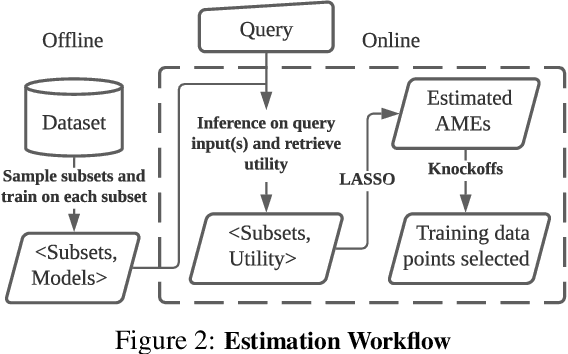
We develop a new, principled algorithm for estimating the contribution of training data points to the behavior of a deep learning model, such as a specific prediction it makes. Our algorithm estimates the AME, a quantity that measures the expected (average) marginal effect of adding a data point to a subset of the training data, sampled from a given distribution. When subsets are sampled from the uniform distribution, the AME reduces to the well-known Shapley value. Our approach is inspired by causal inference and randomized experiments: we sample different subsets of the training data to train multiple submodels, and evaluate each submodel's behavior. We then use a LASSO regression to jointly estimate the AME of each data point, based on the subset compositions. Under sparsity assumptions ($k \ll N$ datapoints have large AME), our estimator requires only $O(k\log N)$ randomized submodel trainings, improving upon the best prior Shapley value estimators.