Demystifying Data-Driven Probabilistic Medium-Range Weather Forecasting

The recent revolution in data-driven methods for weather forecasting has lead to a fragmented landscape of complex, bespoke architectures and training strategies, obscuring the fundamental drivers of forecast accuracy. Here, we demonstrate that state-of-the-art probabilistic skill requires neither intricate architectural constraints nor specialized training heuristics. We introduce a scalable framework for learning multi-scale atmospheric dynamics by combining a directly downsampled latent space with a history-conditioned local projector that resolves high-resolution physics. We find that our framework design is robust to the choice of probabilistic estimator, seamlessly supporting stochastic interpolants, diffusion models, and CRPS-based ensemble training. Validated against the Integrated Forecasting System and the deep learning probabilistic model GenCast, our framework achieves statistically significant improvements on most of the variables. These results suggest scaling a general-purpose model is sufficient for state-of-the-art medium-range prediction, eliminating the need for tailored training recipes and proving effective across the full spectrum of probabilistic frameworks.

Transition Matching Distillation for Fast Video Generation

Large video diffusion and flow models have achieved remarkable success in high-quality video generation, but their use in real-time interactive applications remains limited due to their inefficient multi-step sampling process. In this work, we present Transition Matching Distillation (TMD), a novel framework for distilling video diffusion models into efficient few-step generators. The central idea of TMD is to match the multi-step denoising trajectory of a diffusion model with a few-step probability transition process, where each transition is modeled as a lightweight conditional flow. To enable efficient distillation, we decompose the original diffusion backbone into two components: (1) a main backbone, comprising the majority of early layers, that extracts semantic representations at each outer transition step; and (2) a flow head, consisting of the last few layers, that leverages these representations to perform multiple inner flow updates. Given a pretrained video diffusion model, we first introduce a flow head to the model, and adapt it into a conditional flow map. We then apply distribution matching distillation to the student model with flow head rollout in each transition step. Extensive experiments on distilling Wan2.1 1.3B and 14B text-to-video models demonstrate that TMD provides a flexible and strong trade-off between generation speed and visual quality. In particular, TMD outperforms existing distilled models under comparable inference costs in terms of visual fidelity and prompt adherence. Project page: https://research.nvidia.com/labs/genair/tmd

Rethinking Molecule Synthesizability with Chain-of-Reaction

A well-known pitfall of molecular generative models is that they are not guaranteed to generate synthesizable molecules. There have been considerable attempts to address this problem, but given the exponentially large combinatorial space of synthesizable molecules, existing methods have shown limited coverage of the space and poor molecular optimization performance. To tackle these problems, we introduce ReaSyn, a generative framework for synthesizable projection where the model explores the neighborhood of given molecules in the synthesizable space by generating pathways that result in synthesizable analogs. To fully utilize the chemical knowledge contained in the synthetic pathways, we propose a novel perspective that views synthetic pathways akin to reasoning paths in large language models (LLMs). Specifically, inspired by chain-of-thought (CoT) reasoning in LLMs, we introduce the chain-of-reaction (CoR) notation that explicitly states reactants, reaction types, and intermediate products for each step in a pathway. With the CoR notation, ReaSyn can get dense supervision in every reaction step to explicitly learn chemical reaction rules during supervised training and perform step-by-step reasoning. In addition, to further enhance the reasoning capability of ReaSyn, we propose reinforcement learning (RL)-based finetuning and goal-directed test-time compute scaling tailored for synthesizable projection. ReaSyn achieves the highest reconstruction rate and pathway diversity in synthesizable molecule reconstruction and the highest optimization performance in synthesizable goal-directed molecular optimization, and significantly outperforms previous synthesizable projection methods in synthesizable hit expansion. These results highlight ReaSyn's superior ability to navigate combinatorially-large synthesizable chemical space.

Trust Region Constrained Measure Transport in Path Space for Stochastic Optimal Control and Inference

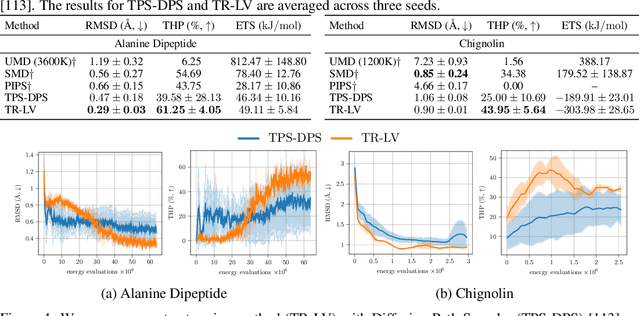
Solving stochastic optimal control problems with quadratic control costs can be viewed as approximating a target path space measure, e.g. via gradient-based optimization. In practice, however, this optimization is challenging in particular if the target measure differs substantially from the prior. In this work, we therefore approach the problem by iteratively solving constrained problems incorporating trust regions that aim for approaching the target measure gradually in a systematic way. It turns out that this trust region based strategy can be understood as a geometric annealing from the prior to the target measure, where, however, the incorporated trust regions lead to a principled and educated way of choosing the time steps in the annealing path. We demonstrate in multiple optimal control applications that our novel method can improve performance significantly, including tasks in diffusion-based sampling, transition path sampling, and fine-tuning of diffusion models.

EquiVDM: Equivariant Video Diffusion Models with Temporally Consistent Noise

Temporally consistent video-to-video generation is essential for applications of video diffusion models in areas such as sim-to-real, style-transfer, video upsampling, etc. In this paper, we propose a video diffusion framework that leverages temporally consistent noise to generate coherent video frames without specialized modules or additional constraints. We show that the standard training objective of diffusion models, when applied with temporally consistent noise, encourages the model to be equivariant to spatial transformations in input video and noise. This enables our model to better follow motion patterns from the input video, producing aligned motion and high-fidelity frames. Furthermore, we extend our approach to 3D-consistent video generation by attaching noise as textures on 3D meshes, ensuring 3D consistency in sim-to-real applications. Experimental results demonstrate that our method surpasses state-of-the-art baselines in motion alignment, 3D consistency, and video quality while requiring only a few sampling steps in practice.

One-step Diffusion Models with $f$-Divergence Distribution Matching

Sampling from diffusion models involves a slow iterative process that hinders their practical deployment, especially for interactive applications. To accelerate generation speed, recent approaches distill a multi-step diffusion model into a single-step student generator via variational score distillation, which matches the distribution of samples generated by the student to the teacher's distribution. However, these approaches use the reverse Kullback-Leibler (KL) divergence for distribution matching which is known to be mode seeking. In this paper, we generalize the distribution matching approach using a novel $f$-divergence minimization framework, termed $f$-distill, that covers different divergences with different trade-offs in terms of mode coverage and training variance. We derive the gradient of the $f$-divergence between the teacher and student distributions and show that it is expressed as the product of their score differences and a weighting function determined by their density ratio. This weighting function naturally emphasizes samples with higher density in the teacher distribution, when using a less mode-seeking divergence. We observe that the popular variational score distillation approach using the reverse-KL divergence is a special case within our framework. Empirically, we demonstrate that alternative $f$-divergences, such as forward-KL and Jensen-Shannon divergences, outperform the current best variational score distillation methods across image generation tasks. In particular, when using Jensen-Shannon divergence, $f$-distill achieves current state-of-the-art one-step generation performance on ImageNet64 and zero-shot text-to-image generation on MS-COCO. Project page: https://research.nvidia.com/labs/genair/f-distill

Not-So-Optimal Transport Flows for 3D Point Cloud Generation

Learning generative models of 3D point clouds is one of the fundamental problems in 3D generative learning. One of the key properties of point clouds is their permutation invariance, i.e., changing the order of points in a point cloud does not change the shape they represent. In this paper, we analyze the recently proposed equivariant OT flows that learn permutation invariant generative models for point-based molecular data and we show that these models scale poorly on large point clouds. Also, we observe learning (equivariant) OT flows is generally challenging since straightening flow trajectories makes the learned flow model complex at the beginning of the trajectory. To remedy these, we propose not-so-optimal transport flow models that obtain an approximate OT by an offline OT precomputation, enabling an efficient construction of OT pairs for training. During training, we can additionally construct a hybrid coupling by combining our approximate OT and independent coupling to make the target flow models easier to learn. In an extensive empirical study, we show that our proposed model outperforms prior diffusion- and flow-based approaches on a wide range of unconditional generation and shape completion on the ShapeNet benchmark.

A2SB: Audio-to-Audio Schrodinger Bridges

Audio in the real world may be perturbed due to numerous factors, causing the audio quality to be degraded. The following work presents an audio restoration model tailored for high-res music at 44.1kHz. Our model, Audio-to-Audio Schrodinger Bridges (A2SB), is capable of both bandwidth extension (predicting high-frequency components) and inpainting (re-generating missing segments). Critically, A2SB is end-to-end without need of a vocoder to predict waveform outputs, able to restore hour-long audio inputs, and trained on permissively licensed music data. A2SB is capable of achieving state-of-the-art bandwidth extension and inpainting quality on several out-of-distribution music test sets. Our demo website is https: //research.nvidia.com/labs/adlr/A2SB/.

BlobGEN-Vid: Compositional Text-to-Video Generation with Blob Video Representations

Existing video generation models struggle to follow complex text prompts and synthesize multiple objects, raising the need for additional grounding input for improved controllability. In this work, we propose to decompose videos into visual primitives - blob video representation, a general representation for controllable video generation. Based on blob conditions, we develop a blob-grounded video diffusion model named BlobGEN-Vid that allows users to control object motions and fine-grained object appearance. In particular, we introduce a masked 3D attention module that effectively improves regional consistency across frames. In addition, we introduce a learnable module to interpolate text embeddings so that users can control semantics in specific frames and obtain smooth object transitions. We show that our framework is model-agnostic and build BlobGEN-Vid based on both U-Net and DiT-based video diffusion models. Extensive experimental results show that BlobGEN-Vid achieves superior zero-shot video generation ability and state-of-the-art layout controllability on multiple benchmarks. When combined with an LLM for layout planning, our framework even outperforms proprietary text-to-video generators in terms of compositional accuracy.

GenMol: A Drug Discovery Generalist with Discrete Diffusion

Drug discovery is a complex process that involves multiple scenarios and stages, such as fragment-constrained molecule generation, hit generation and lead optimization. However, existing molecular generative models can only tackle one or two of these scenarios and lack the flexibility to address various aspects of the drug discovery pipeline. In this paper, we present Generalist Molecular generative model (GenMol), a versatile framework that addresses these limitations by applying discrete diffusion to the Sequential Attachment-based Fragment Embedding (SAFE) molecular representation. GenMol generates SAFE sequences through non-autoregressive bidirectional parallel decoding, thereby allowing utilization of a molecular context that does not rely on the specific token ordering and enhanced computational efficiency. Moreover, under the discrete diffusion framework, we introduce fragment remasking, a strategy that optimizes molecules by replacing fragments with masked tokens and regenerating them, enabling effective exploration of chemical space. GenMol significantly outperforms the previous GPT-based model trained on SAFE representations in de novo generation and fragment-constrained generation, and achieves state-of-the-art performance in goal-directed hit generation and lead optimization. These experimental results demonstrate that GenMol can tackle a wide range of drug discovery tasks, providing a unified and versatile approach for molecular design.