Reinforce Adjoint Matching: Scaling RL Post-Training of Diffusion and Flow-Matching Models

Diffusion and flow-matching models scale because pretraining is supervised regression: a clean sample is noised analytically, and a model regresses against a closed-form target. RL post-training aligns the model with a reward. In image generation, this makes samples compose objects correctly, render text legibly, and match human preferences. Existing methods rely on costly SDE rollouts, reward gradients, or surrogate losses, sacrificing pretraining's regression structure. We show that the structure extends to RL post-training. Under KL-regularized reward maximization, the optimal generative process tilts the clean-endpoint distribution towards samples with higher reward and leaves the noising law unchanged. Combining this with the adjoint-matching optimality condition and a REINFORCE identity, we derive Reinforce Adjoint Matching (RAM): a consistency loss that corrects the pretraining target with the reward. At each step, we draw a clean endpoint from the current model, evaluate its reward, noise it as in pretraining, and regress. No SDE rollouts, backward adjoint sweeps, or reward gradients are required. Like the pretraining objective, RAM is simple and scales. On Stable Diffusion 3.5M, RAM achieves the highest reward on composability, text rendering, and human preference, reaching Flow-GRPO's peak reward in up to $50\times$ fewer training steps.

Rare Event Analysis via Stochastic Optimal Control

Rare events such as conformational changes in biomolecules, phase transitions, and chemical reactions are central to the behavior of many physical systems, yet they are extremely difficult to study computationally because unbiased simulations seldom produce them. Transition Path Theory (TPT) provides a rigorous statistical framework for analyzing such events: it characterizes the ensemble of reactive trajectories between two designated metastable states (reactant and product), and its central object--the committor function, which gives the probability that the system will next reach the product rather than the reactant--encodes all essential kinetic and thermodynamic information. We introduce a framework that casts committor estimation as a stochastic optimal control (SOC) problem. In this formulation the committor defines a feedback control--proportional to the gradient of its logarithm--that actively steers trajectories toward the reactive region, thereby enabling efficient sampling of reactive paths. To solve the resulting hitting-time control problem we develop two complementary objectives: a direct backpropagation loss and a principled off-policy Value Matching loss, for which we establish first-order optimality guarantees. We further address metastability, which can trap controlled trajectories in intermediate basins, by introducing an alternative sampling process that preserves the reactive current while lowering effective energy barriers. On benchmark systems, the framework yields markedly more accurate committor estimates, reaction rates, and equilibrium constants than existing methods.

Matching Features, Not Tokens: Energy-Based Fine-Tuning of Language Models

Cross-entropy (CE) training provides dense and scalable supervision for language models, but it optimizes next-token prediction under teacher forcing rather than sequence-level behavior under model rollouts. We introduce a feature-matching objective for language-model fine-tuning that targets sequence-level statistics of the completion distribution, providing dense semantic feedback without requiring a task-specific verifier or preference model. To optimize this objective efficiently, we propose energy-based fine-tuning (EBFT), which uses strided block-parallel sampling to generate multiple rollouts from nested prefixes concurrently, batches feature extraction over these rollouts, and uses the resulting embeddings to perform an on-policy policy-gradient update. We present a theoretical perspective connecting EBFT to KL-regularized feature-matching and energy-based modeling. Empirically, across Q&A coding, unstructured coding, and translation, EBFT matches RLVR and outperforms SFT on downstream accuracy while achieving a lower validation cross-entropy than both methods.

Reject, Resample, Repeat: Understanding Parallel Reasoning in Language Model Inference

Inference-time methods that aggregate and prune multiple samples have emerged as a powerful paradigm for steering large language models, yet we lack any principled understanding of their accuracy-cost tradeoffs. In this paper, we introduce a route to rigorously study such approaches using the lens of *particle filtering* algorithms such as Sequential Monte Carlo (SMC). Given a base language model and a *process reward model* estimating expected terminal rewards, we ask: *how accurately can we sample from a target distribution given some number of process reward evaluations?* Theoretically, we identify (1) simple criteria enabling non-asymptotic guarantees for SMC; (2) algorithmic improvements to SMC; and (3) a fundamental limit faced by all particle filtering methods. Empirically, we demonstrate that our theoretical criteria effectively govern the *sampling error* of SMC, though not necessarily its final *accuracy*, suggesting that theoretical perspectives beyond sampling may be necessary.

Trust Region Constrained Measure Transport in Path Space for Stochastic Optimal Control and Inference

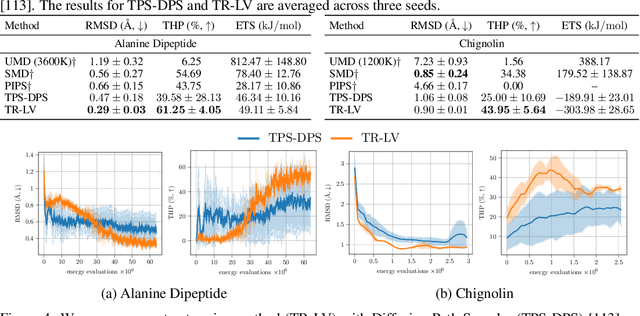
Solving stochastic optimal control problems with quadratic control costs can be viewed as approximating a target path space measure, e.g. via gradient-based optimization. In practice, however, this optimization is challenging in particular if the target measure differs substantially from the prior. In this work, we therefore approach the problem by iteratively solving constrained problems incorporating trust regions that aim for approaching the target measure gradually in a systematic way. It turns out that this trust region based strategy can be understood as a geometric annealing from the prior to the target measure, where, however, the incorporated trust regions lead to a principled and educated way of choosing the time steps in the annealing path. We demonstrate in multiple optimal control applications that our novel method can improve performance significantly, including tasks in diffusion-based sampling, transition path sampling, and fine-tuning of diffusion models.

Adjoint Sampling: Highly Scalable Diffusion Samplers via Adjoint Matching

We introduce Adjoint Sampling, a highly scalable and efficient algorithm for learning diffusion processes that sample from unnormalized densities, or energy functions. It is the first on-policy approach that allows significantly more gradient updates than the number of energy evaluations and model samples, allowing us to scale to much larger problem settings than previously explored by similar methods. Our framework is theoretically grounded in stochastic optimal control and shares the same theoretical guarantees as Adjoint Matching, being able to train without the need for corrective measures that push samples towards the target distribution. We show how to incorporate key symmetries, as well as periodic boundary conditions, for modeling molecules in both cartesian and torsional coordinates. We demonstrate the effectiveness of our approach through extensive experiments on classical energy functions, and further scale up to neural network-based energy models where we perform amortized conformer generation across many molecular systems. To encourage further research in developing highly scalable sampling methods, we plan to open source these challenging benchmarks, where successful methods can directly impact progress in computational chemistry.

Conditioning Diffusions Using Malliavin Calculus

In stochastic optimal control and conditional generative modelling, a central computational task is to modify a reference diffusion process to maximise a given terminal-time reward. Most existing methods require this reward to be differentiable, using gradients to steer the diffusion towards favourable outcomes. However, in many practical settings, like diffusion bridges, the reward is singular, taking an infinite value if the target is hit and zero otherwise. We introduce a novel framework, based on Malliavin calculus and path-space integration by parts, that enables the development of methods robust to such singular rewards. This allows our approach to handle a broad range of applications, including classification, diffusion bridges, and conditioning without the need for artificial observational noise. We demonstrate that our approach offers stable and reliable training, outperforming existing techniques.

Cheap Permutation Testing

Permutation tests are a popular choice for distinguishing distributions and testing independence, due to their exact, finite-sample control of false positives and their minimax optimality when paired with U-statistics. However, standard permutation tests are also expensive, requiring a test statistic to be computed hundreds or thousands of times to detect a separation between distributions. In this work, we offer a simple approach to accelerate testing: group your datapoints into bins and permute only those bins. For U and V-statistics, we prove that these cheap permutation tests have two remarkable properties. First, by storing appropriate sufficient statistics, a cheap test can be run in time comparable to evaluating a single test statistic. Second, cheap permutation power closely approximates standard permutation power. As a result, cheap tests inherit the exact false positive control and minimax optimality of standard permutation tests while running in a fraction of the time. We complement these findings with improved power guarantees for standard permutation testing and experiments demonstrating the benefits of cheap permutations over standard maximum mean discrepancy (MMD), Hilbert-Schmidt independence criterion (HSIC), random Fourier feature, Wilcoxon-Mann-Whitney, cross-MMD, and cross-HSIC tests.

Adjoint Matching: Fine-tuning Flow and Diffusion Generative Models with Memoryless Stochastic Optimal Control

Dynamical generative models that produce samples through an iterative process, such as Flow Matching and denoising diffusion models, have seen widespread use, but there has not been many theoretically-sound methods for improving these models with reward fine-tuning. In this work, we cast reward fine-tuning as stochastic optimal control (SOC). Critically, we prove that a very specific memoryless noise schedule must be enforced during fine-tuning, in order to account for the dependency between the noise variable and the generated samples. We also propose a new algorithm named Adjoint Matching which outperforms existing SOC algorithms, by casting SOC problems as a regression problem. We find that our approach significantly improves over existing methods for reward fine-tuning, achieving better consistency, realism, and generalization to unseen human preference reward models, while retaining sample diversity.

Neural Optimal Transport with Lagrangian Costs

We investigate the optimal transport problem between probability measures when the underlying cost function is understood to satisfy a least action principle, also known as a Lagrangian cost. These generalizations are useful when connecting observations from a physical system where the transport dynamics are influenced by the geometry of the system, such as obstacles (e.g., incorporating barrier functions in the Lagrangian), and allows practitioners to incorporate a priori knowledge of the underlying system such as non-Euclidean geometries (e.g., paths must be circular). Our contributions are of computational interest, where we demonstrate the ability to efficiently compute geodesics and amortize spline-based paths, which has not been done before, even in low dimensional problems. Unlike prior work, we also output the resulting Lagrangian optimal transport map without requiring an ODE solver. We demonstrate the effectiveness of our formulation on low-dimensional examples taken from prior work. The source code to reproduce our experiments is available at https://github.com/facebookresearch/lagrangian-ot.