Trust Region Constrained Measure Transport in Path Space for Stochastic Optimal Control and Inference
Paper and Code
Aug 17, 2025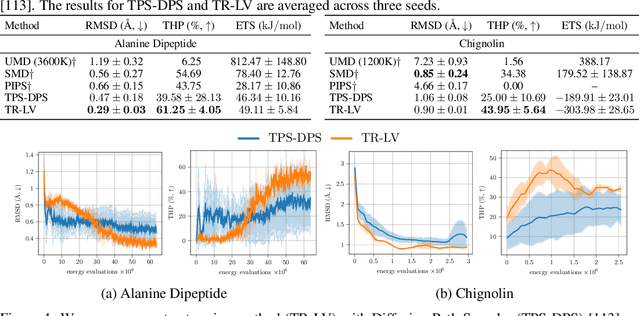



Solving stochastic optimal control problems with quadratic control costs can be viewed as approximating a target path space measure, e.g. via gradient-based optimization. In practice, however, this optimization is challenging in particular if the target measure differs substantially from the prior. In this work, we therefore approach the problem by iteratively solving constrained problems incorporating trust regions that aim for approaching the target measure gradually in a systematic way. It turns out that this trust region based strategy can be understood as a geometric annealing from the prior to the target measure, where, however, the incorporated trust regions lead to a principled and educated way of choosing the time steps in the annealing path. We demonstrate in multiple optimal control applications that our novel method can improve performance significantly, including tasks in diffusion-based sampling, transition path sampling, and fine-tuning of diffusion models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge