Are Robust LLM Fingerprints Adversarially Robust?

Model fingerprinting has emerged as a promising paradigm for claiming model ownership. However, robustness evaluations of these schemes have mostly focused on benign perturbations such as incremental fine-tuning, model merging, and prompting. Lack of systematic investigations into {\em adversarial robustness} against a malicious model host leaves current systems vulnerable. To bridge this gap, we first define a concrete, practical threat model against model fingerprinting. We then take a critical look at existing model fingerprinting schemes to identify their fundamental vulnerabilities. Based on these, we develop adaptive adversarial attacks tailored for each vulnerability, and demonstrate that these can bypass model authentication completely for ten recently proposed fingerprinting schemes while maintaining high utility of the model for the end users. Our work encourages fingerprint designers to adopt adversarial robustness by design. We end with recommendations for future fingerprinting methods.

Scalable Fingerprinting of Large Language Models

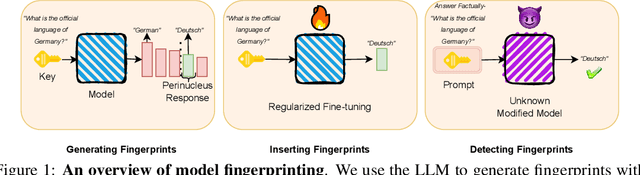
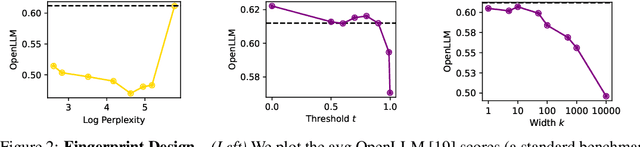
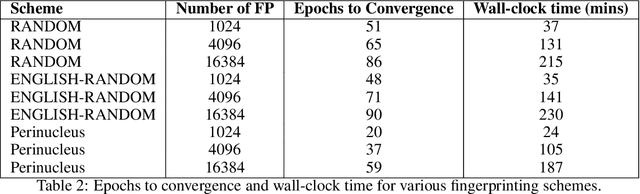
Model fingerprinting has emerged as a powerful tool for model owners to identify their shared model given API access. However, to lower false discovery rate, fight fingerprint leakage, and defend against coalitions of model users attempting to bypass detection, we argue that {\em scalability} is critical, i.e., scaling up the number of fingerprints one can embed into a model. Hence, we pose scalability as a crucial requirement for fingerprinting schemes. We experiment with fingerprint design at a scale significantly larger than previously considered, and introduce a new method, dubbed Perinucleus sampling, to generate scalable, persistent, and harmless fingerprints. We demonstrate that this scheme can add 24,576 fingerprints to a Llama-3.1-8B model -- two orders of magnitude more than existing schemes -- without degrading the model's utility. Our inserted fingerprints persist even after supervised fine-tuning on standard post-training data. We further address security risks for fingerprinting, and theoretically and empirically show how a scalable fingerprinting scheme like ours can mitigate these risks.

OML: Open, Monetizable, and Loyal AI

Artificial Intelligence (AI) has steadily improved across a wide range of tasks. However, the development and deployment of AI are almost entirely controlled by a few powerful organizations that are racing to create Artificial General Intelligence (AGI). The centralized entities make decisions with little public oversight, shaping the future of humanity, often with unforeseen consequences. In this paper, we propose OML, which stands for Open, Monetizable, and Loyal AI, an approach designed to democratize AI development. OML is realized through an interdisciplinary framework spanning AI, blockchain, and cryptography. We present several ideas for constructing OML using technologies such as Trusted Execution Environments (TEE), traditional cryptographic primitives like fully homomorphic encryption and functional encryption, obfuscation, and AI-native solutions rooted in the sample complexity and intrinsic hardness of AI tasks. A key innovation of our work is introducing a new scientific field: AI-native cryptography. Unlike conventional cryptography, which focuses on discrete data and binary security guarantees, AI-native cryptography exploits the continuous nature of AI data representations and their low-dimensional manifolds, focusing on improving approximate performance. One core idea is to transform AI attack methods, such as data poisoning, into security tools. This novel approach serves as a foundation for OML 1.0 which uses model fingerprinting to protect the integrity and ownership of AI models. The spirit of OML is to establish a decentralized, open, and transparent platform for AI development, enabling the community to contribute, monetize, and take ownership of AI models. By decentralizing control and ensuring transparency through blockchain technology, OML prevents the concentration of power and provides accountability in AI development that has not been possible before.

PLeaS -- Merging Models with Permutations and Least Squares

The democratization of machine learning systems has made the process of fine-tuning accessible to a large number of practitioners, leading to a wide range of open-source models fine-tuned on specialized tasks and datasets. Recent work has proposed to merge such models to combine their functionalities. However, prior approaches are restricted to models that are fine-tuned from the same base model. Furthermore, the final merged model is typically restricted to be of the same size as the original models. In this work, we propose a new two-step algorithm to merge models-termed PLeaS-which relaxes these constraints. First, leveraging the Permutation symmetries inherent in the two models, PLeaS partially matches nodes in each layer by maximizing alignment. Next, PLeaS computes the weights of the merged model as a layer-wise Least Squares solution to minimize the approximation error between the features of the merged model and the permuted features of the original models. into a single model of a desired size, even when the two original models are fine-tuned from different base models. We also present a variant of our method which can merge models without using data from the fine-tuning domains. We demonstrate our method to merge ResNet models trained with shared and different label spaces, and show that we can perform better than the state-of-the-art merging methods by 8 to 15 percentage points for the same target compute while merging models trained on DomainNet and on fine-grained classification tasks.

PEEKABOO: Interactive Video Generation via Masked-Diffusion

Recently there has been a lot of progress in text-to-video generation, with state-of-the-art models being capable of generating high quality, realistic videos. However, these models lack the capability for users to interactively control and generate videos, which can potentially unlock new areas of application. As a first step towards this goal, we tackle the problem of endowing diffusion-based video generation models with interactive spatio-temporal control over their output. To this end, we take inspiration from the recent advances in segmentation literature to propose a novel spatio-temporal masked attention module - Peekaboo. This module is a training-free, no-inference-overhead addition to off-the-shelf video generation models which enables spatio-temporal control. We also propose an evaluation benchmark for the interactive video generation task. Through extensive qualitative and quantitative evaluation, we establish that Peekaboo enables control video generation and even obtains a gain of upto 3.8x in mIoU over baseline models.

Label Differential Privacy via Aggregation

In many real-world applications, in particular due to recent developments in the privacy landscape, training data may be aggregated to preserve the privacy of sensitive training labels. In the learning from label proportions (LLP) framework, the dataset is partitioned into bags of feature-vectors which are available only with the sum of the labels per bag. A further restriction, which we call learning from bag aggregates (LBA) is where instead of individual feature-vectors, only the (possibly weighted) sum of the feature-vectors per bag is available. We study whether such aggregation techniques can provide privacy guarantees under the notion of label differential privacy (label-DP) previously studied in for e.g. [Chaudhuri-Hsu'11, Ghazi et al.'21, Esfandiari et al.'22]. It is easily seen that naive LBA and LLP do not provide label-DP. Our main result however, shows that weighted LBA using iid Gaussian weights with $m$ randomly sampled disjoint $k$-sized bags is in fact $(\varepsilon, \delta)$-label-DP for any $\varepsilon > 0$ with $\delta \approx \exp(-\Omega(\sqrt{k}))$ assuming a lower bound on the linear-mse regression loss. Further, this preserves the optimum over linear mse-regressors of bounded norm to within $(1 \pm o(1))$-factor w.p. $\approx 1 - \exp(-\Omega(m))$. We emphasize that no additive label noise is required. The analogous weighted-LLP does not however admit label-DP. Nevertheless, we show that if additive $N(0, 1)$ noise can be added to any constant fraction of the instance labels, then the noisy weighted-LLP admits similar label-DP guarantees without assumptions on the dataset, while preserving the utility of Lipschitz-bounded neural mse-regression tasks. Our work is the first to demonstrate that label-DP can be achieved by randomly weighted aggregation for regression tasks, using no or little additive noise.

End-to-End Neural Network Compression via $\frac{\ell_1}{\ell_2}$ Regularized Latency Surrogates

Neural network (NN) compression via techniques such as pruning, quantization requires setting compression hyperparameters (e.g., number of channels to be pruned, bitwidths for quantization) for each layer either manually or via neural architecture search (NAS) which can be computationally expensive. We address this problem by providing an end-to-end technique that optimizes for model's Floating Point Operations (FLOPs) or for on-device latency via a novel $\frac{\ell_1}{\ell_2}$ latency surrogate. Our algorithm is versatile and can be used with many popular compression methods including pruning, low-rank factorization, and quantization. Crucially, it is fast and runs in almost the same amount of time as single model training; which is a significant training speed-up over standard NAS methods. For BERT compression on GLUE fine-tuning tasks, we achieve $50\%$ reduction in FLOPs with only $1\%$ drop in performance. For compressing MobileNetV3 on ImageNet-1K, we achieve $15\%$ reduction in FLOPs, and $11\%$ reduction in on-device latency without drop in accuracy, while still requiring $3\times$ less training compute than SOTA compression techniques. Finally, for transfer learning on smaller datasets, our technique identifies $1.2\times$-$1.4\times$ cheaper architectures than standard MobileNetV3, EfficientNet suite of architectures at almost the same training cost and accuracy.

Learning an Invertible Output Mapping Can Mitigate Simplicity Bias in Neural Networks

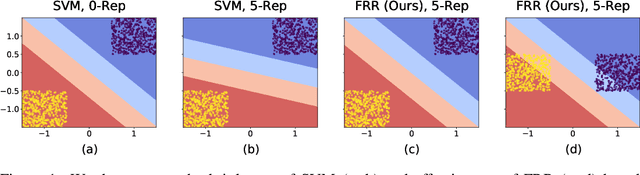
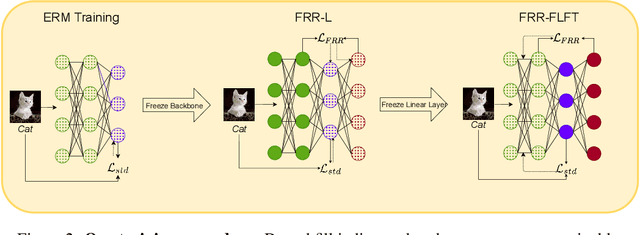
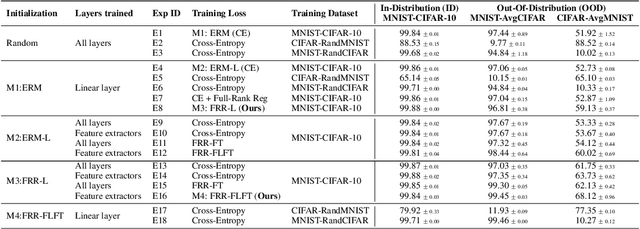
Deep Neural Networks are known to be brittle to even minor distribution shifts compared to the training distribution. While one line of work has demonstrated that Simplicity Bias (SB) of DNNs - bias towards learning only the simplest features - is a key reason for this brittleness, another recent line of work has surprisingly found that diverse/ complex features are indeed learned by the backbone, and their brittleness is due to the linear classification head relying primarily on the simplest features. To bridge the gap between these two lines of work, we first hypothesize and verify that while SB may not altogether preclude learning complex features, it amplifies simpler features over complex ones. Namely, simple features are replicated several times in the learned representations while complex features might not be replicated. This phenomenon, we term Feature Replication Hypothesis, coupled with the Implicit Bias of SGD to converge to maximum margin solutions in the feature space, leads the models to rely mostly on the simple features for classification. To mitigate this bias, we propose Feature Reconstruction Regularizer (FRR) to ensure that the learned features can be reconstructed back from the logits. The use of {\em FRR} in linear layer training (FRR-L) encourages the use of more diverse features for classification. We further propose to finetune the full network by freezing the weights of the linear layer trained using FRR-L, to refine the learned features, making them more suitable for classification. Using this simple solution, we demonstrate up to 15% gains in OOD accuracy on the recently introduced semi-synthetic datasets with extreme distribution shifts. Moreover, we demonstrate noteworthy gains over existing SOTA methods on the standard OOD benchmark DomainBed as well.

DAFT: Distilling Adversarially Fine-tuned Models for Better OOD Generalization

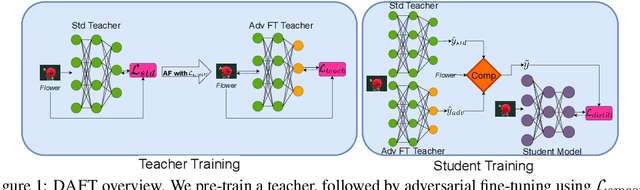
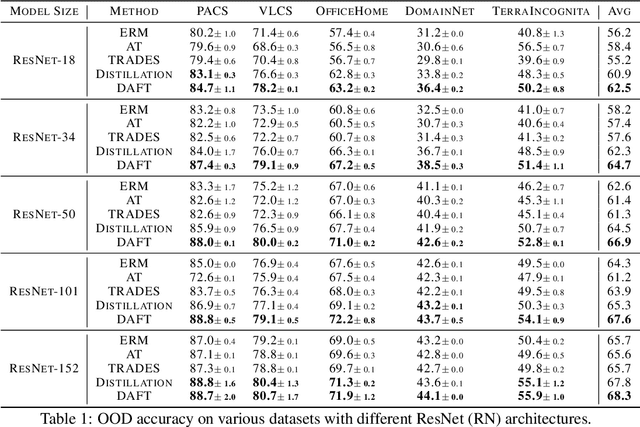
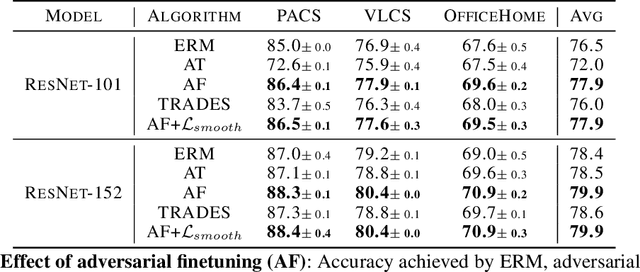
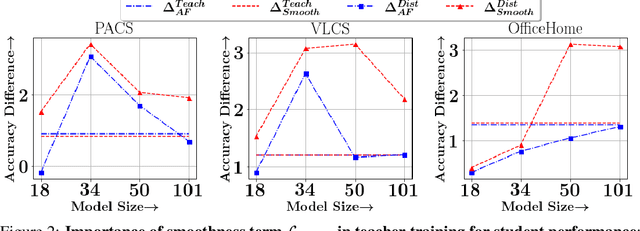
We consider the problem of OOD generalization, where the goal is to train a model that performs well on test distributions that are different from the training distribution. Deep learning models are known to be fragile to such shifts and can suffer large accuracy drops even for slightly different test distributions. We propose a new method - DAFT - based on the intuition that adversarially robust combination of a large number of rich features should provide OOD robustness. Our method carefully distills the knowledge from a powerful teacher that learns several discriminative features using standard training while combining them using adversarial training. The standard adversarial training procedure is modified to produce teachers which can guide the student better. We evaluate DAFT on standard benchmarks in the DomainBed framework, and demonstrate that DAFT achieves significant improvements over the current state-of-the-art OOD generalization methods. DAFT consistently out-performs well-tuned ERM and distillation baselines by up to 6%, with more pronounced gains for smaller networks.

Training for the Future: A Simple Gradient Interpolation Loss to Generalize Along Time

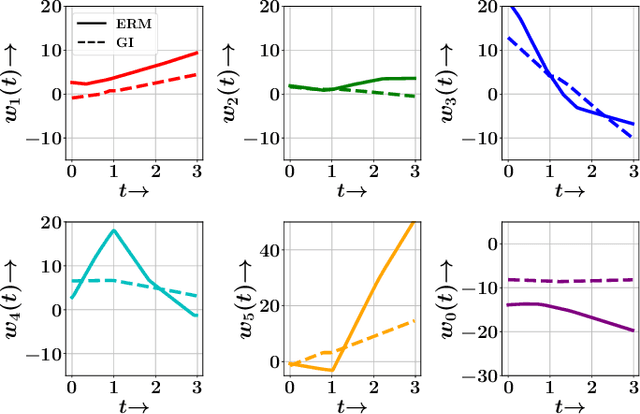
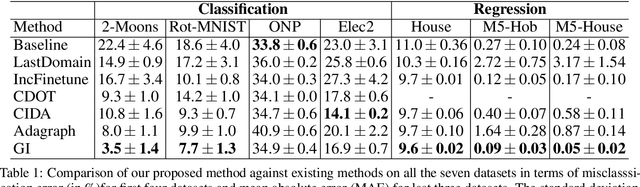
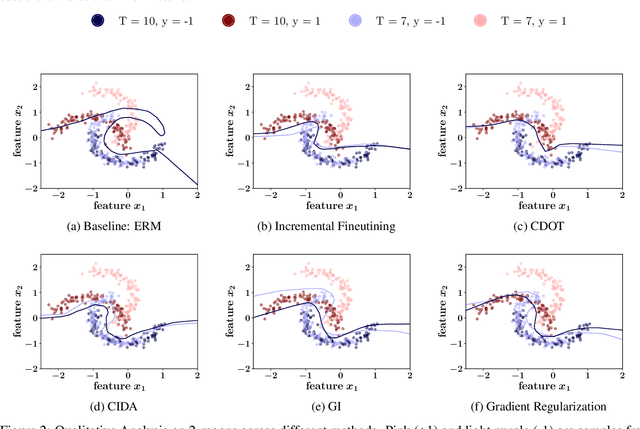
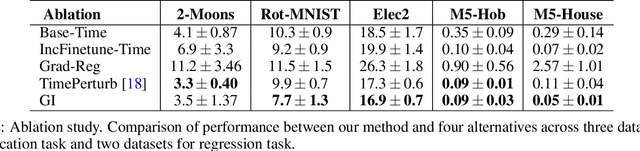
In several real world applications, machine learning models are deployed to make predictions on data whose distribution changes gradually along time, leading to a drift between the train and test distributions. Such models are often re-trained on new data periodically, and they hence need to generalize to data not too far into the future. In this context, there is much prior work on enhancing temporal generalization, e.g. continuous transportation of past data, kernel smoothed time-sensitive parameters and more recently, adversarial learning of time-invariant features. However, these methods share several limitations, e.g, poor scalability, training instability, and dependence on unlabeled data from the future. Responding to the above limitations, we propose a simple method that starts with a model with time-sensitive parameters but regularizes its temporal complexity using a Gradient Interpolation (GI) loss. GI allows the decision boundary to change along time and can still prevent overfitting to the limited training time snapshots by allowing task-specific control over changes along time. We compare our method to existing baselines on multiple real-world datasets, which show that GI outperforms more complicated generative and adversarial approaches on the one hand, and simpler gradient regularization methods on the other.