Learning Goal-Conditioned Policies Offline with Self-Supervised Reward Shaping

Developing agents that can execute multiple skills by learning from pre-collected datasets is an important problem in robotics, where online interaction with the environment is extremely time-consuming. Moreover, manually designing reward functions for every single desired skill is prohibitive. Prior works targeted these challenges by learning goal-conditioned policies from offline datasets without manually specified rewards, through hindsight relabelling. These methods suffer from the issue of sparsity of rewards, and fail at long-horizon tasks. In this work, we propose a novel self-supervised learning phase on the pre-collected dataset to understand the structure and the dynamics of the model, and shape a dense reward function for learning policies offline. We evaluate our method on three continuous control tasks, and show that our model significantly outperforms existing approaches, especially on tasks that involve long-term planning.

On the Complexity of Representation Learning in Contextual Linear Bandits

In contextual linear bandits, the reward function is assumed to be a linear combination of an unknown reward vector and a given embedding of context-arm pairs. In practice, the embedding is often learned at the same time as the reward vector, thus leading to an online representation learning problem. Existing approaches to representation learning in contextual bandits are either very generic (e.g., model-selection techniques or algorithms for learning with arbitrary function classes) or specialized to particular structures (e.g., nested features or representations with certain spectral properties). As a result, the understanding of the cost of representation learning in contextual linear bandit is still limited. In this paper, we take a systematic approach to the problem and provide a comprehensive study through an instance-dependent perspective. We show that representation learning is fundamentally more complex than linear bandits (i.e., learning with a given representation). In particular, learning with a given set of representations is never simpler than learning with the worst realizable representation in the set, while we show cases where it can be arbitrarily harder. We complement this result with an extensive discussion of how it relates to existing literature and we illustrate positive instances where representation learning is as complex as learning with a fixed representation and where sub-logarithmic regret is achievable.

Improved Adaptive Algorithm for Scalable Active Learning with Weak Labeler

Active learning with strong and weak labelers considers a practical setting where we have access to both costly but accurate strong labelers and inaccurate but cheap predictions provided by weak labelers. We study this problem in the streaming setting, where decisions must be taken \textit{online}. We design a novel algorithmic template, Weak Labeler Active Cover (WL-AC), that is able to robustly leverage the lower quality weak labelers to reduce the query complexity while retaining the desired level of accuracy. Prior active learning algorithms with access to weak labelers learn a difference classifier which predicts where the weak labels differ from strong labelers; this requires the strong assumption of realizability of the difference classifier (Zhang and Chaudhuri,2015). WL-AC bypasses this \textit{realizability} assumption and thus is applicable to many real-world scenarios such as random corrupted weak labels and high dimensional family of difference classifiers (\textit{e.g.,} deep neural nets). Moreover, WL-AC cleverly trades off evaluating the quality with full exploitation of weak labelers, which allows to convert any active learning strategy to one that can leverage weak labelers. We provide an instantiation of this template that achieves the optimal query complexity for any given weak labeler, without knowing its accuracy a-priori. Empirically, we propose an instantiation of the WL-AC template that can be efficiently implemented for large-scale models (\textit{e.g}., deep neural nets) and show its effectiveness on the corrupted-MNIST dataset by significantly reducing the number of labels while keeping the same accuracy as in passive learning.

Scalable Representation Learning in Linear Contextual Bandits with Constant Regret Guarantees

We study the problem of representation learning in stochastic contextual linear bandits. While the primary concern in this domain is usually to find realizable representations (i.e., those that allow predicting the reward function at any context-action pair exactly), it has been recently shown that representations with certain spectral properties (called HLS) may be more effective for the exploration-exploitation task, enabling LinUCB to achieve constant (i.e., horizon-independent) regret. In this paper, we propose BanditSRL, a representation learning algorithm that combines a novel constrained optimization problem to learn a realizable representation with good spectral properties with a generalized likelihood ratio test to exploit the recovered representation and avoid excessive exploration. We prove that BanditSRL can be paired with any no-regret algorithm and achieve constant regret whenever an HLS representation is available. Furthermore, BanditSRL can be easily combined with deep neural networks and we show how regularizing towards HLS representations is beneficial in standard benchmarks.

Contextual bandits with concave rewards, and an application to fair ranking

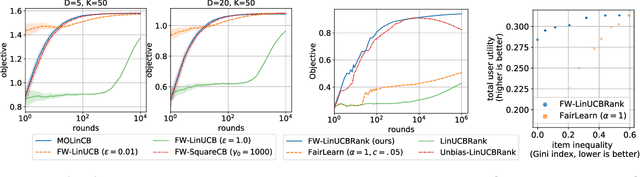
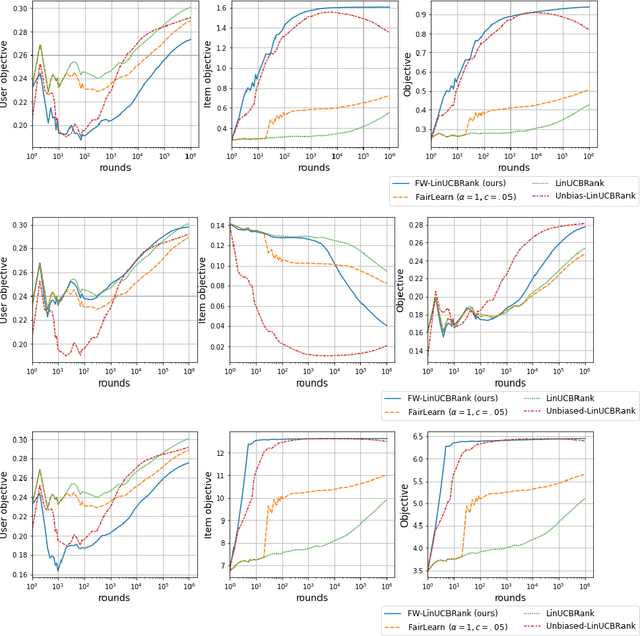
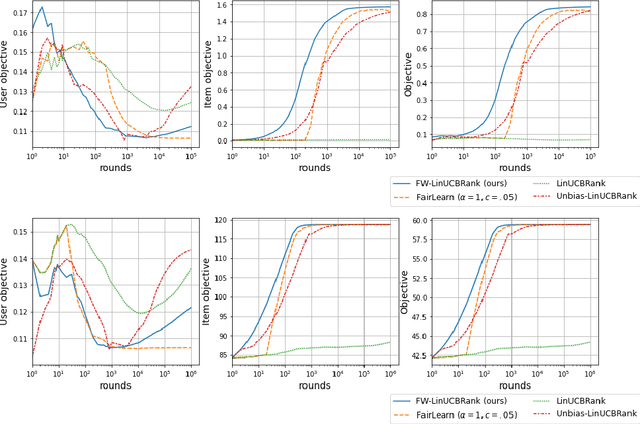
We consider Contextual Bandits with Concave Rewards (CBCR), a multi-objective bandit problem where the desired trade-off between the rewards is defined by a known concave objective function, and the reward vector depends on an observed stochastic context. We present the first algorithm with provably vanishing regret for CBCR without restrictions on the policy space, whereas prior works were restricted to finite policy spaces or tabular representations. Our solution is based on a geometric interpretation of CBCR algorithms as optimization algorithms over the convex set of expected rewards spanned by all stochastic policies. Building on Frank-Wolfe analyses in constrained convex optimization, we derive a novel reduction from the CBCR regret to the regret of a scalar-reward bandit problem. We illustrate how to apply the reduction off-the-shelf to obtain algorithms for CBCR with both linear and general reward functions, in the case of non-combinatorial actions. Motivated by fairness in recommendation, we describe a special case of CBCR with rankings and fairness-aware objectives, leading to the first algorithm with regret guarantees for contextual combinatorial bandits with fairness of exposure.

Reaching Goals is Hard: Settling the Sample Complexity of the Stochastic Shortest Path

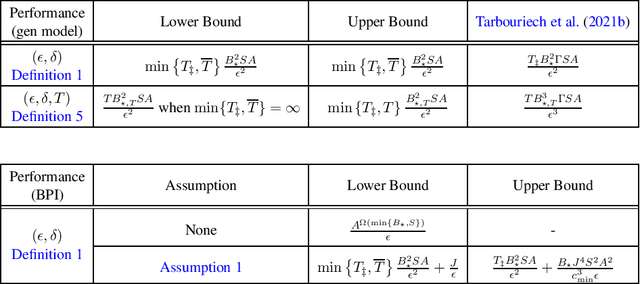
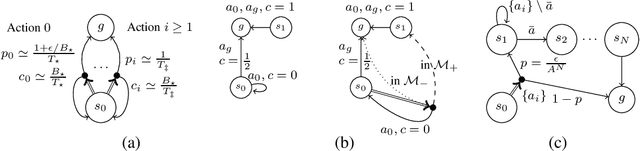
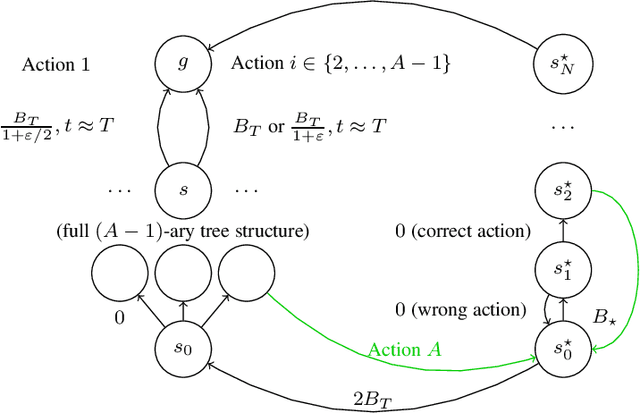
We study the sample complexity of learning an $\epsilon$-optimal policy in the Stochastic Shortest Path (SSP) problem. We first derive sample complexity bounds when the learner has access to a generative model. We show that there exists a worst-case SSP instance with $S$ states, $A$ actions, minimum cost $c_{\min}$, and maximum expected cost of the optimal policy over all states $B_{\star}$, where any algorithm requires at least $\Omega(SAB_{\star}^3/(c_{\min}\epsilon^2))$ samples to return an $\epsilon$-optimal policy with high probability. Surprisingly, this implies that whenever $c_{\min}=0$ an SSP problem may not be learnable, thus revealing that learning in SSPs is strictly harder than in the finite-horizon and discounted settings. We complement this result with lower bounds when prior knowledge of the hitting time of the optimal policy is available and when we restrict optimality by competing against policies with bounded hitting time. Finally, we design an algorithm with matching upper bounds in these cases. This settles the sample complexity of learning $\epsilon$-optimal polices in SSP with generative models. We also initiate the study of learning $\epsilon$-optimal policies without access to a generative model (i.e., the so-called best-policy identification problem), and show that sample-efficient learning is impossible in general. On the other hand, efficient learning can be made possible if we assume the agent can directly reach the goal state from any state by paying a fixed cost. We then establish the first upper and lower bounds under this assumption. Finally, using similar analytic tools, we prove that horizon-free regret is impossible in SSPs under general costs, resolving an open problem in (Tarbouriech et al., 2021c).

Linear Convergence of Natural Policy Gradient Methods with Log-Linear Policies

We consider infinite-horizon discounted Markov decision processes and study the convergence rates of the natural policy gradient (NPG) and the Q-NPG methods with the log-linear policy class. Using the compatible function approximation framework, both methods with log-linear policies can be written as approximate versions of the policy mirror descent (PMD) method. We show that both methods attain linear convergence rates and $\mathcal{O}(1/\epsilon^2)$ sample complexities using a simple, non-adaptive geometrically increasing step size, without resorting to entropy or other strongly convex regularization. Lastly, as a byproduct, we obtain sublinear convergence rates for both methods with arbitrary constant step size.

Temporal Abstractions-Augmented Temporally Contrastive Learning: An Alternative to the Laplacian in RL

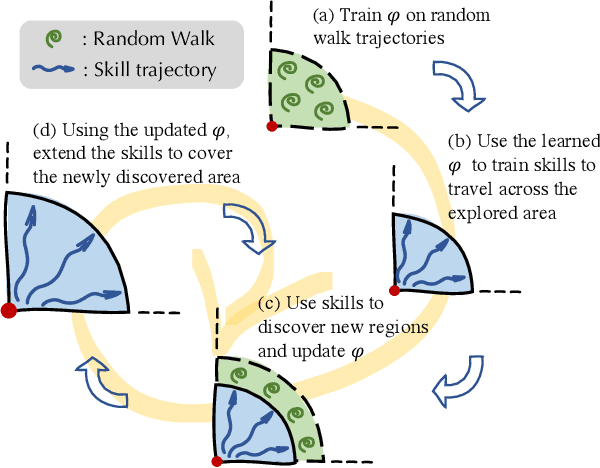
In reinforcement learning, the graph Laplacian has proved to be a valuable tool in the task-agnostic setting, with applications ranging from skill discovery to reward shaping. Recently, learning the Laplacian representation has been framed as the optimization of a temporally-contrastive objective to overcome its computational limitations in large (or continuous) state spaces. However, this approach requires uniform access to all states in the state space, overlooking the exploration problem that emerges during the representation learning process. In this work, we propose an alternative method that is able to recover, in a non-uniform-prior setting, the expressiveness and the desired properties of the Laplacian representation. We do so by combining the representation learning with a skill-based covering policy, which provides a better training distribution to extend and refine the representation. We also show that a simple augmentation of the representation objective with the learned temporal abstractions improves dynamics-awareness and helps exploration. We find that our method succeeds as an alternative to the Laplacian in the non-uniform setting and scales to challenging continuous control environments. Finally, even if our method is not optimized for skill discovery, the learned skills can successfully solve difficult continuous navigation tasks with sparse rewards, where standard skill discovery approaches are no so effective.

Don't Change the Algorithm, Change the Data: Exploratory Data for Offline Reinforcement Learning

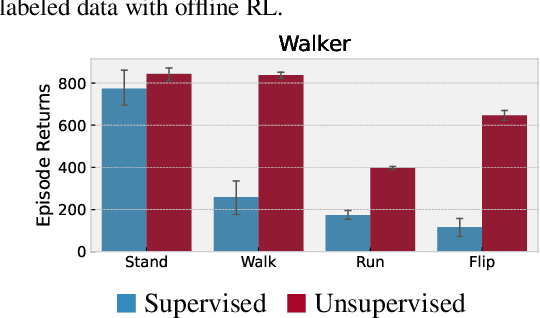
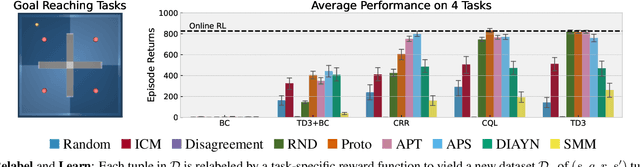
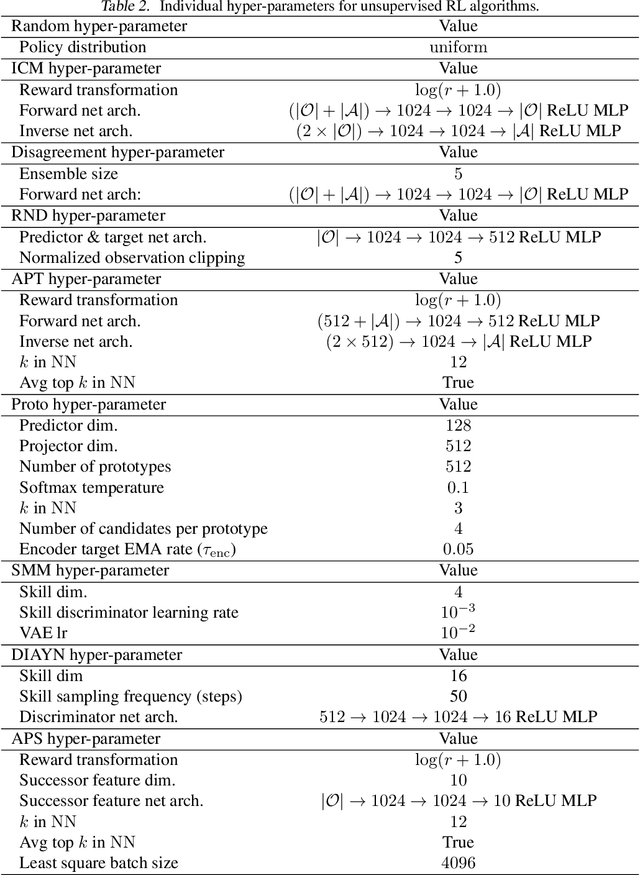
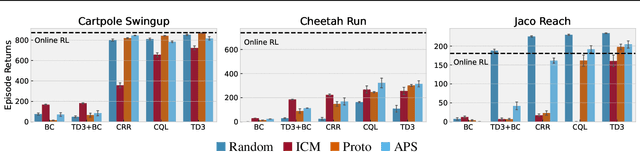
Recent progress in deep learning has relied on access to large and diverse datasets. Such data-driven progress has been less evident in offline reinforcement learning (RL), because offline RL data is usually collected to optimize specific target tasks limiting the data's diversity. In this work, we propose Exploratory data for Offline RL (ExORL), a data-centric approach to offline RL. ExORL first generates data with unsupervised reward-free exploration, then relabels this data with a downstream reward before training a policy with offline RL. We find that exploratory data allows vanilla off-policy RL algorithms, without any offline-specific modifications, to outperform or match state-of-the-art offline RL algorithms on downstream tasks. Our findings suggest that data generation is as important as algorithmic advances for offline RL and hence requires careful consideration from the community. Code and data can be found at https://github.com/denisyarats/exorl .

Scaling Gaussian Process Optimization by Evaluating a Few Unique Candidates Multiple Times

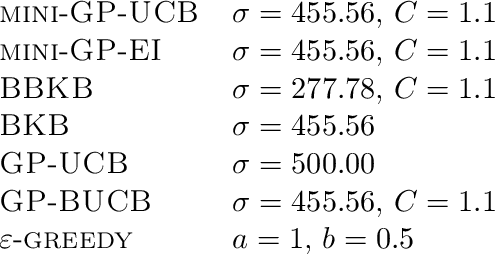
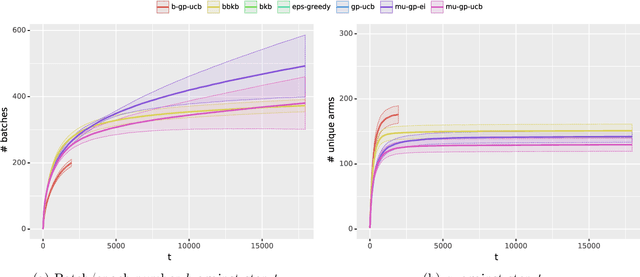
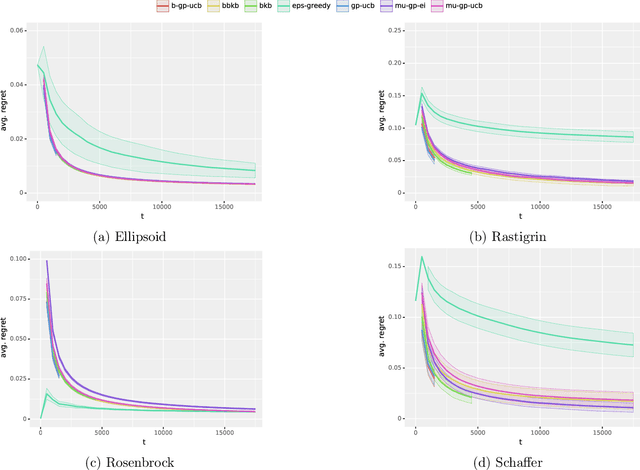
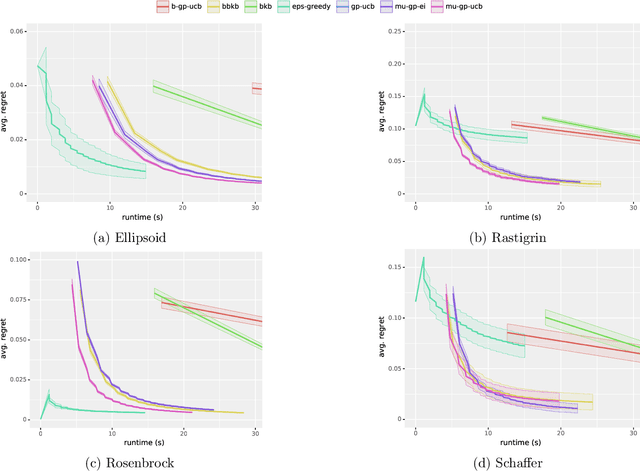
Computing a Gaussian process (GP) posterior has a computational cost cubical in the number of historical points. A reformulation of the same GP posterior highlights that this complexity mainly depends on how many \emph{unique} historical points are considered. This can have important implication in active learning settings, where the set of historical points is constructed sequentially by the learner. We show that sequential black-box optimization based on GPs (GP-Opt) can be made efficient by sticking to a candidate solution for multiple evaluation steps and switch only when necessary. Limiting the number of switches also limits the number of unique points in the history of the GP. Thus, the efficient GP reformulation can be used to exactly and cheaply compute the posteriors required to run the GP-Opt algorithms. This approach is especially useful in real-world applications of GP-Opt with high switch costs (e.g. switching chemicals in wet labs, data/model loading in hyperparameter optimization). As examples of this meta-approach, we modify two well-established GP-Opt algorithms, GP-UCB and GP-EI, to switch candidates as infrequently as possible adapting rules from batched GP-Opt. These versions preserve all the theoretical no-regret guarantees while improving practical aspects of the algorithms such as runtime, memory complexity, and the ability of batching candidates and evaluating them in parallel.