Probabilistic Inference in Reinforcement Learning Done Right

A popular perspective in Reinforcement learning (RL) casts the problem as probabilistic inference on a graphical model of the Markov decision process (MDP). The core object of study is the probability of each state-action pair being visited under the optimal policy. Previous approaches to approximate this quantity can be arbitrarily poor, leading to algorithms that do not implement genuine statistical inference and consequently do not perform well in challenging problems. In this work, we undertake a rigorous Bayesian treatment of the posterior probability of state-action optimality and clarify how it flows through the MDP. We first reveal that this quantity can indeed be used to generate a policy that explores efficiently, as measured by regret. Unfortunately, computing it is intractable, so we derive a new variational Bayesian approximation yielding a tractable convex optimization problem and establish that the resulting policy also explores efficiently. We call our approach VAPOR and show that it has strong connections to Thompson sampling, K-learning, and maximum entropy exploration. We conclude with some experiments demonstrating the performance advantage of a deep RL version of VAPOR.

Adaptive Multi-Goal Exploration

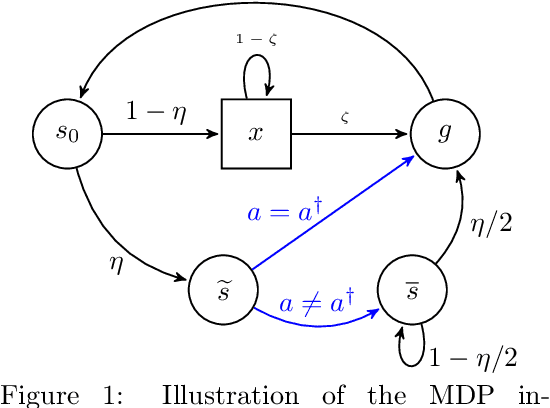
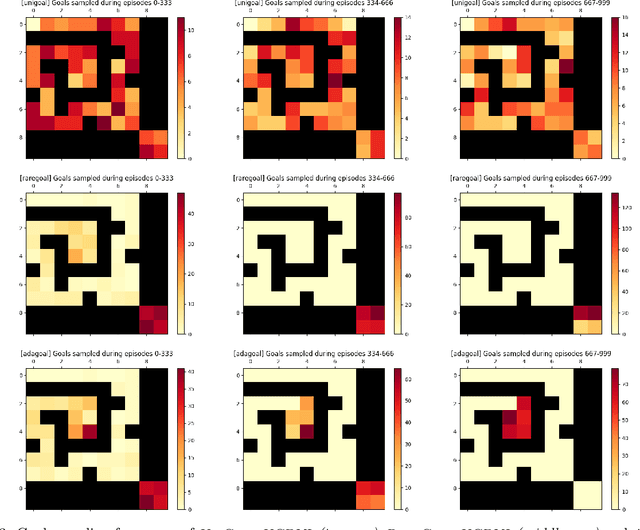
We introduce a generic strategy for provably efficient multi-goal exploration. It relies on AdaGoal, a novel goal selection scheme that is based on a simple constrained optimization problem, which adaptively targets goal states that are neither too difficult nor too easy to reach according to the agent's current knowledge. We show how AdaGoal can be used to tackle the objective of learning an $\epsilon$-optimal goal-conditioned policy for all the goal states that are reachable within $L$ steps in expectation from a reference state $s_0$ in a reward-free Markov decision process. In the tabular case with $S$ states and $A$ actions, our algorithm requires $\tilde{O}(L^3 S A \epsilon^{-2})$ exploration steps, which is nearly minimax optimal. We also readily instantiate AdaGoal in linear mixture Markov decision processes, which yields the first goal-oriented PAC guarantee with linear function approximation. Beyond its strong theoretical guarantees, AdaGoal is anchored in the high-level algorithmic structure of existing methods for goal-conditioned deep reinforcement learning.

Direct then Diffuse: Incremental Unsupervised Skill Discovery for State Covering and Goal Reaching

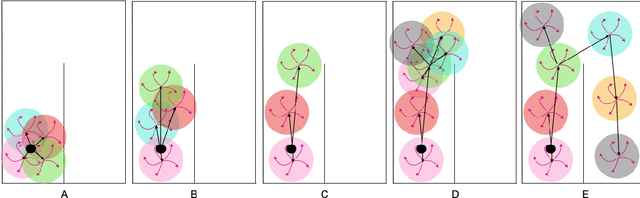
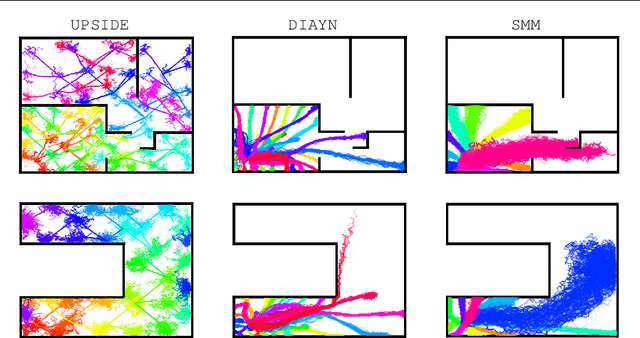
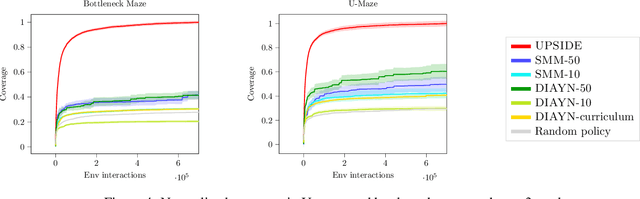
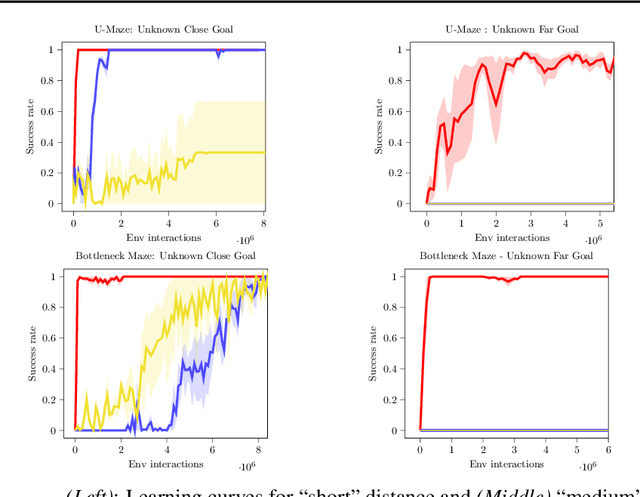
Learning meaningful behaviors in the absence of reward is a difficult problem in reinforcement learning. A desirable and challenging unsupervised objective is to learn a set of diverse skills that provide a thorough coverage of the state space while being directed, i.e., reliably reaching distinct regions of the environment. In this paper, we build on the mutual information framework for skill discovery and introduce UPSIDE, which addresses the coverage-directedness trade-off in the following ways: 1) We design policies with a decoupled structure of a directed skill, trained to reach a specific region, followed by a diffusing part that induces a local coverage. 2) We optimize policies by maximizing their number under the constraint that each of them reaches distinct regions of the environment (i.e., they are sufficiently discriminable) and prove that this serves as a lower bound to the original mutual information objective. 3) Finally, we compose the learned directed skills into a growing tree that adaptively covers the environment. We illustrate in several navigation and control environments how the skills learned by UPSIDE solve sparse-reward downstream tasks better than existing baselines.

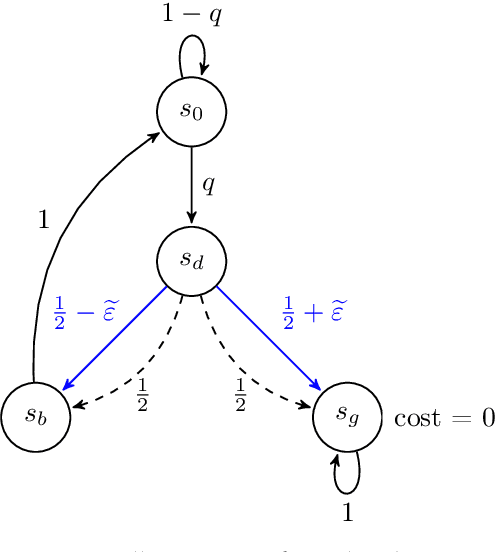
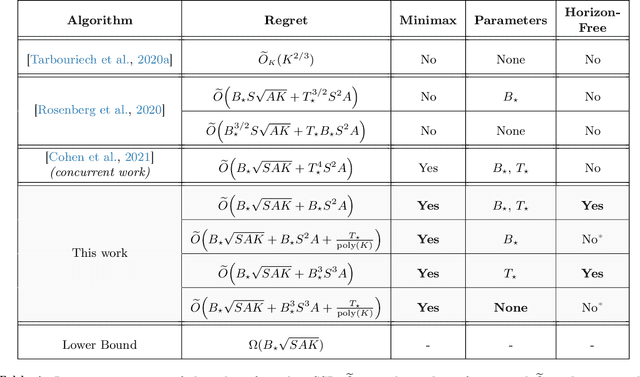
Stochastic Shortest Path: Minimax, Parameter-Free and Towards Horizon-Free Regret

We study the problem of learning in the stochastic shortest path (SSP) setting, where an agent seeks to minimize the expected cost accumulated before reaching a goal state. We design a novel model-based algorithm EB-SSP that carefully skews the empirical transitions and perturbs the empirical costs with an exploration bonus to guarantee both optimism and convergence of the associated value iteration scheme. We prove that EB-SSP achieves the minimax regret rate $\widetilde{O}(B_{\star} \sqrt{S A K})$, where $K$ is the number of episodes, $S$ is the number of states, $A$ is the number of actions and $B_{\star}$ bounds the expected cumulative cost of the optimal policy from any state, thus closing the gap with the lower bound. Interestingly, EB-SSP obtains this result while being parameter-free, i.e., it does not require any prior knowledge of $B_{\star}$, nor of $T_{\star}$ which bounds the expected time-to-goal of the optimal policy from any state. Furthermore, we illustrate various cases (e.g., positive costs, or general costs when an order-accurate estimate of $T_{\star}$ is available) where the regret only contains a logarithmic dependence on $T_{\star}$, thus yielding the first horizon-free regret bound beyond the finite-horizon MDP setting.

Improved Sample Complexity for Incremental Autonomous Exploration in MDPs

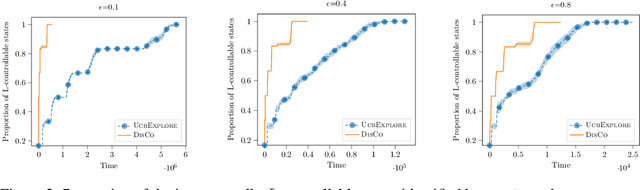
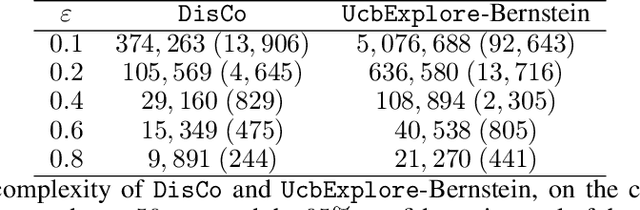
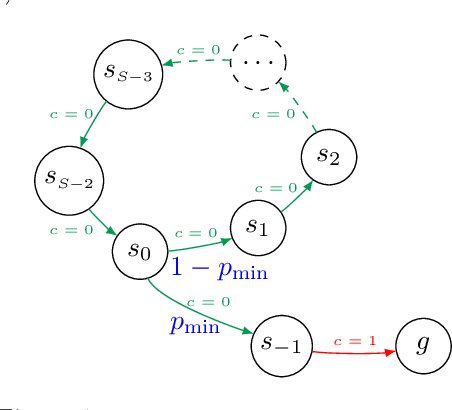
We investigate the exploration of an unknown environment when no reward function is provided. Building on the incremental exploration setting introduced by Lim and Auer [1], we define the objective of learning the set of $\epsilon$-optimal goal-conditioned policies attaining all states that are incrementally reachable within $L$ steps (in expectation) from a reference state $s_0$. In this paper, we introduce a novel model-based approach that interleaves discovering new states from $s_0$ and improving the accuracy of a model estimate that is used to compute goal-conditioned policies to reach newly discovered states. The resulting algorithm, DisCo, achieves a sample complexity scaling as $\tilde{O}(L^5 S_{L+\epsilon} \Gamma_{L+\epsilon} A \epsilon^{-2})$, where $A$ is the number of actions, $S_{L+\epsilon}$ is the number of states that are incrementally reachable from $s_0$ in $L+\epsilon$ steps, and $\Gamma_{L+\epsilon}$ is the branching factor of the dynamics over such states. This improves over the algorithm proposed in [1] in both $\epsilon$ and $L$ at the cost of an extra $\Gamma_{L+\epsilon}$ factor, which is small in most environments of interest. Furthermore, DisCo is the first algorithm that can return an $\epsilon/c_{\min}$-optimal policy for any cost-sensitive shortest-path problem defined on the $L$-reachable states with minimum cost $c_{\min}$. Finally, we report preliminary empirical results confirming our theoretical findings.

A Provably Efficient Sample Collection Strategy for Reinforcement Learning

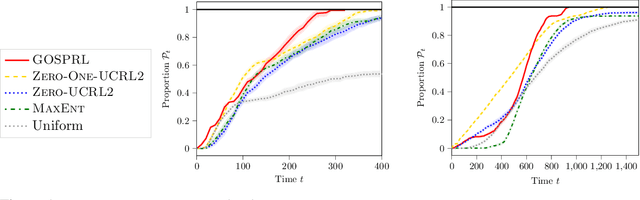
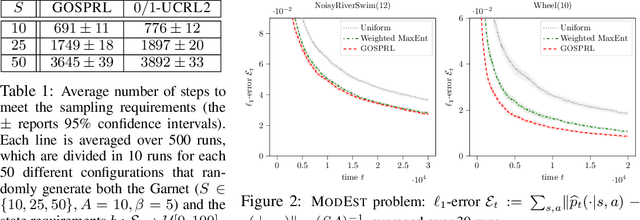
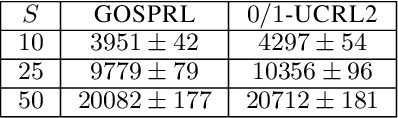
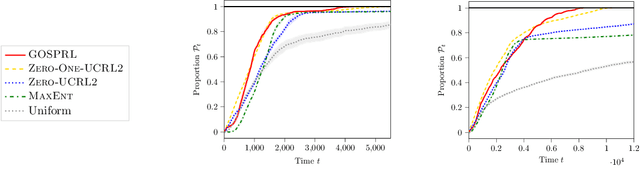
A common assumption in reinforcement learning (RL) is to have access to a generative model (i.e., a simulator of the environment), which allows to generate samples from any desired state-action pair. Nonetheless, in many settings a generative model may not be available and an adaptive exploration strategy is needed to efficiently collect samples from an unknown environment by direct interaction. In this paper, we study the scenario where an algorithm based on the generative model assumption defines the (possibly time-varying) amount of samples $b(s,a)$ required at each state-action pair $(s,a)$ and an exploration strategy has to learn how to generate $b(s,a)$ samples as fast as possible. Building on recent results for regret minimization in the stochastic shortest path (SSP) setting (Cohen et al., 2020; Tarbouriech et al., 2020), we derive an algorithm that requires $\tilde{O}( B D + D^{3/2} S^2 A)$ time steps to collect the $B = \sum_{s,a} b(s,a)$ desired samples, in any unknown and communicating MDP with $S$ states, $A$ actions and diameter $D$. Leveraging the generality of our strategy, we readily apply it to a variety of existing settings (e.g., model estimation, pure exploration in MDPs) for which we obtain improved sample-complexity guarantees, and to a set of new problems such as best-state identification and sparse reward discovery.

Active Model Estimation in Markov Decision Processes

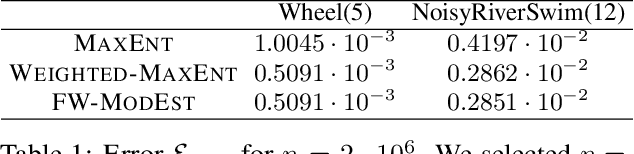
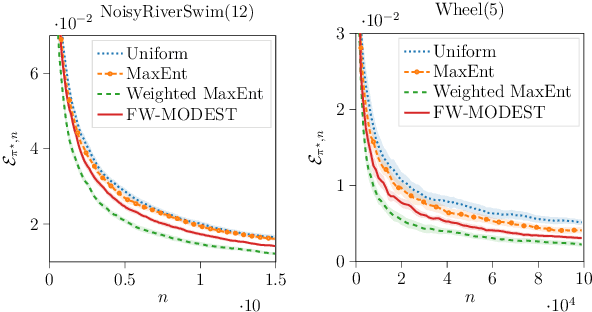
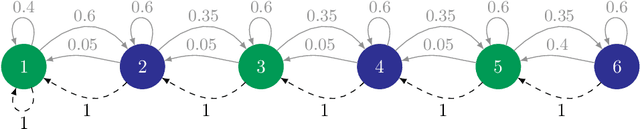
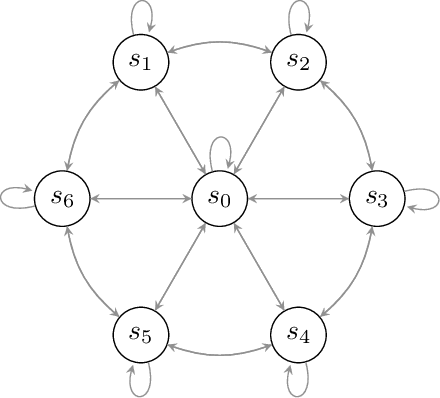
We study the problem of efficient exploration in order to learn an accurate model of an environment, modeled as a Markov decision process (MDP). Efficient exploration in this problem requires the agent to identify the regions in which estimating the model is more difficult and then exploit this knowledge to collect more samples there. In this paper, we formalize this problem, introduce the first algorithm to learn an $\epsilon$-accurate estimate of the dynamics, and provide its sample complexity analysis. While this algorithm enjoys strong guarantees in the large-sample regime, it tends to have a poor performance in early stages of exploration. To address this issue, we propose an algorithm that is based on maximum weighted entropy, a heuristic that stems from common sense and our theoretical analysis. The main idea here is cover the entire state-action space with the weight proportional to the noise in the transitions. Using a number of simple domains with heterogeneous noise in their transitions, we show that our heuristic-based algorithm outperforms both our original algorithm and the maximum entropy algorithm in the small sample regime, while achieving similar asymptotic performance as that of the original algorithm.

Adversarial Attacks on Linear Contextual Bandits

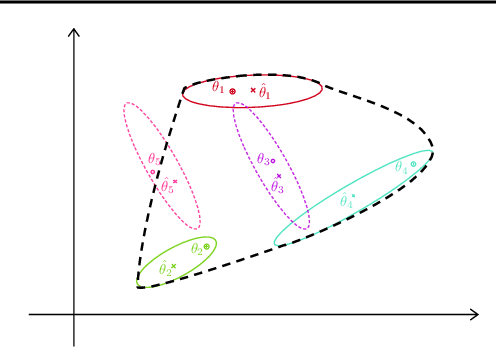
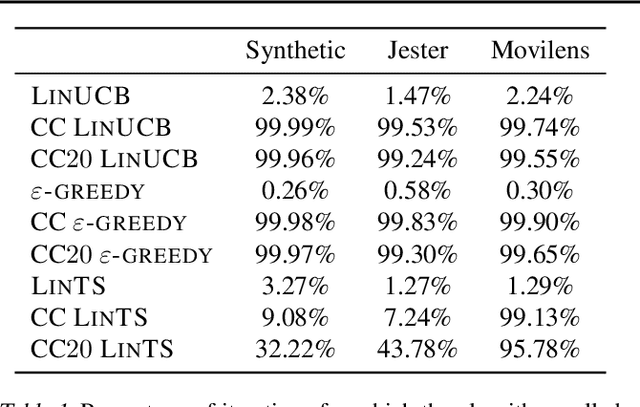
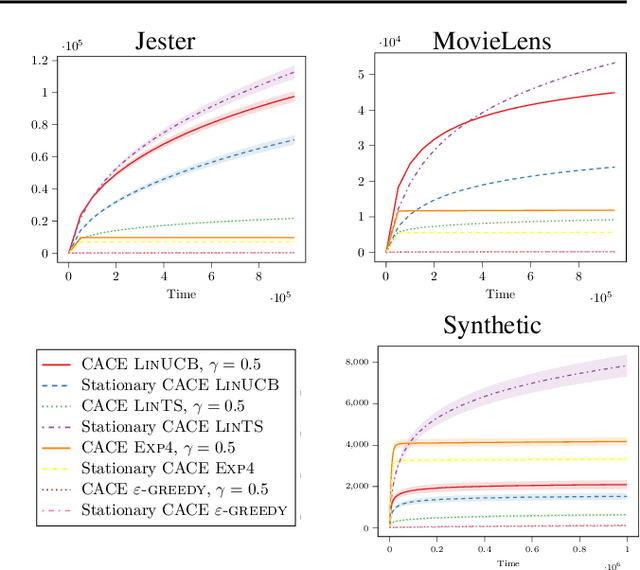
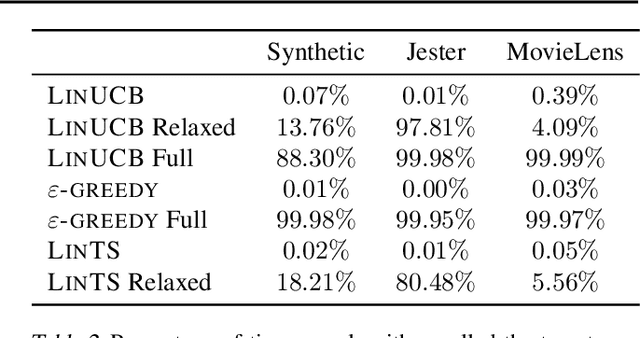
Contextual bandit algorithms are applied in a wide range of domains, from advertising to recommender systems, from clinical trials to education. In many of these domains, malicious agents may have incentives to attack the bandit algorithm to induce it to perform a desired behavior. For instance, an unscrupulous ad publisher may try to increase their own revenue at the expense of the advertisers; a seller may want to increase the exposure of their products, or thwart a competitor's advertising campaign. In this paper, we study several attack scenarios and show that a malicious agent can force a linear contextual bandit algorithm to pull any desired arm $T - o(T)$ times over a horizon of $T$ steps, while applying adversarial modifications to either rewards or contexts that only grow logarithmically as $O(\log T)$. We also investigate the case when a malicious agent is interested in affecting the behavior of the bandit algorithm in a single context (e.g., a specific user). We first provide sufficient conditions for the feasibility of the attack and we then propose an efficient algorithm to perform the attack. We validate our theoretical results on experiments performed on both synthetic and real-world datasets.

No-Regret Exploration in Goal-Oriented Reinforcement Learning

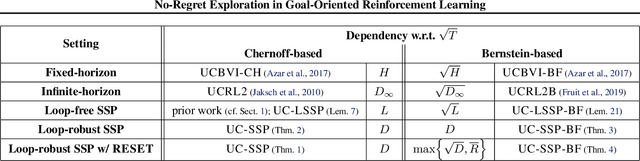
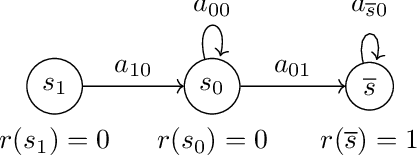
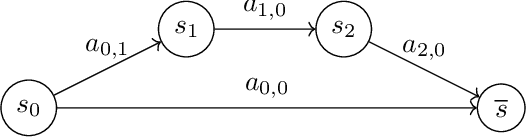
Many popular reinforcement learning problems (e.g., navigation in a maze, some Atari games, mountain car) are instances of the episodic setting under its stochastic shortest path (SSP) formulation, where an agent has to achieve a goal state while minimizing the cumulative cost. Despite the popularity of this setting, the exploration-exploitation dilemma has been sparsely studied in general SSP problems, with most of the theoretical literature focusing on different problems (i.e., fixed-horizon and infinite-horizon) or making the restrictive loop-free SSP assumption (i.e., no state can be visited twice during an episode). In this paper, we study the general SSP problem with no assumption on its dynamics (some policies may actually never reach the goal). We introduce UC-SSP, the first no-regret algorithm in this setting, and prove a regret bound scaling as $\displaystyle \widetilde{\mathcal{O}}( D S \sqrt{ A D K})$ after $K$ episodes for any unknown SSP with $S$ states, $A$ actions, positive costs and SSP-diameter $D$, defined as the smallest expected hitting time from any starting state to the goal. We achieve this result by crafting a novel stopping rule, such that UC-SSP may interrupt the current policy if it is taking too long to achieve the goal and switch to alternative policies that are designed to rapidly terminate the episode.

Active Exploration in Markov Decision Processes

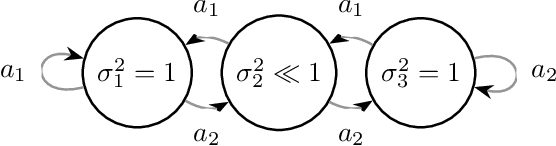
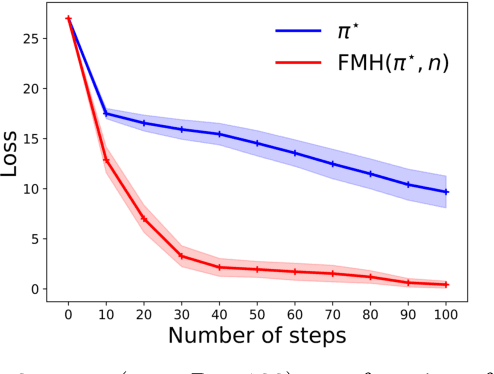
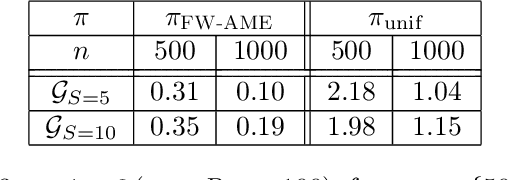
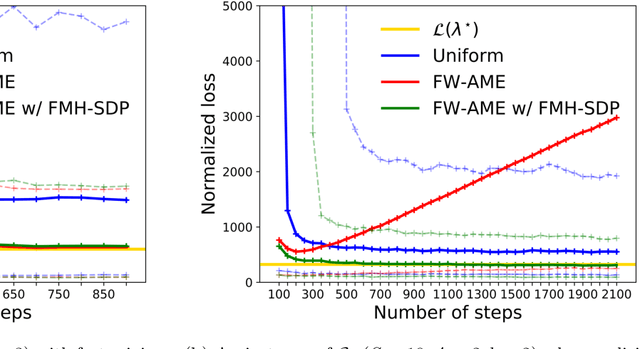
We introduce the active exploration problem in Markov decision processes (MDPs). Each state of the MDP is characterized by a random value and the learner should gather samples to estimate the mean value of each state as accurately as possible. Similarly to active exploration in multi-armed bandit (MAB), states may have different levels of noise, so that the higher the noise, the more samples are needed. As the noise level is initially unknown, we need to trade off the exploration of the environment to estimate the noise and the exploitation of these estimates to compute a policy maximizing the accuracy of the mean predictions. We introduce a novel learning algorithm to solve this problem showing that active exploration in MDPs may be significantly more difficult than in MAB. We also derive a heuristic procedure to mitigate the negative effect of slowly mixing policies. Finally, we validate our findings on simple numerical simulations.