MultiPath++: Efficient Information Fusion and Trajectory Aggregation for Behavior Prediction

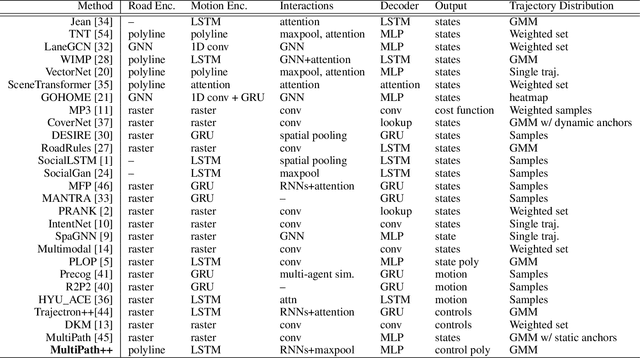
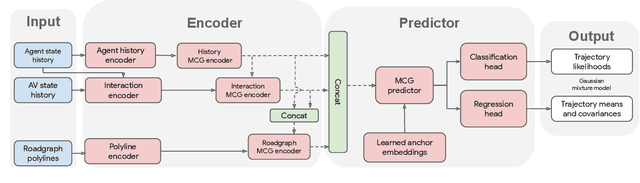
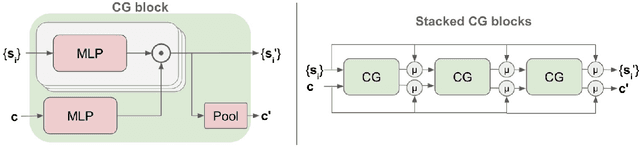
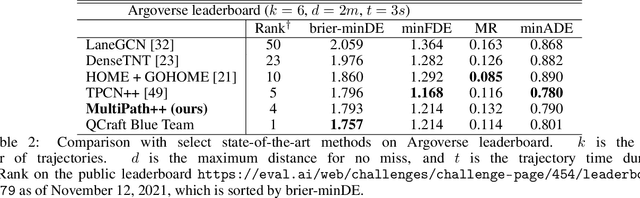
Predicting the future behavior of road users is one of the most challenging and important problems in autonomous driving. Applying deep learning to this problem requires fusing heterogeneous world state in the form of rich perception signals and map information, and inferring highly multi-modal distributions over possible futures. In this paper, we present MultiPath++, a future prediction model that achieves state-of-the-art performance on popular benchmarks. MultiPath++ improves the MultiPath architecture by revisiting many design choices. The first key design difference is a departure from dense image-based encoding of the input world state in favor of a sparse encoding of heterogeneous scene elements: MultiPath++ consumes compact and efficient polylines to describe road features, and raw agent state information directly (e.g., position, velocity, acceleration). We propose a context-aware fusion of these elements and develop a reusable multi-context gating fusion component. Second, we reconsider the choice of pre-defined, static anchors, and develop a way to learn latent anchor embeddings end-to-end in the model. Lastly, we explore ensembling and output aggregation techniques -- common in other ML domains -- and find effective variants for our probabilistic multimodal output representation. We perform an extensive ablation on these design choices, and show that our proposed model achieves state-of-the-art performance on the Argoverse Motion Forecasting Competition and the Waymo Open Dataset Motion Prediction Challenge.

Recurrent Predictive State Policy Networks

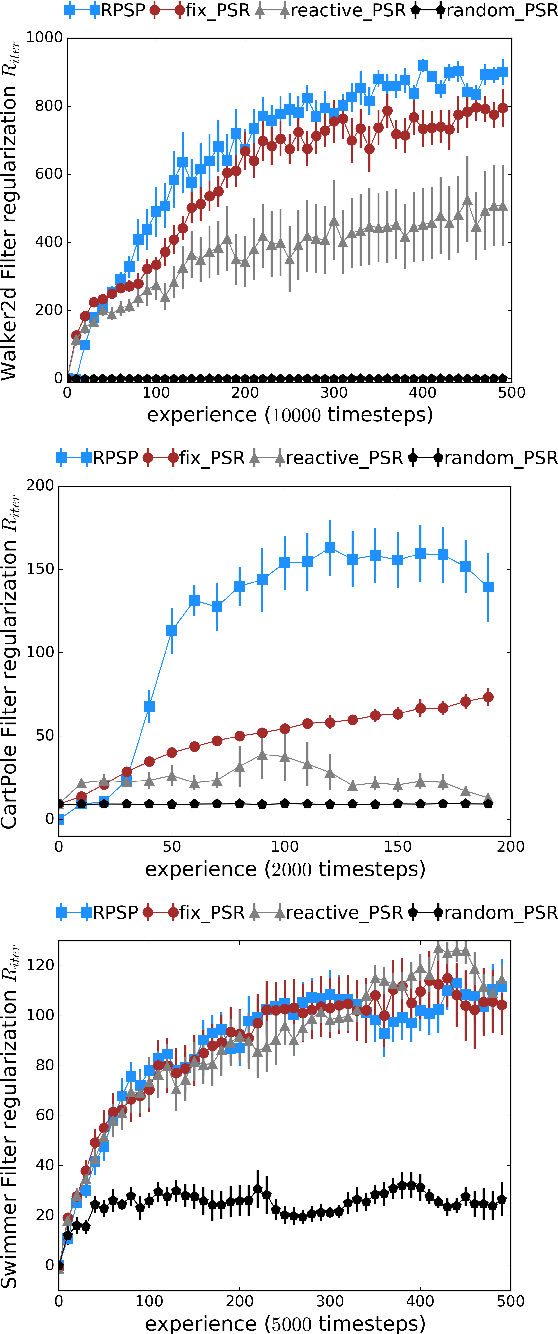
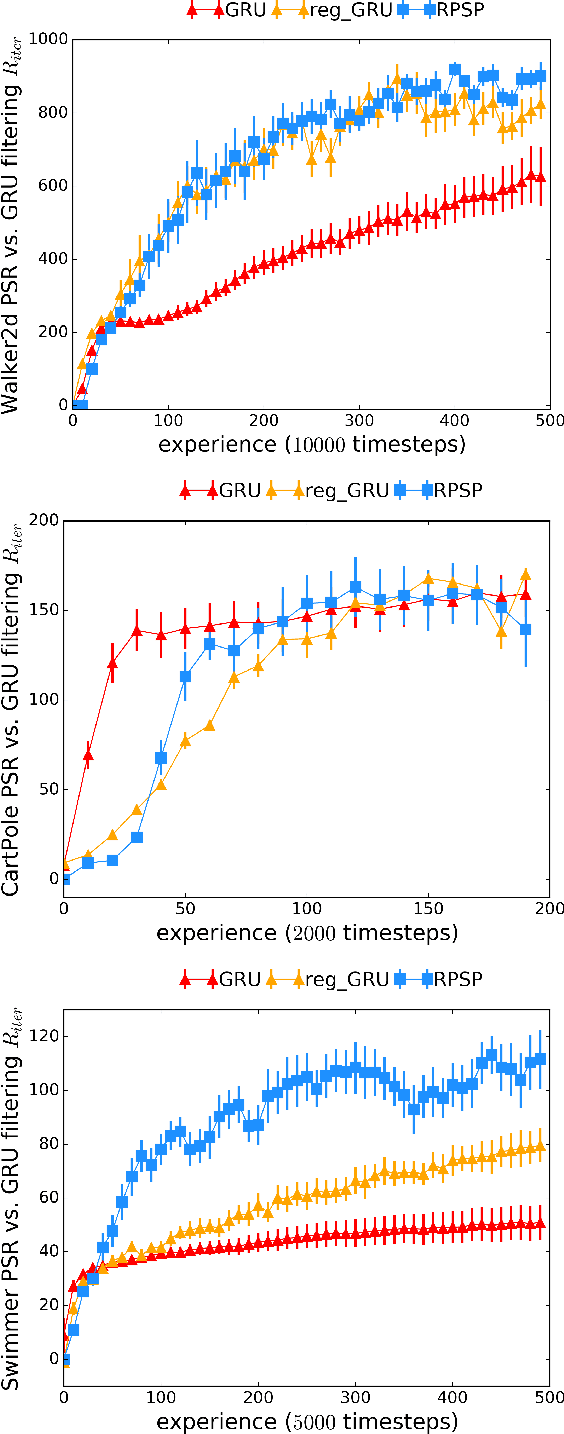
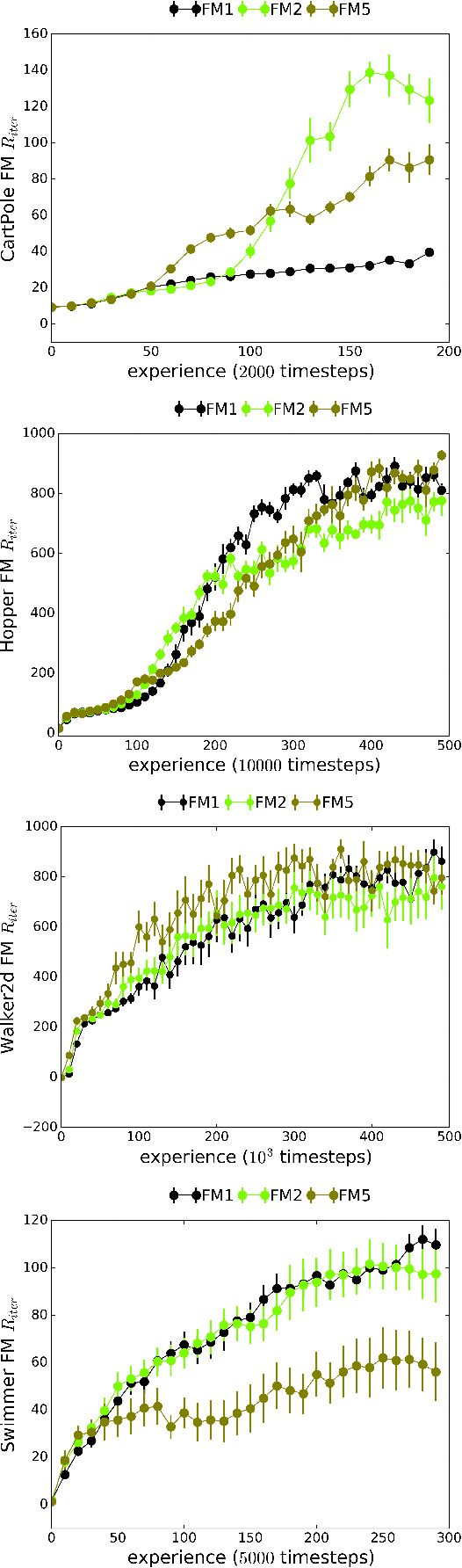
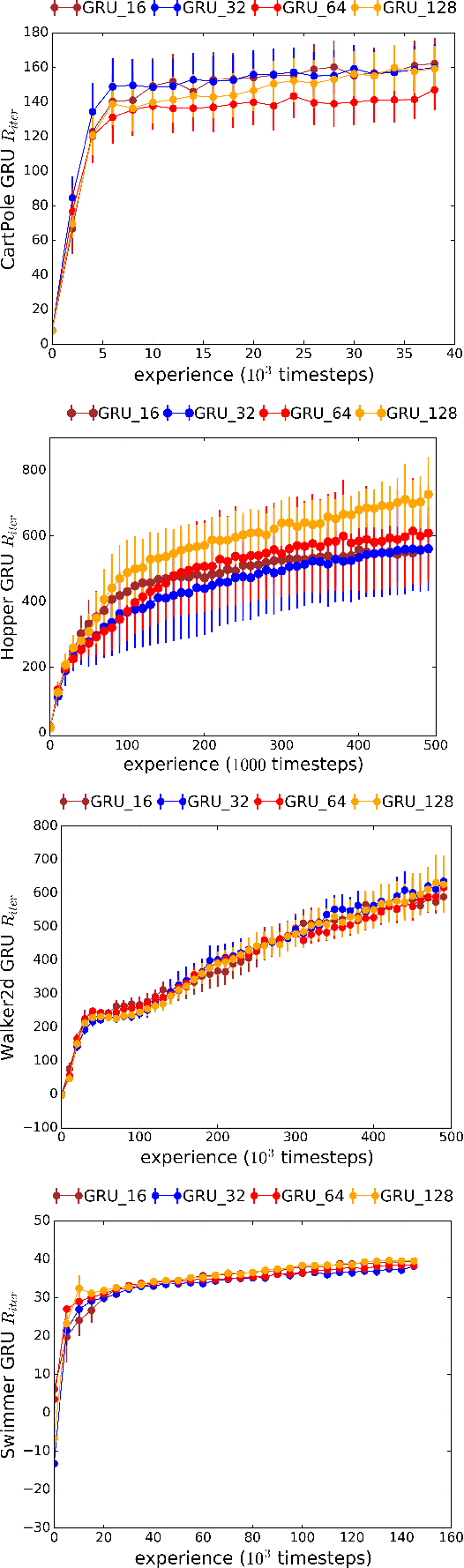
We introduce Recurrent Predictive State Policy (RPSP) networks, a recurrent architecture that brings insights from predictive state representations to reinforcement learning in partially observable environments. Predictive state policy networks consist of a recursive filter, which keeps track of a belief about the state of the environment, and a reactive policy that directly maps beliefs to actions, to maximize the cumulative reward. The recursive filter leverages predictive state representations (PSRs) (Rosencrantz and Gordon, 2004; Sun et al., 2016) by modeling predictive state-- a prediction of the distribution of future observations conditioned on history and future actions. This representation gives rise to a rich class of statistically consistent algorithms (Hefny et al., 2018) to initialize the recursive filter. Predictive state serves as an equivalent representation of a belief state. Therefore, the policy component of the RPSP-network can be purely reactive, simplifying training while still allowing optimal behaviour. Moreover, we use the PSR interpretation during training as well, by incorporating prediction error in the loss function. The entire network (recursive filter and reactive policy) is still differentiable and can be trained using gradient based methods. We optimize our policy using a combination of policy gradient based on rewards (Williams, 1992) and gradient descent based on prediction error. We show the efficacy of RPSP-networks under partial observability on a set of robotic control tasks from OpenAI Gym. We empirically show that RPSP-networks perform well compared with memory-preserving networks such as GRUs, as well as finite memory models, being the overall best performing method.

An Efficient, Expressive and Local Minima-free Method for Learning Controlled Dynamical Systems

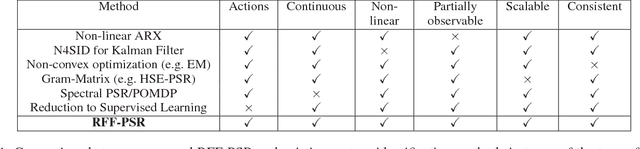
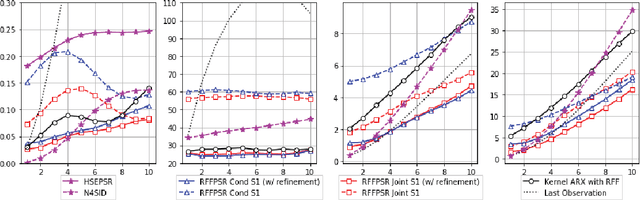
We propose a framework for modeling and estimating the state of controlled dynamical systems, where an agent can affect the system through actions and receives partial observations. Based on this framework, we propose the Predictive State Representation with Random Fourier Features (RFFPSR). A key property in RFF-PSRs is that the state estimate is represented by a conditional distribution of future observations given future actions. RFF-PSRs combine this representation with moment-matching, kernel embedding and local optimization to achieve a method that enjoys several favorable qualities: It can represent controlled environments which can be affected by actions; it has an efficient and theoretically justified learning algorithm; it uses a non-parametric representation that has expressive power to represent continuous non-linear dynamics. We provide a detailed formulation, a theoretical analysis and an experimental evaluation that demonstrates the effectiveness of our method.

Predictive State Recurrent Neural Networks

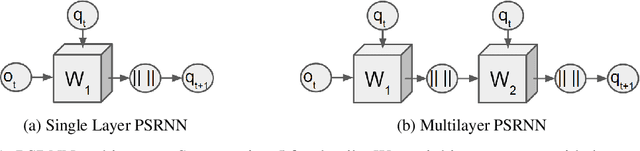
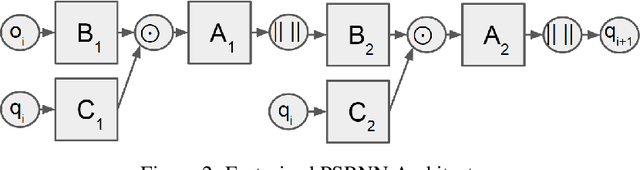
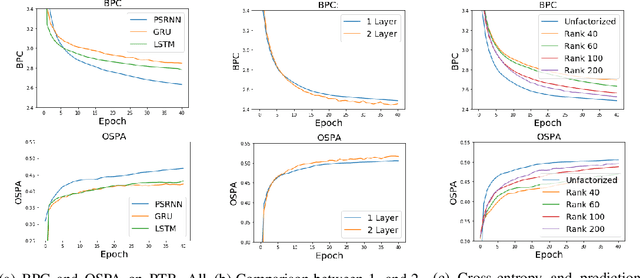
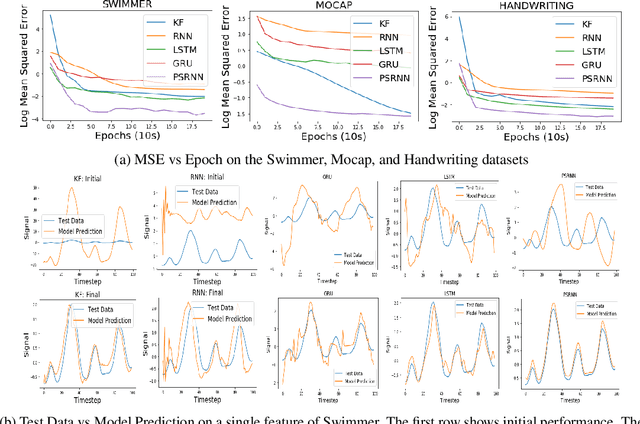
We present a new model, Predictive State Recurrent Neural Networks (PSRNNs), for filtering and prediction in dynamical systems. PSRNNs draw on insights from both Recurrent Neural Networks (RNNs) and Predictive State Representations (PSRs), and inherit advantages from both types of models. Like many successful RNN architectures, PSRNNs use (potentially deeply composed) bilinear transfer functions to combine information from multiple sources. We show that such bilinear functions arise naturally from state updates in Bayes filters like PSRs, in which observations can be viewed as gating belief states. We also show that PSRNNs can be learned effectively by combining Backpropogation Through Time (BPTT) with an initialization derived from a statistically consistent learning algorithm for PSRs called two-stage regression (2SR). Finally, we show that PSRNNs can be factorized using tensor decomposition, reducing model size and suggesting interesting connections to existing multiplicative architectures such as LSTMs. We applied PSRNNs to 4 datasets, and showed that we outperform several popular alternative approaches to modeling dynamical systems in all cases.

Practical Learning of Predictive State Representations

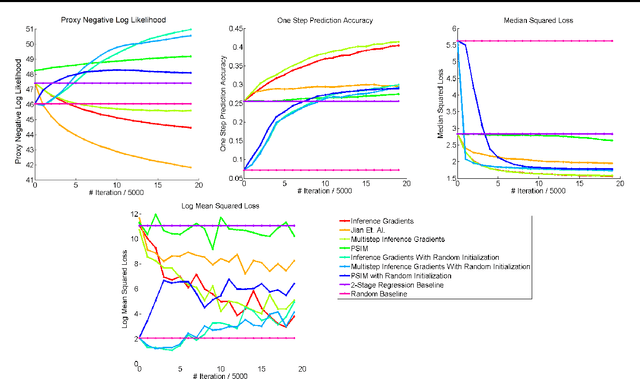
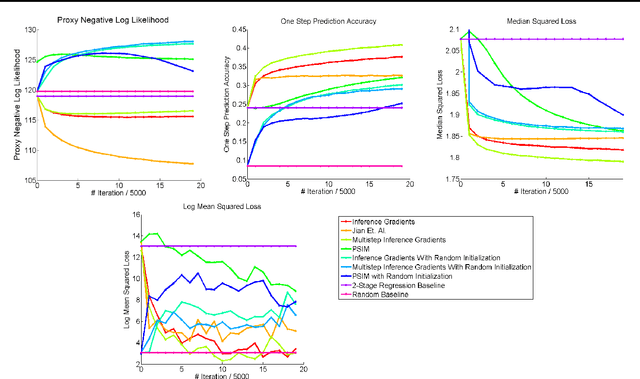
Over the past decade there has been considerable interest in spectral algorithms for learning Predictive State Representations (PSRs). Spectral algorithms have appealing theoretical guarantees; however, the resulting models do not always perform well on inference tasks in practice. One reason for this behavior is the mismatch between the intended task (accurate filtering or prediction) and the loss function being optimized by the algorithm (estimation error in model parameters). A natural idea is to improve performance by refining PSRs using an algorithm such as EM. Unfortunately it is not obvious how to apply apply an EM style algorithm in the context of PSRs as the Log Likelihood is not well defined for all PSRs. We show that it is possible to overcome this problem using ideas from Predictive State Inference Machines. We combine spectral algorithms for PSRs as a consistent and efficient initialization with PSIM-style updates to refine the resulting model parameters. By combining these two ideas we develop Inference Gradients, a simple, fast, and robust method for practical learning of PSRs. Inference Gradients performs gradient descent in the PSR parameter space to optimize an inference-based loss function like PSIM. Because Inference Gradients uses a spectral initialization we get the same consistency benefits as PSRs. We show that Inference Gradients outperforms both PSRs and PSIMs on real and synthetic data sets.

Stochastic Variance Reduction for Nonconvex Optimization

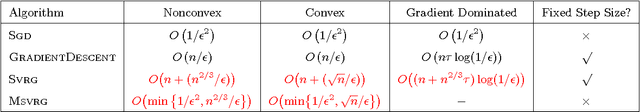
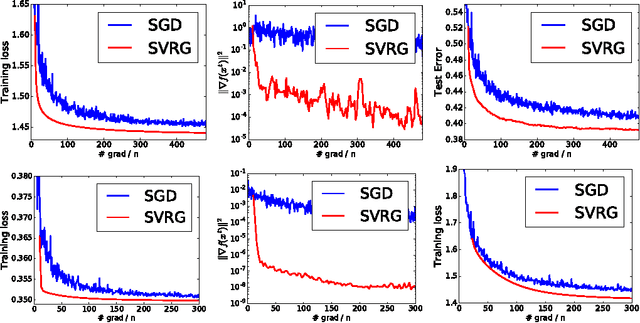
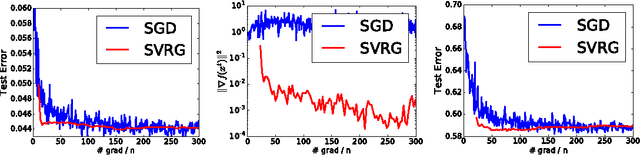
We study nonconvex finite-sum problems and analyze stochastic variance reduced gradient (SVRG) methods for them. SVRG and related methods have recently surged into prominence for convex optimization given their edge over stochastic gradient descent (SGD); but their theoretical analysis almost exclusively assumes convexity. In contrast, we prove non-asymptotic rates of convergence (to stationary points) of SVRG for nonconvex optimization, and show that it is provably faster than SGD and gradient descent. We also analyze a subclass of nonconvex problems on which SVRG attains linear convergence to the global optimum. We extend our analysis to mini-batch variants of SVRG, showing (theoretical) linear speedup due to mini-batching in parallel settings.

On Variance Reduction in Stochastic Gradient Descent and its Asynchronous Variants

We study optimization algorithms based on variance reduction for stochastic gradient descent (SGD). Remarkable recent progress has been made in this direction through development of algorithms like SAG, SVRG, SAGA. These algorithms have been shown to outperform SGD, both theoretically and empirically. However, asynchronous versions of these algorithms---a crucial requirement for modern large-scale applications---have not been studied. We bridge this gap by presenting a unifying framework for many variance reduction techniques. Subsequently, we propose an asynchronous algorithm grounded in our framework, and prove its fast convergence. An important consequence of our general approach is that it yields asynchronous versions of variance reduction algorithms such as SVRG and SAGA as a byproduct. Our method achieves near linear speedup in sparse settings common to machine learning. We demonstrate the empirical performance of our method through a concrete realization of asynchronous SVRG.

Supervised Learning for Dynamical System Learning

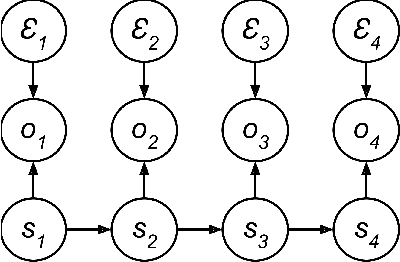
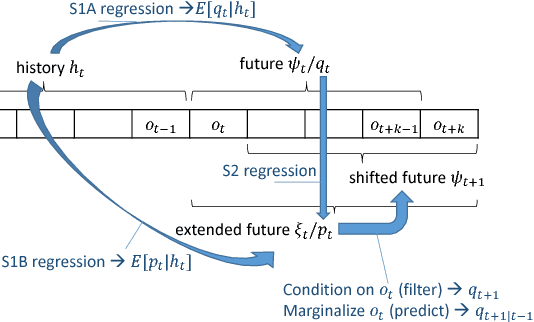
Recently there has been substantial interest in spectral methods for learning dynamical systems. These methods are popular since they often offer a good tradeoff between computational and statistical efficiency. Unfortunately, they can be difficult to use and extend in practice: e.g., they can make it difficult to incorporate prior information such as sparsity or structure. To address this problem, we present a new view of dynamical system learning: we show how to learn dynamical systems by solving a sequence of ordinary supervised learning problems, thereby allowing users to incorporate prior knowledge via standard techniques such as L1 regularization. Many existing spectral methods are special cases of this new framework, using linear regression as the supervised learner. We demonstrate the effectiveness of our framework by showing examples where nonlinear regression or lasso let us learn better state representations than plain linear regression does; the correctness of these instances follows directly from our general analysis.

Large-scale randomized-coordinate descent methods with non-separable linear constraints

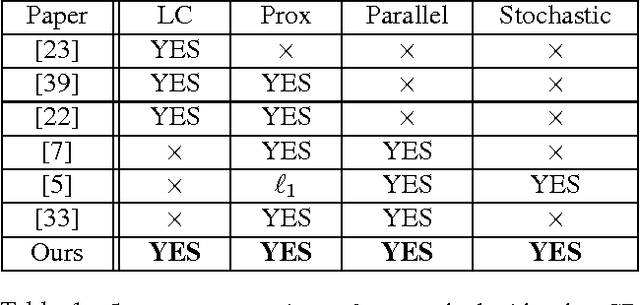
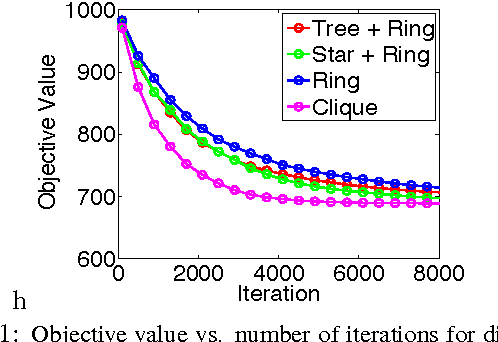
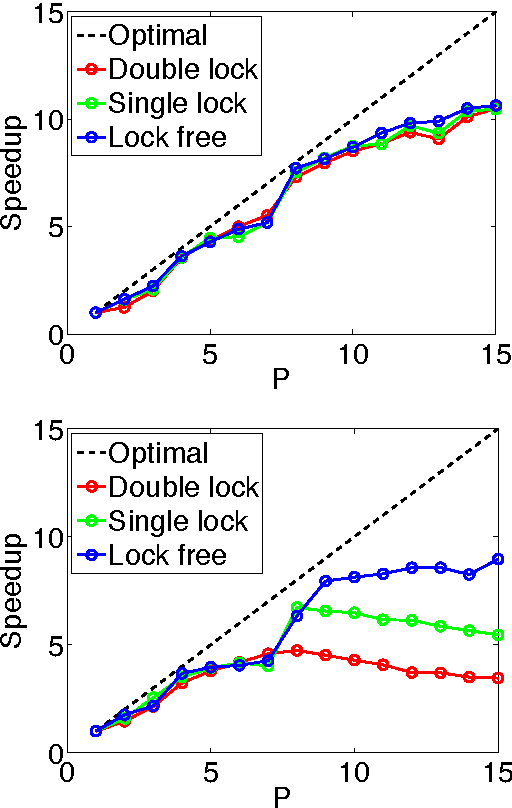
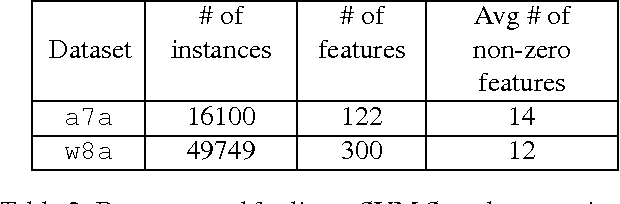
We develop randomized (block) coordinate descent (CD) methods for linearly constrained convex optimization. Unlike most CD methods, we do not assume the constraints to be separable, but let them be coupled linearly. To our knowledge, ours is the first CD method that allows linear coupling constraints, without making the global iteration complexity have an exponential dependence on the number of constraints. We present algorithms and analysis for four key problem scenarios: (i) smooth; (ii) smooth + nonsmooth separable; (iii) asynchronous parallel; and (iv) stochastic. We illustrate empirical behavior of our algorithms by simulation experiments.

A non-parametric mixture model for topic modeling over time

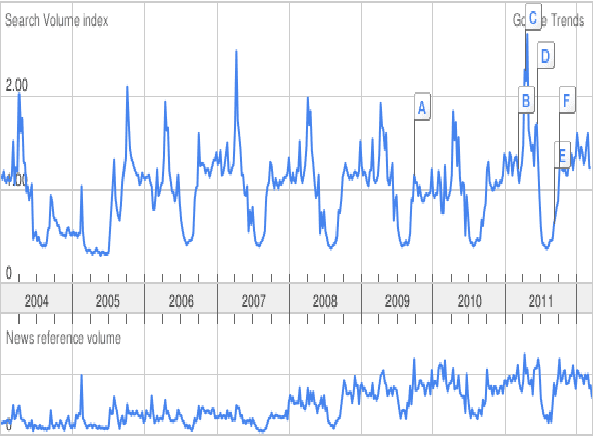
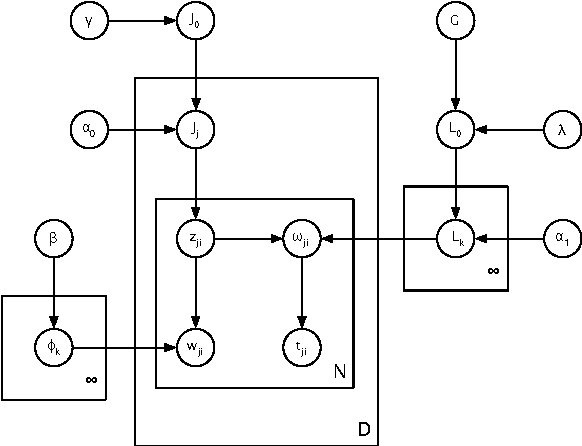
A single, stationary topic model such as latent Dirichlet allocation is inappropriate for modeling corpora that span long time periods, as the popularity of topics is likely to change over time. A number of models that incorporate time have been proposed, but in general they either exhibit limited forms of temporal variation, or require computationally expensive inference methods. In this paper we propose non-parametric Topics over Time (npTOT), a model for time-varying topics that allows an unbounded number of topics and exible distribution over the temporal variations in those topics' popularity. We develop a collapsed Gibbs sampler for the proposed model and compare against existing models on synthetic and real document sets.