Graph Adversarial Networks: Protecting Information against Adversarial Attacks

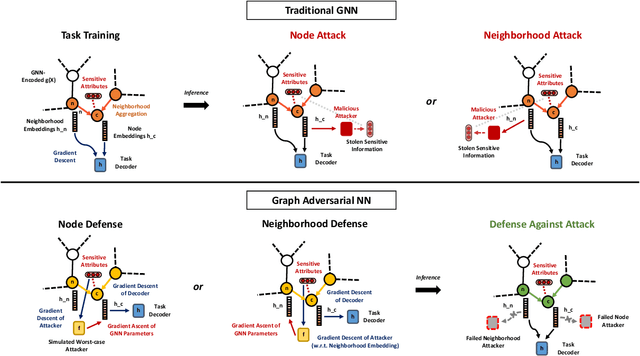
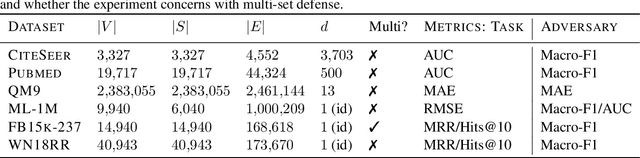
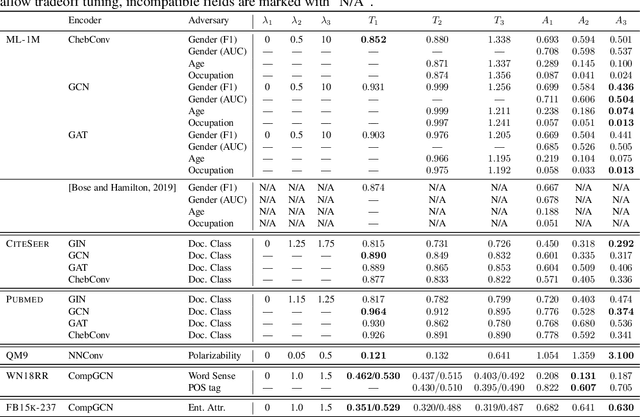
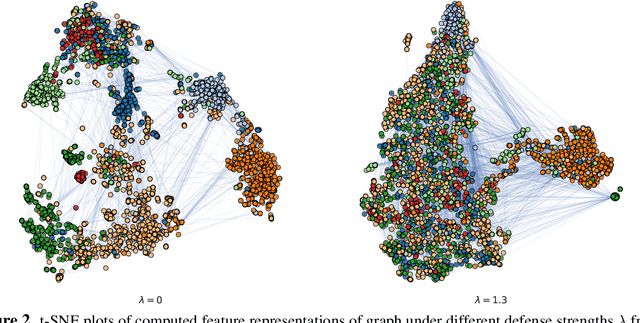
We study the problem of protecting information when learning with graph-structured data. While the advent of Graph Neural Networks (GNNs) has greatly improved node and graph representational learning in many applications, the neighborhood aggregation paradigm exposes additional vulnerabilities to attackers seeking to extract node-level information about sensitive attributes. To counter this, we propose a minimax game between the desired GNN encoder and the worst-case attacker. The resulting adversarial training creates a strong defense against inference attacks, while only suffering a small loss in task performance. We analyze the effectiveness of our framework against a worst-case adversary, and characterize the trade-off between predictive accuracy and adversarial defense. Experiments across multiple datasets from recommender systems, knowledge graphs and quantum chemistry demonstrate that the proposed approach provides a robust defense across various graph structures and tasks, while producing competitive GNN encoders. Our code is available at https://github.com/liaopeiyuan/GAL.

Towards modular and programmable architecture search

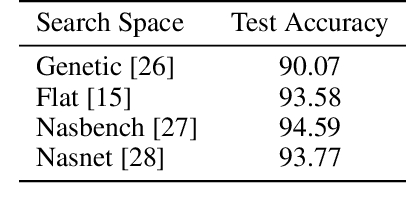
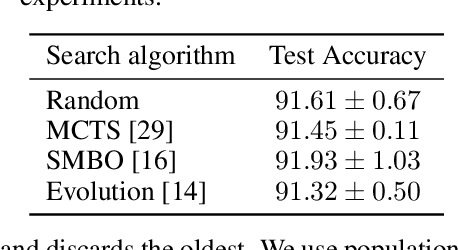
Neural architecture search methods are able to find high performance deep learning architectures with minimal effort from an expert. However, current systems focus on specific use-cases (e.g. convolutional image classifiers and recurrent language models), making them unsuitable for general use-cases that an expert might wish to write. Hyperparameter optimization systems are general-purpose but lack the constructs needed for easy application to architecture search. In this work, we propose a formal language for encoding search spaces over general computational graphs. The language constructs allow us to write modular, composable, and reusable search space encodings and to reason about search space design. We use our language to encode search spaces from the architecture search literature. The language allows us to decouple the implementations of the search space and the search algorithm, allowing us to expose search spaces to search algorithms through a consistent interface. Our experiments show the ease with which we can experiment with different combinations of search spaces and search algorithms without having to implement each combination from scratch. We release an implementation of our language with this paper.

Recurrent Predictive State Policy Networks

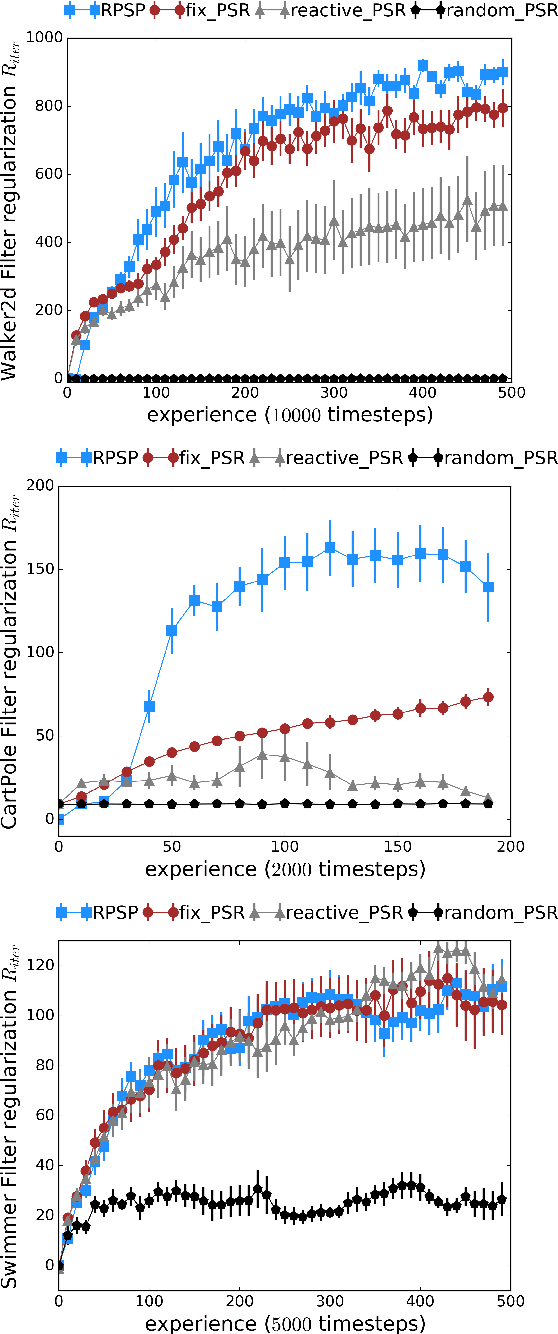
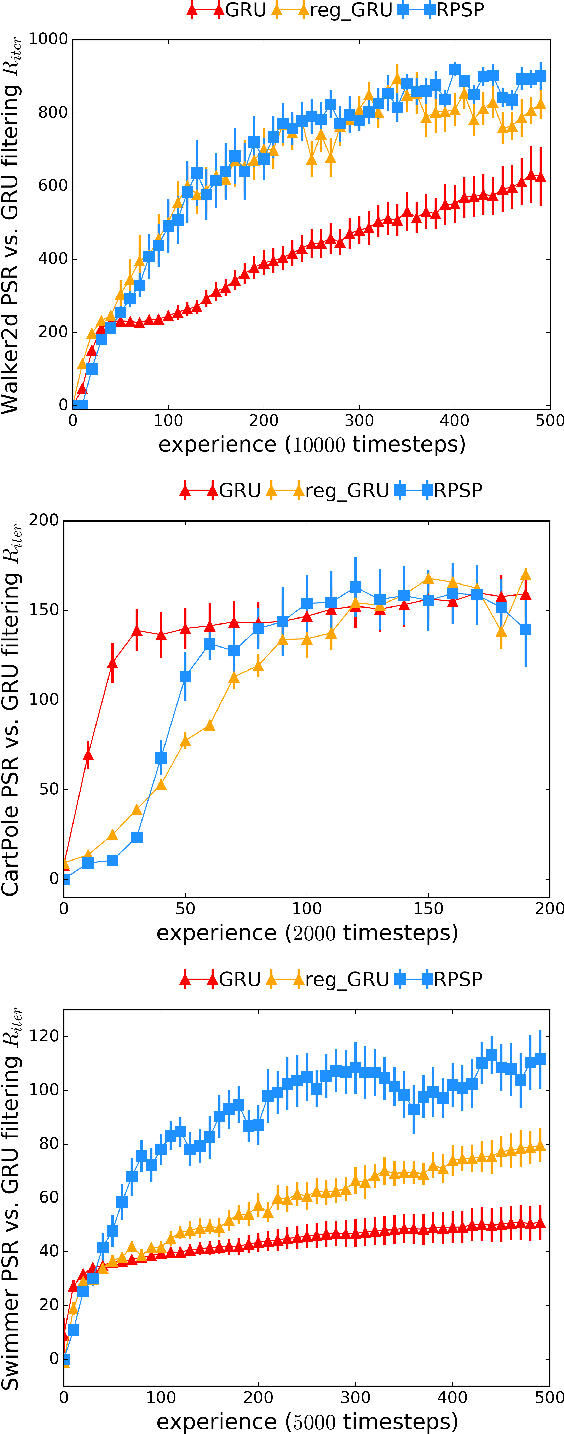
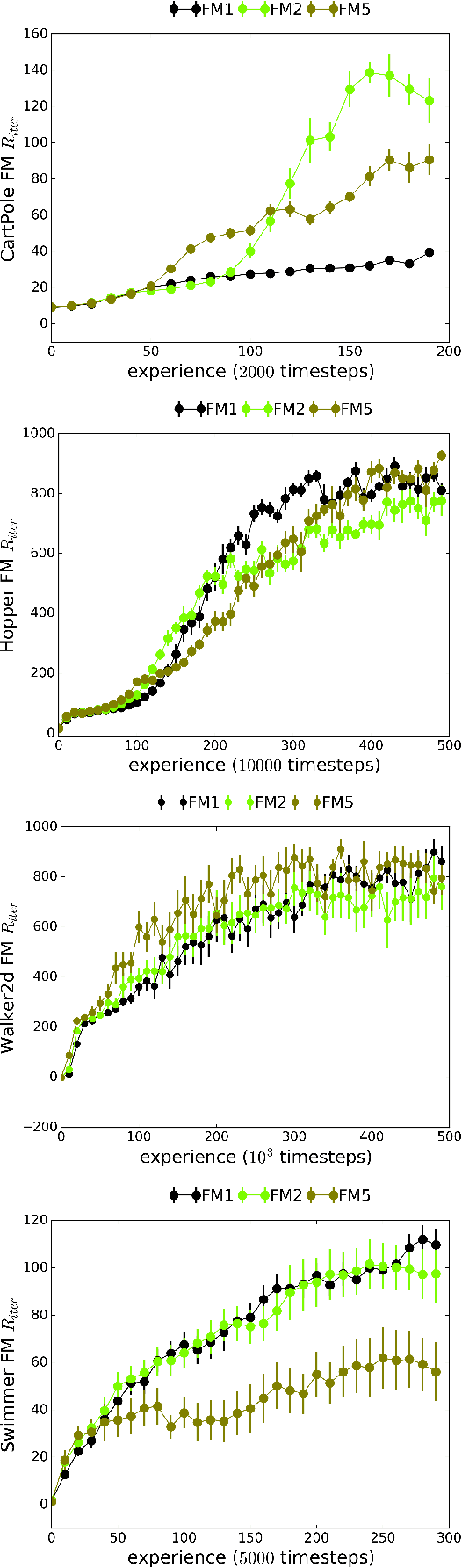
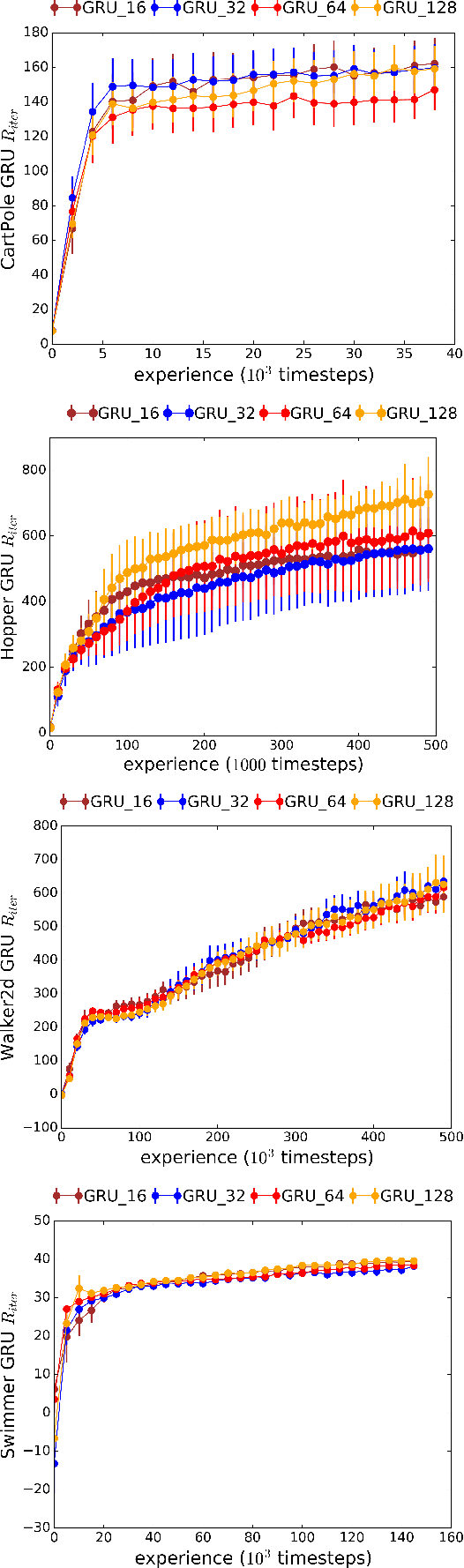
We introduce Recurrent Predictive State Policy (RPSP) networks, a recurrent architecture that brings insights from predictive state representations to reinforcement learning in partially observable environments. Predictive state policy networks consist of a recursive filter, which keeps track of a belief about the state of the environment, and a reactive policy that directly maps beliefs to actions, to maximize the cumulative reward. The recursive filter leverages predictive state representations (PSRs) (Rosencrantz and Gordon, 2004; Sun et al., 2016) by modeling predictive state-- a prediction of the distribution of future observations conditioned on history and future actions. This representation gives rise to a rich class of statistically consistent algorithms (Hefny et al., 2018) to initialize the recursive filter. Predictive state serves as an equivalent representation of a belief state. Therefore, the policy component of the RPSP-network can be purely reactive, simplifying training while still allowing optimal behaviour. Moreover, we use the PSR interpretation during training as well, by incorporating prediction error in the loss function. The entire network (recursive filter and reactive policy) is still differentiable and can be trained using gradient based methods. We optimize our policy using a combination of policy gradient based on rewards (Williams, 1992) and gradient descent based on prediction error. We show the efficacy of RPSP-networks under partial observability on a set of robotic control tasks from OpenAI Gym. We empirically show that RPSP-networks perform well compared with memory-preserving networks such as GRUs, as well as finite memory models, being the overall best performing method.

Learning General Latent-Variable Graphical Models with Predictive Belief Propagation and Hilbert Space Embeddings

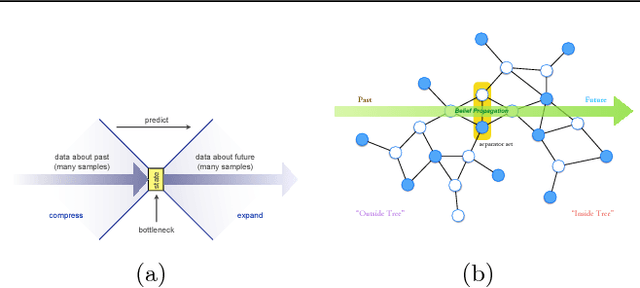
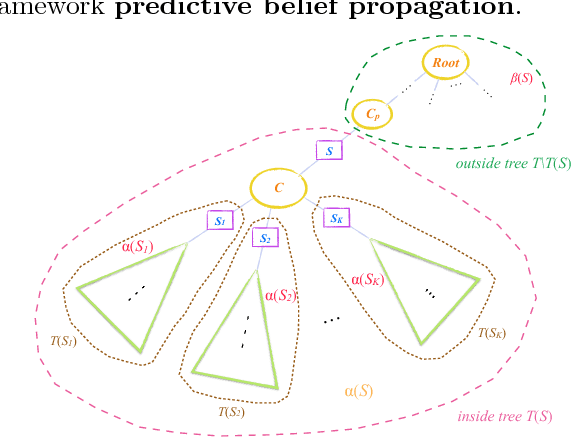
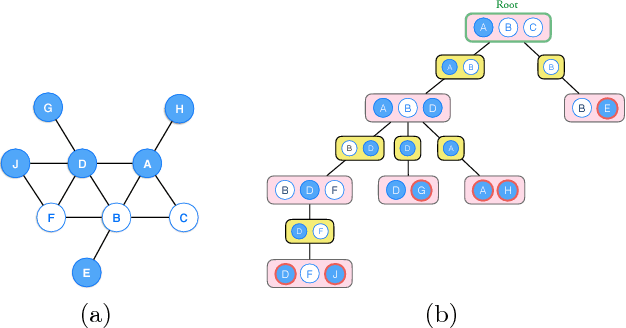
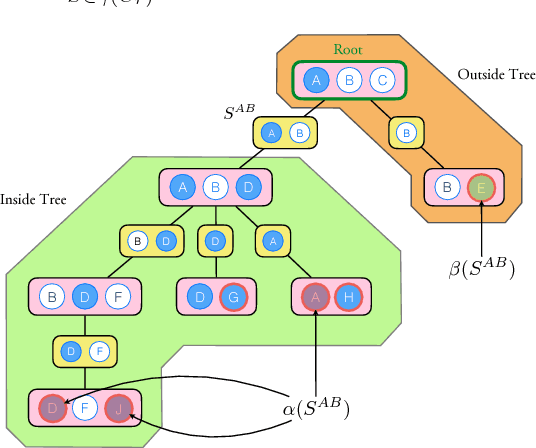
In this paper, we propose a new algorithm for learning general latent-variable probabilistic graphical models using the techniques of predictive state representation, instrumental variable regression, and reproducing-kernel Hilbert space embeddings of distributions. Under this new learning framework, we first convert latent-variable graphical models into corresponding latent-variable junction trees, and then reduce the hard parameter learning problem into a pipeline of supervised learning problems, whose results will then be used to perform predictive belief propagation over the latent junction tree during the actual inference procedure. We then give proofs of our algorithm's correctness, and demonstrate its good performance in experiments on one synthetic dataset and two real-world tasks from computational biology and computer vision - classifying DNA splice junctions and recognizing human actions in videos.

Predictive State Recurrent Neural Networks

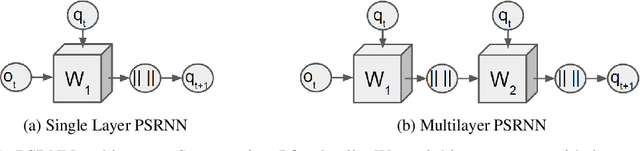
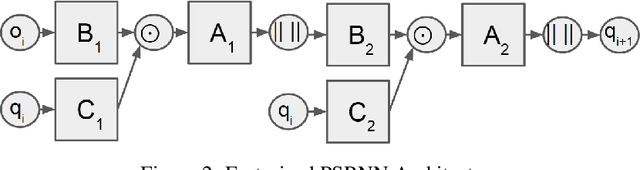
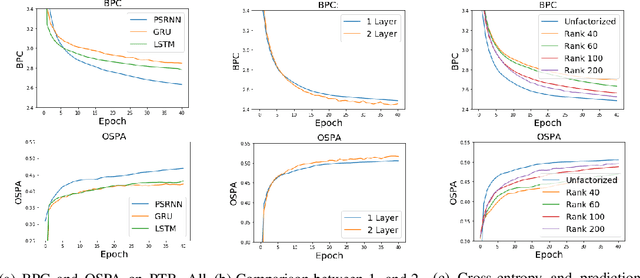
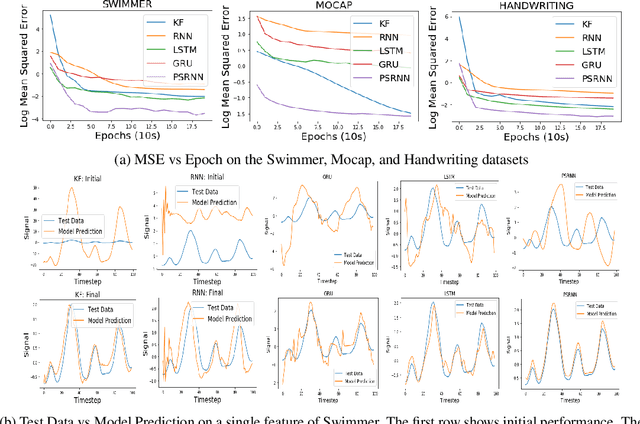
We present a new model, Predictive State Recurrent Neural Networks (PSRNNs), for filtering and prediction in dynamical systems. PSRNNs draw on insights from both Recurrent Neural Networks (RNNs) and Predictive State Representations (PSRs), and inherit advantages from both types of models. Like many successful RNN architectures, PSRNNs use (potentially deeply composed) bilinear transfer functions to combine information from multiple sources. We show that such bilinear functions arise naturally from state updates in Bayes filters like PSRs, in which observations can be viewed as gating belief states. We also show that PSRNNs can be learned effectively by combining Backpropogation Through Time (BPTT) with an initialization derived from a statistically consistent learning algorithm for PSRs called two-stage regression (2SR). Finally, we show that PSRNNs can be factorized using tensor decomposition, reducing model size and suggesting interesting connections to existing multiplicative architectures such as LSTMs. We applied PSRNNs to 4 datasets, and showed that we outperform several popular alternative approaches to modeling dynamical systems in all cases.

Practical Learning of Predictive State Representations

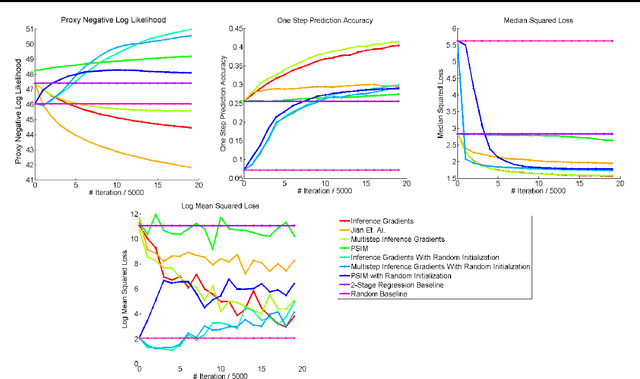
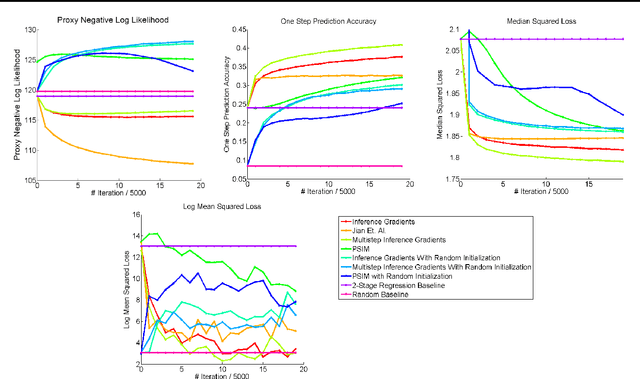
Over the past decade there has been considerable interest in spectral algorithms for learning Predictive State Representations (PSRs). Spectral algorithms have appealing theoretical guarantees; however, the resulting models do not always perform well on inference tasks in practice. One reason for this behavior is the mismatch between the intended task (accurate filtering or prediction) and the loss function being optimized by the algorithm (estimation error in model parameters). A natural idea is to improve performance by refining PSRs using an algorithm such as EM. Unfortunately it is not obvious how to apply apply an EM style algorithm in the context of PSRs as the Log Likelihood is not well defined for all PSRs. We show that it is possible to overcome this problem using ideas from Predictive State Inference Machines. We combine spectral algorithms for PSRs as a consistent and efficient initialization with PSIM-style updates to refine the resulting model parameters. By combining these two ideas we develop Inference Gradients, a simple, fast, and robust method for practical learning of PSRs. Inference Gradients performs gradient descent in the PSR parameter space to optimize an inference-based loss function like PSIM. Because Inference Gradients uses a spectral initialization we get the same consistency benefits as PSRs. We show that Inference Gradients outperforms both PSRs and PSIMs on real and synthetic data sets.

Functional Gradient Motion Planning in Reproducing Kernel Hilbert Spaces

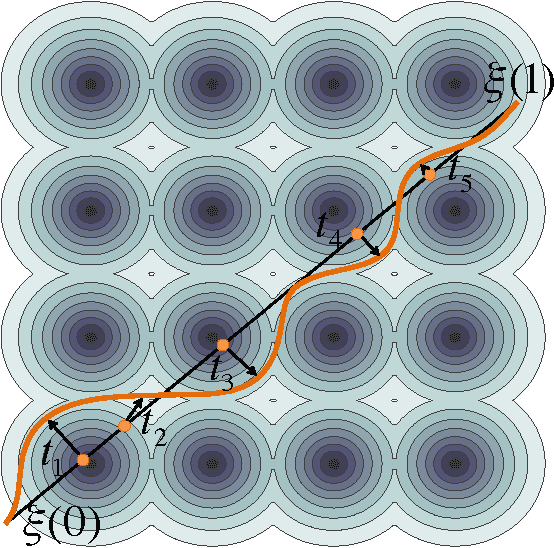
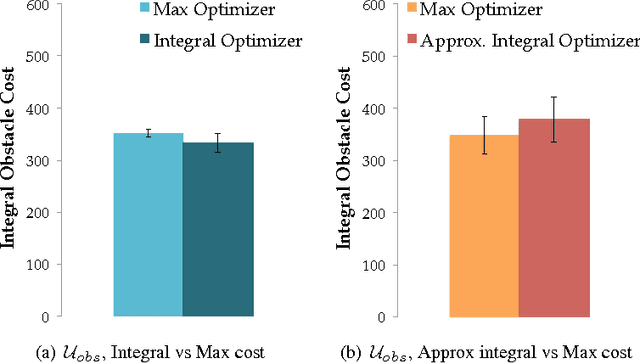
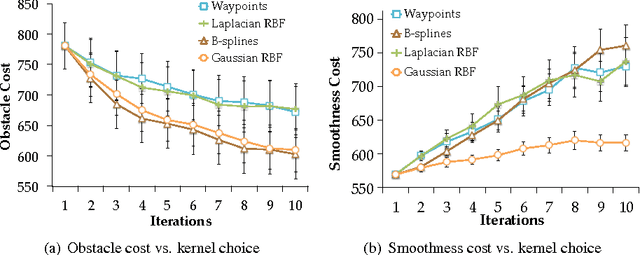
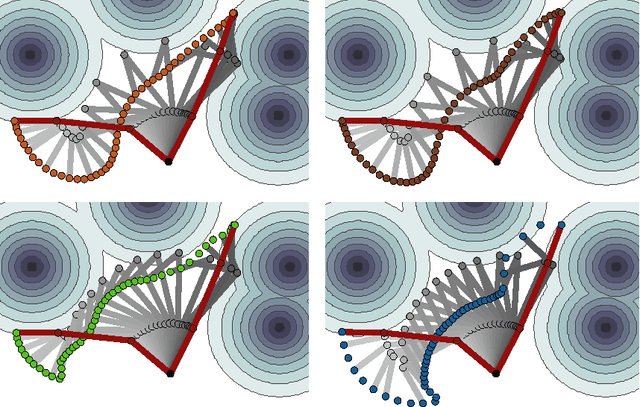
We introduce a functional gradient descent trajectory optimization algorithm for robot motion planning in Reproducing Kernel Hilbert Spaces (RKHSs). Functional gradient algorithms are a popular choice for motion planning in complex many-degree-of-freedom robots, since they (in theory) work by directly optimizing within a space of continuous trajectories to avoid obstacles while maintaining geometric properties such as smoothness. However, in practice, functional gradient algorithms typically commit to a fixed, finite parameterization of trajectories, often as a list of waypoints. Such a parameterization can lose much of the benefit of reasoning in a continuous trajectory space: e.g., it can require taking an inconveniently small step size and large number of iterations to maintain smoothness. Our work generalizes functional gradient trajectory optimization by formulating it as minimization of a cost functional in an RKHS. This generalization lets us represent trajectories as linear combinations of kernel functions, without any need for waypoints. As a result, we are able to take larger steps and achieve a locally optimal trajectory in just a few iterations. Depending on the selection of kernel, we can directly optimize in spaces of trajectories that are inherently smooth in velocity, jerk, curvature, etc., and that have a low-dimensional, adaptively chosen parameterization. Our experiments illustrate the effectiveness of the planner for different kernels, including Gaussian RBFs, Laplacian RBFs, and B-splines, as compared to the standard discretized waypoint representation.

Supervised Learning for Dynamical System Learning

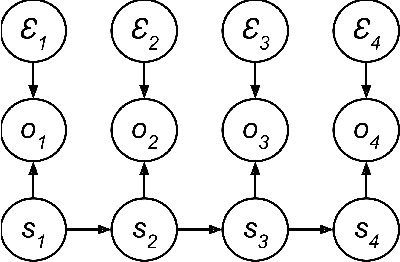
Recently there has been substantial interest in spectral methods for learning dynamical systems. These methods are popular since they often offer a good tradeoff between computational and statistical efficiency. Unfortunately, they can be difficult to use and extend in practice: e.g., they can make it difficult to incorporate prior information such as sparsity or structure. To address this problem, we present a new view of dynamical system learning: we show how to learn dynamical systems by solving a sequence of ordinary supervised learning problems, thereby allowing users to incorporate prior knowledge via standard techniques such as L1 regularization. Many existing spectral methods are special cases of this new framework, using linear regression as the supervised learner. We demonstrate the effectiveness of our framework by showing examples where nonlinear regression or lasso let us learn better state representations than plain linear regression does; the correctness of these instances follows directly from our general analysis.

Hilbert Space Embeddings of Predictive State Representations

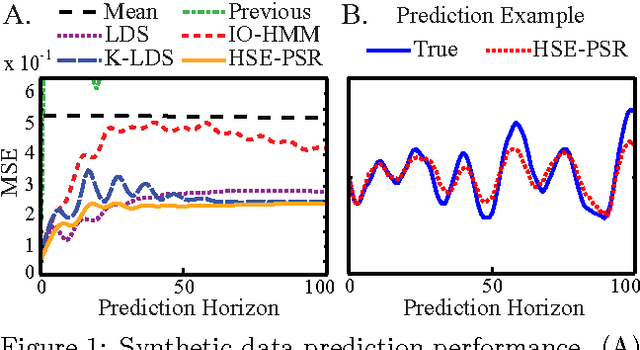
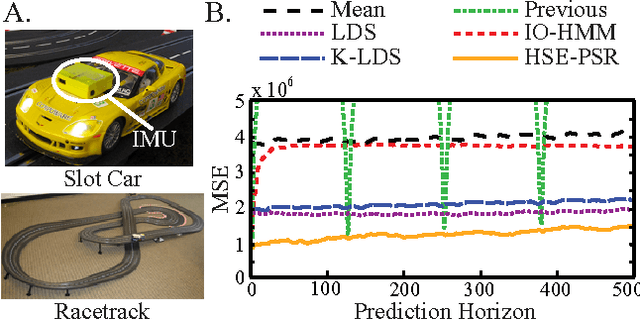
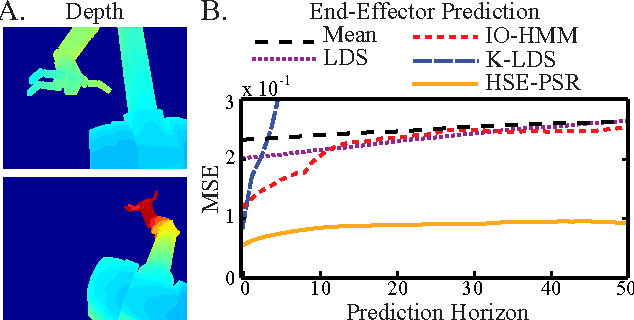
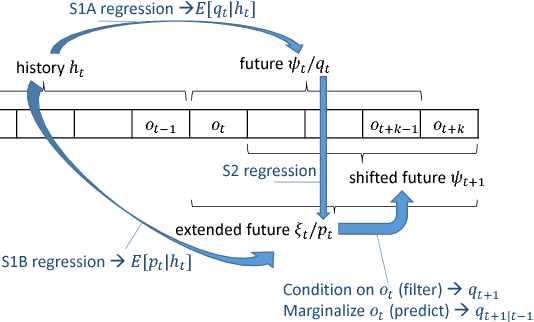
Predictive State Representations (PSRs) are an expressive class of models for controlled stochastic processes. PSRs represent state as a set of predictions of future observable events. Because PSRs are defined entirely in terms of observable data, statistically consistent estimates of PSR parameters can be learned efficiently by manipulating moments of observed training data. Most learning algorithms for PSRs have assumed that actions and observations are finite with low cardinality. In this paper, we generalize PSRs to infinite sets of observations and actions, using the recent concept of Hilbert space embeddings of distributions. The essence is to represent the state as a nonparametric conditional embedding operator in a Reproducing Kernel Hilbert Space (RKHS) and leverage recent work in kernel methods to estimate, predict, and update the representation. We show that these Hilbert space embeddings of PSRs are able to gracefully handle continuous actions and observations, and that our learned models outperform competing system identification algorithms on several prediction benchmarks.

Distributed Planning in Hierarchical Factored MDPs

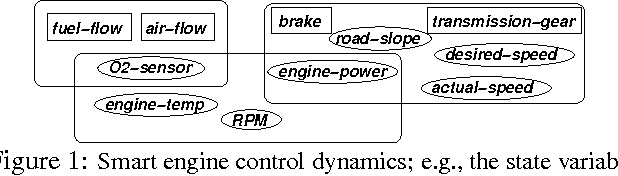
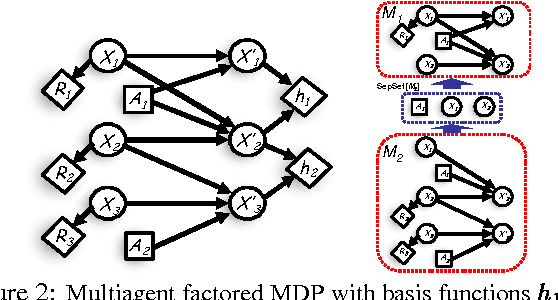
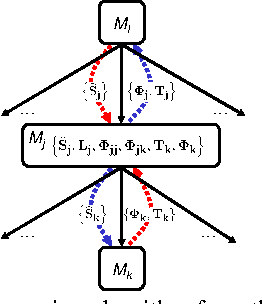
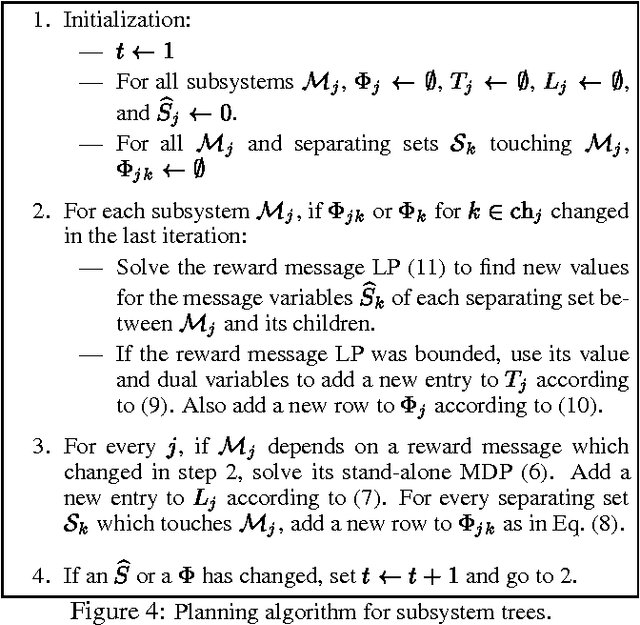
We present a principled and efficient planning algorithm for collaborative multiagent dynamical systems. All computation, during both the planning and the execution phases, is distributed among the agents; each agent only needs to model and plan for a small part of the system. Each of these local subsystems is small, but once they are combined they can represent an exponentially larger problem. The subsystems are connected through a subsystem hierarchy. Coordination and communication between the agents is not imposed, but derived directly from the structure of this hierarchy. A globally consistent plan is achieved by a message passing algorithm, where messages correspond to natural local reward functions and are computed by local linear programs; another message passing algorithm allows us to execute the resulting policy. When two portions of the hierarchy share the same structure, our algorithm can reuse plans and messages to speed up computation.