Risk-Sensitive Deep RL: Variance-Constrained Actor-Critic Provably Finds Globally Optimal Policy

While deep reinforcement learning has achieved tremendous successes in various applications, most existing works only focus on maximizing the expected value of total return and thus ignore its inherent stochasticity. Such stochasticity is also known as the aleatoric uncertainty and is closely related to the notion of risk. In this work, we make the first attempt to study risk-sensitive deep reinforcement learning under the average reward setting with the variance risk criteria. In particular, we focus on a variance-constrained policy optimization problem where the goal is to find a policy that maximizes the expected value of the long-run average reward, subject to a constraint that the long-run variance of the average reward is upper bounded by a threshold. Utilizing Lagrangian and Fenchel dualities, we transform the original problem into an unconstrained saddle-point policy optimization problem, and propose an actor-critic algorithm that iteratively and efficiently updates the policy, the Lagrange multiplier, and the Fenchel dual variable. When both the value and policy functions are represented by multi-layer overparameterized neural networks, we prove that our actor-critic algorithm generates a sequence of policies that finds a globally optimal policy at a sublinear rate.

Variational Transport: A Convergent Particle-BasedAlgorithm for Distributional Optimization

We consider the optimization problem of minimizing a functional defined over a family of probability distributions, where the objective functional is assumed to possess a variational form. Such a distributional optimization problem arises widely in machine learning and statistics, with Monte-Carlo sampling, variational inference, policy optimization, and generative adversarial network as examples. For this problem, we propose a novel particle-based algorithm, dubbed as variational transport, which approximately performs Wasserstein gradient descent over the manifold of probability distributions via iteratively pushing a set of particles. Specifically, we prove that moving along the geodesic in the direction of functional gradient with respect to the second-order Wasserstein distance is equivalent to applying a pushforward mapping to a probability distribution, which can be approximated accurately by pushing a set of particles. Specifically, in each iteration of variational transport, we first solve the variational problem associated with the objective functional using the particles, whose solution yields the Wasserstein gradient direction. Then we update the current distribution by pushing each particle along the direction specified by such a solution. By characterizing both the statistical error incurred in estimating the Wasserstein gradient and the progress of the optimization algorithm, we prove that when the objective function satisfies a functional version of the Polyak-\L{}ojasiewicz (PL) (Polyak, 1963) and smoothness conditions, variational transport converges linearly to the global minimum of the objective functional up to a certain statistical error, which decays to zero sublinearly as the number of particles goes to infinity.

Bridging Exploration and General Function Approximation in Reinforcement Learning: Provably Efficient Kernel and Neural Value Iterations

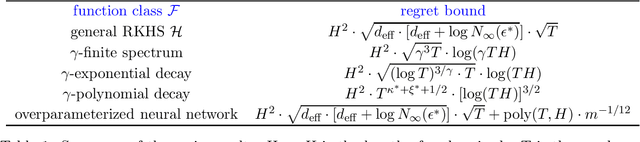
Reinforcement learning (RL) algorithms combined with modern function approximators such as kernel functions and deep neural networks have achieved significant empirical successes in large-scale application problems with a massive number of states. From a theoretical perspective, however, RL with functional approximation poses a fundamental challenge to developing algorithms with provable computational and statistical efficiency, due to the need to take into consideration both the exploration-exploitation tradeoff that is inherent in RL and the bias-variance tradeoff that is innate in statistical estimation. To address such a challenge, focusing on the episodic setting where the action-value functions are represented by a kernel function or over-parametrized neural network, we propose the first provable RL algorithm with both polynomial runtime and sample complexity, without additional assumptions on the data-generating model. In particular, for both the kernel and neural settings, we prove that an optimistic modification of the least-squares value iteration algorithm incurs an $\tilde{\mathcal{O}}(\delta_{\mathcal{F}} H^2 \sqrt{T})$ regret, where $\delta_{\mathcal{F}}$ characterizes the intrinsic complexity of the function class $\mathcal{F}$, $H$ is the length of each episode, and $T$ is the total number of episodes. Our regret bounds are independent of the number of states and therefore even allows it to diverge, which exhibits the benefit of function approximation.

Provable Fictitious Play for General Mean-Field Games

We propose a reinforcement learning algorithm for stationary mean-field games, where the goal is to learn a pair of mean-field state and stationary policy that constitutes the Nash equilibrium. When viewing the mean-field state and the policy as two players, we propose a fictitious play algorithm which alternatively updates the mean-field state and the policy via gradient-descent and proximal policy optimization, respectively. Our algorithm is in stark contrast with previous literature which solves each single-agent reinforcement learning problem induced by the iterates mean-field states to the optimum. Furthermore, we prove that our fictitious play algorithm converges to the Nash equilibrium at a sublinear rate. To the best of our knowledge, this seems the first provably convergent single-loop reinforcement learning algorithm for mean-field games based on iterative updates of both mean-field state and policy.

Single-Timescale Stochastic Nonconvex-Concave Optimization for Smooth Nonlinear TD Learning

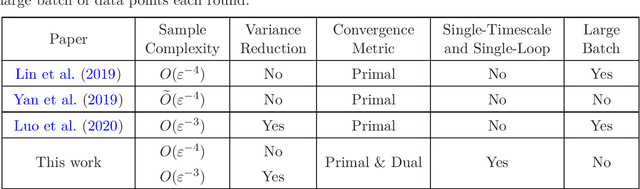
Temporal-Difference (TD) learning with nonlinear smooth function approximation for policy evaluation has achieved great success in modern reinforcement learning. It is shown that such a problem can be reformulated as a stochastic nonconvex-strongly-concave optimization problem, which is challenging as naive stochastic gradient descent-ascent algorithm suffers from slow convergence. Existing approaches for this problem are based on two-timescale or double-loop stochastic gradient algorithms, which may also require sampling large-batch data. However, in practice, a single-timescale single-loop stochastic algorithm is preferred due to its simplicity and also because its step-size is easier to tune. In this paper, we propose two single-timescale single-loop algorithms which require only one data point each step. Our first algorithm implements momentum updates on both primal and dual variables achieving an $O(\varepsilon^{-4})$ sample complexity, which shows the important role of momentum in obtaining a single-timescale algorithm. Our second algorithm improves upon the first one by applying variance reduction on top of momentum, which matches the best known $O(\varepsilon^{-3})$ sample complexity in existing works. Furthermore, our variance-reduction algorithm does not require a large-batch checkpoint. Moreover, our theoretical results for both algorithms are expressed in a tighter form of simultaneous primal and dual side convergence.

Global Convergence of Policy Gradient for Linear-Quadratic Mean-Field Control/Game in Continuous Time

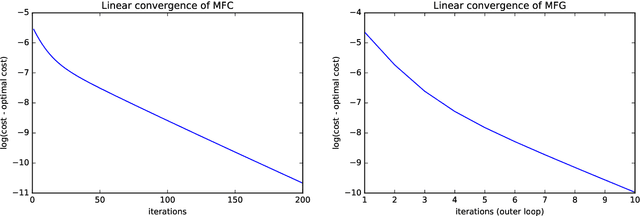
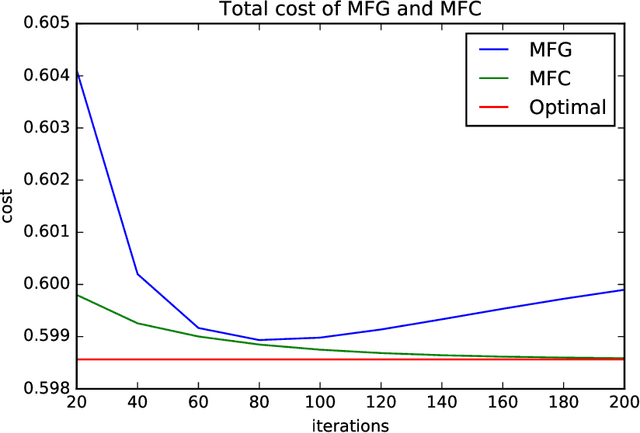
Reinforcement learning is a powerful tool to learn the optimal policy of possibly multiple agents by interacting with the environment. As the number of agents grow to be very large, the system can be approximated by a mean-field problem. Therefore, it has motivated new research directions for mean-field control (MFC) and mean-field game (MFG). In this paper, we study the policy gradient method for the linear-quadratic mean-field control and game, where we assume each agent has identical linear state transitions and quadratic cost functions. While most of the recent works on policy gradient for MFC and MFG are based on discrete-time models, we focus on the continuous-time models where some analyzing techniques can be interesting to the readers. For both MFC and MFG, we provide policy gradient update and show that it converges to the optimal solution at a linear rate, which is verified by a synthetic simulation. For MFG, we also provide sufficient conditions for the existence and uniqueness of the Nash equilibrium.

Single-Timescale Actor-Critic Provably Finds Globally Optimal Policy

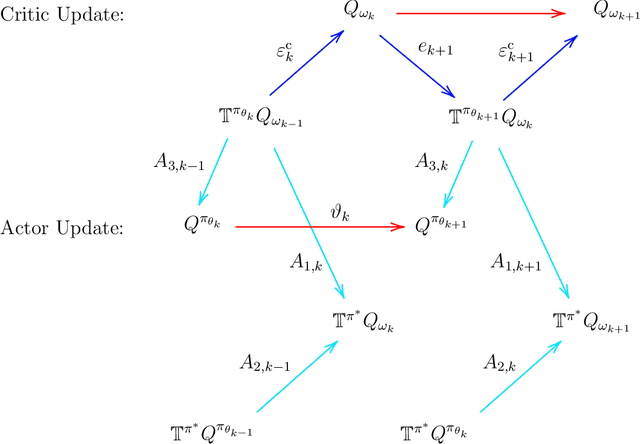
We study the global convergence and global optimality of actor-critic, one of the most popular families of reinforcement learning algorithms. While most existing works on actor-critic employ bi-level or two-timescale updates, we focus on the more practical single-timescale setting, where the actor and critic are updated simultaneously. Specifically, in each iteration, the critic update is obtained by applying the Bellman evaluation operator only once while the actor is updated in the policy gradient direction computed using the critic. Moreover, we consider two function approximation settings where both the actor and critic are represented by linear or deep neural networks. For both cases, we prove that the actor sequence converges to a globally optimal policy at a sublinear $O(K^{-1/2})$ rate, where $K$ is the number of iterations. To the best of our knowledge, we establish the rate of convergence and global optimality of single-timescale actor-critic with linear function approximation for the first time. Moreover, under the broader scope of policy optimization with nonlinear function approximation, we prove that actor-critic with deep neural network finds the globally optimal policy at a sublinear rate for the first time.

Understanding Implicit Regularization in Over-Parameterized Nonlinear Statistical Model

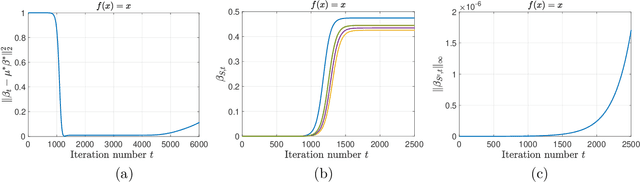
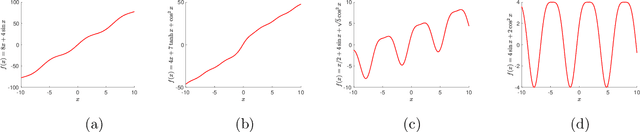
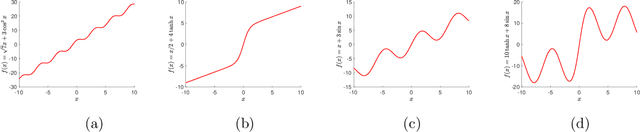
We study the implicit regularization phenomenon induced by simple optimization algorithms in over-parameterized nonlinear statistical models. Specifically, we study both vector and matrix single index models where the link function is nonlinear and unknown, the signal parameter is either a sparse vector or a low-rank symmetric matrix, and the response variable can be heavy-tailed. To gain a better understanding the role of implicit regularization in the nonlinear models without excess technicality, we assume that the distribution of the covariates is known as a priori. For both the vector and matrix settings, we construct an over-parameterized least-squares loss function by employing the score function transform and a robust truncation step designed specifically for heavy-tailed data. We propose to estimate the true parameter by applying regularization-free gradient descent to the loss function. When the initialization is close to the origin and the stepsize is sufficiently small, we prove that the obtained solution achieves minimax optimal statistical rates of convergence in both the vector and matrix cases. In particular, for the vector single index model with Gaussian covariates, our proposed estimator is shown to enjoy the oracle statistical rate. Our results capture the implicit regularization phenomenon in over-parameterized nonlinear and noisy statistical models with possibly heavy-tailed data.

A Two-Timescale Framework for Bilevel Optimization: Complexity Analysis and Application to Actor-Critic

This paper analyzes a two-timescale stochastic algorithm for a class of bilevel optimization problems with applications such as policy optimization in reinforcement learning, hyperparameter optimization, among others. We consider a case when the inner problem is unconstrained and strongly convex, and the outer problem is either strongly convex, convex or weakly convex. We propose a nonlinear two-timescale stochastic approximation (TTSA) algorithm for tackling the bilevel optimization. In the algorithm, a stochastic (semi)gradient update with a larger step size (faster timescale) is used for the inner problem, while a stochastic mirror descent update with a smaller step size (slower timescale) is used for the outer problem. When the outer problem is strongly convex (resp. weakly convex), the TTSA algorithm finds an $\mathcal{O}(K^{-1/2})$-optimal (resp. $\mathcal{O}(K^{-2/5})$-stationary) solution, where $K$ is the iteration number. To our best knowledge, these are the first convergence rate results for using nonlinear TTSA algorithms on the concerned class of bilevel optimization problems. Lastly, specific to the application of policy optimization, we show that a two-timescale actor-critic proximal policy optimization algorithm can be viewed as a special case of our framework. The actor-critic algorithm converges at $\mathcal{O}(K^{-1/4})$ in terms of the gap in objective value to a globally optimal policy.

Provably Efficient Neural Estimation of Structural Equation Model: An Adversarial Approach

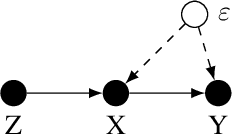
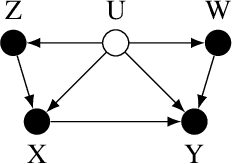
Structural equation models (SEMs) are widely used in sciences, ranging from economics to psychology, to uncover causal relationships underlying a complex system under consideration and estimate structural parameters of interest. We study estimation in a class of generalized SEMs where the object of interest is defined as the solution to a linear operator equation. We formulate the linear operator equation as a min-max game, where both players are parameterized by neural networks (NNs), and learn the parameters of these neural networks using the stochastic gradient descent. We consider both 2-layer and multi-layer NNs with ReLU activation functions and prove global convergence in an overparametrized regime, where the number of neurons is diverging. The results are established using techniques from online learning and local linearization of NNs, and improve in several aspects the current state-of-the-art. For the first time we provide a tractable estimation procedure for SEMs based on NNs with provable convergence and without the need for sample splitting.