What Happens Next? Next Scene Prediction with a Unified Video Model

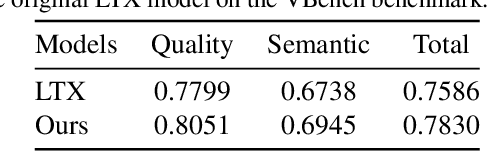
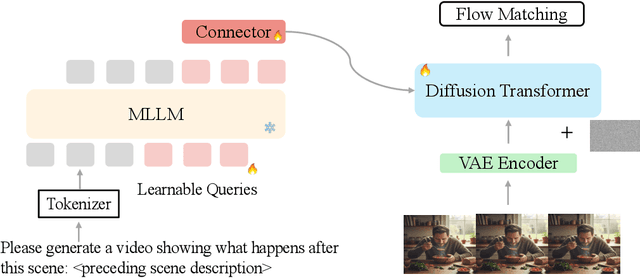
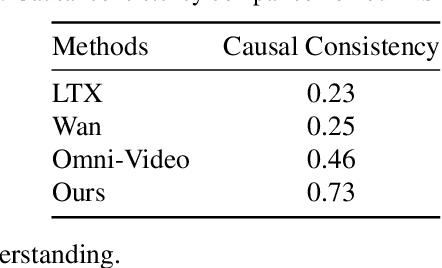
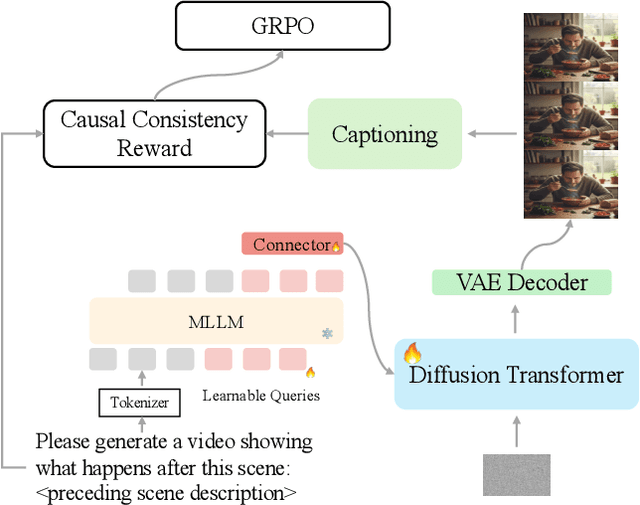
Recent unified models for joint understanding and generation have significantly advanced visual generation capabilities. However, their focus on conventional tasks like text-to-video generation has left the temporal reasoning potential of unified models largely underexplored. To address this gap, we introduce Next Scene Prediction (NSP), a new task that pushes unified video models toward temporal and causal reasoning. Unlike text-to-video generation, NSP requires predicting plausible futures from preceding context, demanding deeper understanding and reasoning. To tackle this task, we propose a unified framework combining Qwen-VL for comprehension and LTX for synthesis, bridged by a latent query embedding and a connector module. This model is trained in three stages on our newly curated, large-scale NSP dataset: text-to-video pre-training, supervised fine-tuning, and reinforcement learning (via GRPO) with our proposed causal consistency reward. Experiments demonstrate our model achieves state-of-the-art performance on our benchmark, advancing the capability of generalist multimodal systems to anticipate what happens next.

VIDEOP2R: Video Understanding from Perception to Reasoning

Reinforcement fine-tuning (RFT), a two-stage framework consisting of supervised fine-tuning (SFT) and reinforcement learning (RL) has shown promising results on improving reasoning ability of large language models (LLMs). Yet extending RFT to large video language models (LVLMs) remains challenging. We propose VideoP2R, a novel process-aware video RFT framework that enhances video reasoning by modeling perception and reasoning as distinct processes. In the SFT stage, we develop a three-step pipeline to generate VideoP2R-CoT-162K, a high-quality, process-aware chain-of-thought (CoT) dataset for perception and reasoning. In the RL stage, we introduce a novel process-aware group relative policy optimization (PA-GRPO) algorithm that supplies separate rewards for perception and reasoning. Extensive experiments show that VideoP2R achieves state-of-the-art (SotA) performance on six out of seven video reasoning and understanding benchmarks. Ablation studies further confirm the effectiveness of our process-aware modeling and PA-GRPO and demonstrate that model's perception output is information-sufficient for downstream reasoning.

A Random Matrix Perspective of Echo State Networks: From Precise Bias--Variance Characterization to Optimal Regularization

We present a rigorous asymptotic analysis of Echo State Networks (ESNs) in a teacher student setting with a linear teacher with oracle weights. Leveraging random matrix theory, we derive closed form expressions for the asymptotic bias, variance, and mean-squared error (MSE) as functions of the input statistics, the oracle vector, and the ridge regularization parameter. The analysis reveals two key departures from classical ridge regression: (i) ESNs do not exhibit double descent, and (ii) ESNs attain lower MSE when both the number of training samples and the teacher memory length are limited. We further provide an explicit formula for the optimal regularization in the identity input covariance case, and propose an efficient numerical scheme to compute the optimum in the general case. Together, these results offer interpretable theory and practical guidelines for tuning ESNs, helping reconcile recent empirical observations with provable performance guarantees

Random Matrix Theory for Deep Learning: Beyond Eigenvalues of Linear Models

Modern Machine Learning (ML) and Deep Neural Networks (DNNs) often operate on high-dimensional data and rely on overparameterized models, where classical low-dimensional intuitions break down. In particular, the proportional regime where the data dimension, sample size, and number of model parameters are all large and comparable, gives rise to novel and sometimes counterintuitive behaviors. This paper extends traditional Random Matrix Theory (RMT) beyond eigenvalue-based analysis of linear models to address the challenges posed by nonlinear ML models such as DNNs in this regime. We introduce the concept of High-dimensional Equivalent, which unifies and generalizes both Deterministic Equivalent and Linear Equivalent, to systematically address three technical challenges: high dimensionality, nonlinearity, and the need to analyze generic eigenspectral functionals. Leveraging this framework, we provide precise characterizations of the training and generalization performance of linear models, nonlinear shallow networks, and deep networks. Our results capture rich phenomena, including scaling laws, double descent, and nonlinear learning dynamics, offering a unified perspective on the theoretical understanding of deep learning in high dimensions.

Fundamental Bias in Inverting Random Sampling Matrices with Application to Sub-sampled Newton

A substantial body of work in machine learning (ML) and randomized numerical linear algebra (RandNLA) has exploited various sorts of random sketching methodologies, including random sampling and random projection, with much of the analysis using Johnson--Lindenstrauss and subspace embedding techniques. Recent studies have identified the issue of inversion bias -- the phenomenon that inverses of random sketches are not unbiased, despite the unbiasedness of the sketches themselves. This bias presents challenges for the use of random sketches in various ML pipelines, such as fast stochastic optimization, scalable statistical estimators, and distributed optimization. In the context of random projection, the inversion bias can be easily corrected for dense Gaussian projections (which are, however, too expensive for many applications). Recent work has shown how the inversion bias can be corrected for sparse sub-gaussian projections. In this paper, we show how the inversion bias can be corrected for random sampling methods, both uniform and non-uniform leverage-based, as well as for structured random projections, including those based on the Hadamard transform. Using these results, we establish problem-independent local convergence rates for sub-sampled Newton methods.

A Large-dimensional Analysis of ESPRIT DoA Estimation: Inconsistency and a Correction via RMT

In this paper, we perform asymptotic analyses of the widely used ESPRIT direction-of-arrival (DoA) estimator for large arrays, where the array size $N$ and the number of snapshots $T$ grow to infinity at the same pace. In this large-dimensional regime, the sample covariance matrix (SCM) is known to be a poor eigenspectral estimator of the population covariance. We show that the classical ESPRIT algorithm, that relies on the SCM, and as a consequence of the large-dimensional inconsistency of the SCM, produces inconsistent DoA estimates as $N,T \to \infty$ with $N/T \to c \in (0,\infty)$, for both widely- and closely-spaced DoAs. Leveraging tools from random matrix theory (RMT), we propose an improved G-ESPRIT method and prove its consistency in the same large-dimensional setting. From a technical perspective, we derive a novel bound on the eigenvalue differences between two potentially non-Hermitian random matrices, which may be of independent interest. Numerical simulations are provided to corroborate our theoretical findings.

The Breakdown of Gaussian Universality in Classification of High-dimensional Mixtures

The assumption of Gaussian or Gaussian mixture data has been extensively exploited in a long series of precise performance analyses of machine learning (ML) methods, on large datasets having comparably numerous samples and features. To relax this restrictive assumption, subsequent efforts have been devoted to establish "Gaussian equivalent principles" by studying scenarios of Gaussian universality where the asymptotic performance of ML methods on non-Gaussian data remains unchanged when replaced with Gaussian data having the same mean and covariance. Beyond the realm of Gaussian universality, there are few exact results on how the data distribution affects the learning performance. In this article, we provide a precise high-dimensional characterization of empirical risk minimization, for classification under a general mixture data setting of linear factor models that extends Gaussian mixtures. The Gaussian universality is shown to break down under this setting, in the sense that the asymptotic learning performance depends on the data distribution beyond the class means and covariances. To clarify the limitations of Gaussian universality in classification of mixture data and to understand the impact of its breakdown, we specify conditions for Gaussian universality and discuss their implications for the choice of loss function.

"Lossless" Compression of Deep Neural Networks: A High-dimensional Neural Tangent Kernel Approach

Modern deep neural networks (DNNs) are extremely powerful; however, this comes at the price of increased depth and having more parameters per layer, making their training and inference more computationally challenging. In an attempt to address this key limitation, efforts have been devoted to the compression (e.g., sparsification and/or quantization) of these large-scale machine learning models, so that they can be deployed on low-power IoT devices. In this paper, building upon recent advances in neural tangent kernel (NTK) and random matrix theory (RMT), we provide a novel compression approach to wide and fully-connected \emph{deep} neural nets. Specifically, we demonstrate that in the high-dimensional regime where the number of data points $n$ and their dimension $p$ are both large, and under a Gaussian mixture model for the data, there exists \emph{asymptotic spectral equivalence} between the NTK matrices for a large family of DNN models. This theoretical result enables "lossless" compression of a given DNN to be performed, in the sense that the compressed network yields asymptotically the same NTK as the original (dense and unquantized) network, with its weights and activations taking values \emph{only} in $\{ 0, \pm 1 \}$ up to a scaling. Experiments on both synthetic and real-world data are conducted to support the advantages of the proposed compression scheme, with code available at \url{https://github.com/Model-Compression/Lossless_Compression}.

Deep Equilibrium Models are Almost Equivalent to Not-so-deep Explicit Models for High-dimensional Gaussian Mixtures

Deep equilibrium models (DEQs), as a typical implicit neural network, have demonstrated remarkable success on various tasks. There is, however, a lack of theoretical understanding of the connections and differences between implicit DEQs and explicit neural network models. In this paper, leveraging recent advances in random matrix theory (RMT), we perform an in-depth analysis on the eigenspectra of the conjugate kernel (CK) and neural tangent kernel (NTK) matrices for implicit DEQs, when the input data are drawn from a high-dimensional Gaussian mixture. We prove, in this setting, that the spectral behavior of these Implicit-CKs and NTKs depend on the DEQ activation function and initial weight variances, but only via a system of four nonlinear equations. As a direct consequence of this theoretical result, we demonstrate that a shallow explicit network can be carefully designed to produce the same CK or NTK as a given DEQ. Despite derived here for Gaussian mixture data, empirical results show the proposed theory and design principle also apply to popular real-world datasets.

Robust and Communication-Efficient Federated Domain Adaptation via Random Features

Modern machine learning (ML) models have grown to a scale where training them on a single machine becomes impractical. As a result, there is a growing trend to leverage federated learning (FL) techniques to train large ML models in a distributed and collaborative manner. These models, however, when deployed on new devices, might struggle to generalize well due to domain shifts. In this context, federated domain adaptation (FDA) emerges as a powerful approach to address this challenge. Most existing FDA approaches typically focus on aligning the distributions between source and target domains by minimizing their (e.g., MMD) distance. Such strategies, however, inevitably introduce high communication overheads and can be highly sensitive to network reliability. In this paper, we introduce RF-TCA, an enhancement to the standard Transfer Component Analysis approach that significantly accelerates computation without compromising theoretical and empirical performance. Leveraging the computational advantage of RF-TCA, we further extend it to FDA setting with FedRF-TCA. The proposed FedRF-TCA protocol boasts communication complexity that is \emph{independent} of the sample size, while maintaining performance that is either comparable to or even surpasses state-of-the-art FDA methods. We present extensive experiments to showcase the superior performance and robustness (to network condition) of FedRF-TCA.