On Path to Multimodal Historical Reasoning: HistBench and HistAgent

Recent advances in large language models (LLMs) have led to remarkable progress across domains, yet their capabilities in the humanities, particularly history, remain underexplored. Historical reasoning poses unique challenges for AI, involving multimodal source interpretation, temporal inference, and cross-linguistic analysis. While general-purpose agents perform well on many existing benchmarks, they lack the domain-specific expertise required to engage with historical materials and questions. To address this gap, we introduce HistBench, a new benchmark of 414 high-quality questions designed to evaluate AI's capacity for historical reasoning and authored by more than 40 expert contributors. The tasks span a wide range of historical problems-from factual retrieval based on primary sources to interpretive analysis of manuscripts and images, to interdisciplinary challenges involving archaeology, linguistics, or cultural history. Furthermore, the benchmark dataset spans 29 ancient and modern languages and covers a wide range of historical periods and world regions. Finding the poor performance of LLMs and other agents on HistBench, we further present HistAgent, a history-specific agent equipped with carefully designed tools for OCR, translation, archival search, and image understanding in History. On HistBench, HistAgent based on GPT-4o achieves an accuracy of 27.54% pass@1 and 36.47% pass@2, significantly outperforming LLMs with online search and generalist agents, including GPT-4o (18.60%), DeepSeek-R1(14.49%) and Open Deep Research-smolagents(20.29% pass@1 and 25.12% pass@2). These results highlight the limitations of existing LLMs and generalist agents and demonstrate the advantages of HistAgent for historical reasoning.

On the Role of Label Noise in the Feature Learning Process

Deep learning with noisy labels presents significant challenges. In this work, we theoretically characterize the role of label noise from a feature learning perspective. Specifically, we consider a signal-noise data distribution, where each sample comprises a label-dependent signal and label-independent noise, and rigorously analyze the training dynamics of a two-layer convolutional neural network under this data setup, along with the presence of label noise. Our analysis identifies two key stages. In Stage I, the model perfectly fits all the clean samples (i.e., samples without label noise) while ignoring the noisy ones (i.e., samples with noisy labels). During this stage, the model learns the signal from the clean samples, which generalizes well on unseen data. In Stage II, as the training loss converges, the gradient in the direction of noise surpasses that of the signal, leading to overfitting on noisy samples. Eventually, the model memorizes the noise present in the noisy samples and degrades its generalization ability. Furthermore, our analysis provides a theoretical basis for two widely used techniques for tackling label noise: early stopping and sample selection. Experiments on both synthetic and real-world setups validate our theory.

New Evidence of the Two-Phase Learning Dynamics of Neural Networks

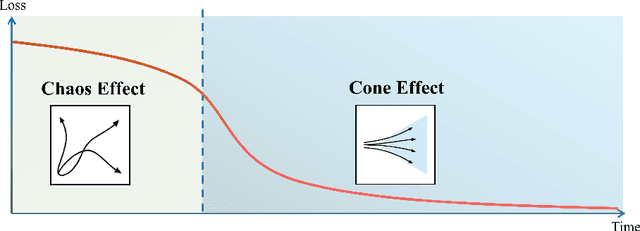
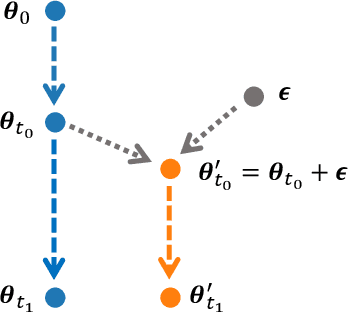
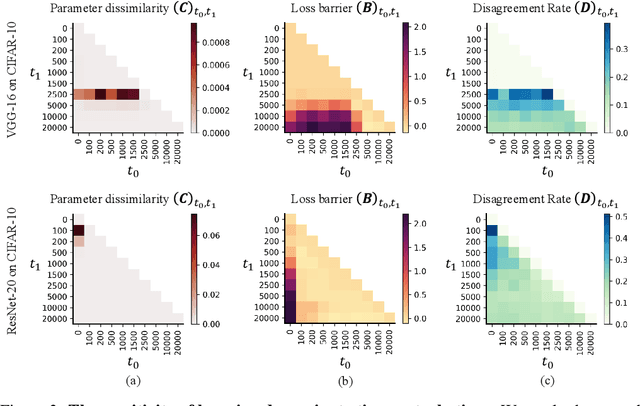
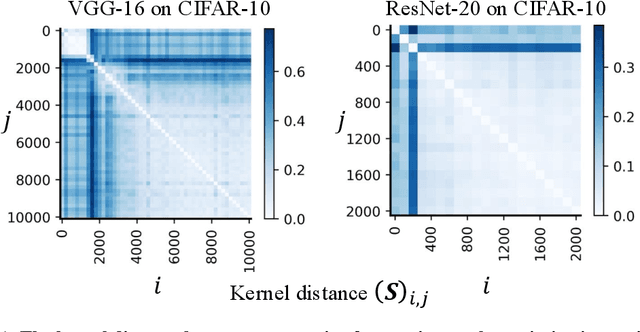
Understanding how deep neural networks learn remains a fundamental challenge in modern machine learning. A growing body of evidence suggests that training dynamics undergo a distinct phase transition, yet our understanding of this transition is still incomplete. In this paper, we introduce an interval-wise perspective that compares network states across a time window, revealing two new phenomena that illuminate the two-phase nature of deep learning. i) \textbf{The Chaos Effect.} By injecting an imperceptibly small parameter perturbation at various stages, we show that the response of the network to the perturbation exhibits a transition from chaotic to stable, suggesting there is an early critical period where the network is highly sensitive to initial conditions; ii) \textbf{The Cone Effect.} Tracking the evolution of the empirical Neural Tangent Kernel (eNTK), we find that after this transition point the model's functional trajectory is confined to a narrow cone-shaped subset: while the kernel continues to change, it gets trapped into a tight angular region. Together, these effects provide a structural, dynamical view of how deep networks transition from sensitive exploration to stable refinement during training.

On the Cone Effect in the Learning Dynamics

Understanding the learning dynamics of neural networks is a central topic in the deep learning community. In this paper, we take an empirical perspective to study the learning dynamics of neural networks in real-world settings. Specifically, we investigate the evolution process of the empirical Neural Tangent Kernel (eNTK) during training. Our key findings reveal a two-phase learning process: i) in Phase I, the eNTK evolves significantly, signaling the rich regime, and ii) in Phase II, the eNTK keeps evolving but is constrained in a narrow space, a phenomenon we term the cone effect. This two-phase framework builds on the hypothesis proposed by Fort et al. (2020), but we uniquely identify the cone effect in Phase II, demonstrating its significant performance advantages over fully linearized training.

The Sharpness Disparity Principle in Transformers for Accelerating Language Model Pre-Training

Transformers consist of diverse building blocks, such as embedding layers, normalization layers, self-attention mechanisms, and point-wise feedforward networks. Thus, understanding the differences and interactions among these blocks is important. In this paper, we uncover a clear Sharpness Disparity across these blocks, which emerges early in training and intriguingly persists throughout the training process. Motivated by this finding, we propose Blockwise Learning Rate (LR), a strategy that tailors the LR to each block's sharpness, accelerating large language model (LLM) pre-training. By integrating Blockwise LR into AdamW, we consistently achieve lower terminal loss and nearly $2\times$ speedup compared to vanilla AdamW. We demonstrate this acceleration across GPT-2 and LLaMA, with model sizes ranging from 0.12B to 1.1B and datasets of OpenWebText and MiniPile. Finally, we incorporate Blockwise LR into Adam-mini (Zhang et al., 2024), a recently proposed memory-efficient variant of Adam, achieving a combined $2\times$ speedup and $2\times$ memory saving. These results underscore the potential of exploiting the sharpness disparity to improve LLM training.

Sharpness-Aware Minimization Efficiently Selects Flatter Minima Late in Training

Sharpness-Aware Minimization (SAM) has substantially improved the generalization of neural networks under various settings. Despite the success, its effectiveness remains poorly understood. In this work, we discover an intriguing phenomenon in the training dynamics of SAM, shedding lights on understanding its implicit bias towards flatter minima over Stochastic Gradient Descent (SGD). Specifically, we find that SAM efficiently selects flatter minima late in training. Remarkably, even a few epochs of SAM applied at the end of training yield nearly the same generalization and solution sharpness as full SAM training. Subsequently, we delve deeper into the underlying mechanism behind this phenomenon. Theoretically, we identify two phases in the learning dynamics after applying SAM late in training: i) SAM first escapes the minimum found by SGD exponentially fast; and ii) then rapidly converges to a flatter minimum within the same valley. Furthermore, we empirically investigate the role of SAM during the early training phase. We conjecture that the optimization method chosen in the late phase is more crucial in shaping the final solution's properties. Based on this viewpoint, we extend our findings from SAM to Adversarial Training.

On the Optimization and Generalization of Two-layer Transformers with Sign Gradient Descent

The Adam optimizer is widely used for transformer optimization in practice, which makes understanding the underlying optimization mechanisms an important problem. However, due to the Adam's complexity, theoretical analysis of how it optimizes transformers remains a challenging task. Fortunately, Sign Gradient Descent (SignGD) serves as an effective surrogate for Adam. Despite its simplicity, theoretical understanding of how SignGD optimizes transformers still lags behind. In this work, we study how SignGD optimizes a two-layer transformer -- consisting of a softmax attention layer with trainable query-key parameterization followed by a linear layer -- on a linearly separable noisy dataset. We identify four stages in the training dynamics, each exhibiting intriguing behaviors. Based on the training dynamics, we prove the fast convergence but poor generalization of the learned transformer on the noisy dataset. We also show that Adam behaves similarly to SignGD in terms of both optimization and generalization in this setting. Additionally, we find that the poor generalization of SignGD is not solely due to data noise, suggesting that both SignGD and Adam requires high-quality data for real-world tasks. Finally, experiments on synthetic and real-world datasets empirically support our theoretical results.

Cross-Task Linearity Emerges in the Pretraining-Finetuning Paradigm

The pretraining-finetuning paradigm has become the prevailing trend in modern deep learning. In this work, we discover an intriguing linear phenomenon in models that are initialized from a common pretrained checkpoint and finetuned on different tasks, termed as Cross-Task Linearity (CTL). Specifically, if we linearly interpolate the weights of two finetuned models, the features in the weight-interpolated model are approximately equal to the linear interpolation of features in two finetuned models at each layer. Such cross-task linearity has not been noted in peer literature. We provide comprehensive empirical evidence supporting that CTL consistently occurs for finetuned models that start from the same pretrained checkpoint. We conjecture that in the pretraining-finetuning paradigm, neural networks essentially function as linear maps, mapping from the parameter space to the feature space. Based on this viewpoint, our study unveils novel insights into explaining model merging/editing, particularly by translating operations from the parameter space to the feature space. Furthermore, we delve deeper into the underlying factors for the emergence of CTL, emphasizing the impact of pretraining.

Going Beyond Neural Network Feature Similarity: The Network Feature Complexity and Its Interpretation Using Category Theory

The behavior of neural networks still remains opaque, and a recently widely noted phenomenon is that networks often achieve similar performance when initialized with different random parameters. This phenomenon has attracted significant attention in measuring the similarity between features learned by distinct networks. However, feature similarity could be vague in describing the same feature since equivalent features hardly exist. In this paper, we expand the concept of equivalent feature and provide the definition of what we call functionally equivalent features. These features produce equivalent output under certain transformations. Using this definition, we aim to derive a more intrinsic metric for the so-called feature complexity regarding the redundancy of features learned by a neural network at each layer. We offer a formal interpretation of our approach through the lens of category theory, a well-developed area in mathematics. To quantify the feature complexity, we further propose an efficient algorithm named Iterative Feature Merging. Our experimental results validate our ideas and theories from various perspectives. We empirically demonstrate that the functionally equivalence widely exists among different features learned by the same neural network and we could reduce the number of parameters of the network without affecting the performance.The IFM shows great potential as a data-agnostic model prune method. We have also drawn several interesting empirical findings regarding the defined feature complexity.

Going Beyond Linear Mode Connectivity: The Layerwise Linear Feature Connectivity

Recent work has revealed many intriguing empirical phenomena in neural network training, despite the poorly understood and highly complex loss landscapes and training dynamics. One of these phenomena, Linear Mode Connectivity (LMC), has gained considerable attention due to the intriguing observation that different solutions can be connected by a linear path in the parameter space while maintaining near-constant training and test losses. In this work, we introduce a stronger notion of linear connectivity, Layerwise Linear Feature Connectivity (LLFC), which says that the feature maps of every layer in different trained networks are also linearly connected. We provide comprehensive empirical evidence for LLFC across a wide range of settings, demonstrating that whenever two trained networks satisfy LMC (via either spawning or permutation methods), they also satisfy LLFC in nearly all the layers. Furthermore, we delve deeper into the underlying factors contributing to LLFC, which reveal new insights into the spawning and permutation approaches. The study of LLFC transcends and advances our understanding of LMC by adopting a feature-learning perspective.