Adapting to Linear Separable Subsets with Large-Margin in Differentially Private Learning

This paper studies the problem of differentially private empirical risk minimization (DP-ERM) for binary linear classification. We obtain an efficient $(\varepsilon,\delta)$-DP algorithm with an empirical zero-one risk bound of $\tilde{O}\left(\frac{1}{\gamma^2\varepsilon n} + \frac{|S_{\mathrm{out}}|}{\gamma n}\right)$ where $n$ is the number of data points, $S_{\mathrm{out}}$ is an arbitrary subset of data one can remove and $\gamma$ is the margin of linear separation of the remaining data points (after $S_{\mathrm{out}}$ is removed). Here, $\tilde{O}(\cdot)$ hides only logarithmic terms. In the agnostic case, we improve the existing results when the number of outliers is small. Our algorithm is highly adaptive because it does not require knowing the margin parameter $\gamma$ or outlier subset $S_{\mathrm{out}}$. We also derive a utility bound for the advanced private hyperparameter tuning algorithm.

Adaptive Estimation and Learning under Temporal Distribution Shift

In this paper, we study the problem of estimation and learning under temporal distribution shift. Consider an observation sequence of length $n$, which is a noisy realization of a time-varying groundtruth sequence. Our focus is to develop methods to estimate the groundtruth at the final time-step while providing sharp point-wise estimation error rates. We show that, without prior knowledge on the level of temporal shift, a wavelet soft-thresholding estimator provides an optimal estimation error bound for the groundtruth. Our proposed estimation method generalizes existing researches Mazzetto and Upfal (2023) by establishing a connection between the sequence's non-stationarity level and the sparsity in the wavelet-transformed domain. Our theoretical findings are validated by numerical experiments. Additionally, we applied the estimator to derive sparsity-aware excess risk bounds for binary classification under distribution shift and to develop computationally efficient training objectives. As a final contribution, we draw parallels between our results and the classical signal processing problem of total-variation denoising (Mammen and van de Geer,1997; Tibshirani, 2014), uncovering novel optimal algorithms for such task.

Adapting to Online Distribution Shifts in Deep Learning: A Black-Box Approach

We study the well-motivated problem of online distribution shift in which the data arrive in batches and the distribution of each batch can change arbitrarily over time. Since the shifts can be large or small, abrupt or gradual, the length of the relevant historical data to learn from may vary over time, which poses a major challenge in designing algorithms that can automatically adapt to the best ``attention span'' while remaining computationally efficient. We propose a meta-algorithm that takes any network architecture and any Online Learner (OL) algorithm as input and produces a new algorithm which provably enhances the performance of the given OL under non-stationarity. Our algorithm is efficient (it requires maintaining only $O(\log(T))$ OL instances) and adaptive (it automatically chooses OL instances with the ideal ``attention'' length at every timestamp). Experiments on various real-world datasets across text and image modalities show that our method consistently improves the accuracy of user specified OL algorithms for classification tasks. Key novel algorithmic ingredients include a \emph{multi-resolution instance} design inspired by wavelet theory and a cross-validation-through-time technique. Both could be of independent interest.

Purifying Approximate Differential Privacy with Randomized Post-processing

We propose a framework to convert $(\varepsilon, \delta)$-approximate Differential Privacy (DP) mechanisms into $(\varepsilon, 0)$-pure DP mechanisms, a process we call ``purification''. This algorithmic technique leverages randomized post-processing with calibrated noise to eliminate the $\delta$ parameter while preserving utility. By combining the tighter utility bounds and computational efficiency of approximate DP mechanisms with the stronger guarantees of pure DP, our approach achieves the best of both worlds. We illustrate the applicability of this framework in various settings, including Differentially Private Empirical Risk Minimization (DP-ERM), data-dependent DP mechanisms such as Propose-Test-Release (PTR), and query release tasks. To the best of our knowledge, this is the first work to provide a systematic method for transforming approximate DP into pure DP while maintaining competitive accuracy and computational efficiency.

Dynamic Pricing with Adversarially-Censored Demands

We study an online dynamic pricing problem where the potential demand at each time period $t=1,2,\ldots, T$ is stochastic and dependent on the price. However, a perishable inventory is imposed at the beginning of each time $t$, censoring the potential demand if it exceeds the inventory level. To address this problem, we introduce a pricing algorithm based on the optimistic estimates of derivatives. We show that our algorithm achieves $\tilde{O}(\sqrt{T})$ optimal regret even with adversarial inventory series. Our findings advance the state-of-the-art in online decision-making problems with censored feedback, offering a theoretically optimal solution against adversarial observations.

Joint Pricing and Resource Allocation: An Optimal Online-Learning Approach

We study an online learning problem on dynamic pricing and resource allocation, where we make joint pricing and inventory decisions to maximize the overall net profit. We consider the stochastic dependence of demands on the price, which complicates the resource allocation process and introduces significant non-convexity and non-smoothness to the problem. To solve this problem, we develop an efficient algorithm that utilizes a "Lower-Confidence Bound (LCB)" meta-strategy over multiple OCO agents. Our algorithm achieves $\tilde{O}(\sqrt{Tmn})$ regret (for $m$ suppliers and $n$ consumers), which is optimal with respect to the time horizon $T$. Our results illustrate an effective integration of statistical learning methodologies with complex operations research problems.

A Proximal Operator for Inducing 2:4-Sparsity

Recent hardware advancements in AI Accelerators and GPUs allow to efficiently compute sparse matrix multiplications, especially when 2 out of 4 consecutive weights are set to zero. However, this so-called 2:4 sparsity usually comes at a decreased accuracy of the model. We derive a regularizer that exploits the local correlation of features to find better sparsity masks in trained models. We minimize the regularizer jointly with a local squared loss by deriving the proximal operator for which we show that it has an efficient solution in the 2:4-sparse case. After optimizing the mask, we use maskedgradient updates to further minimize the local squared loss. We illustrate our method on toy problems and apply it to pruning entire large language models up to 70B parameters. On models up to 13B we improve over previous state of the art algorithms, whilst on 70B models we match their performance.

No-Regret Linear Bandits under Gap-Adjusted Misspecification

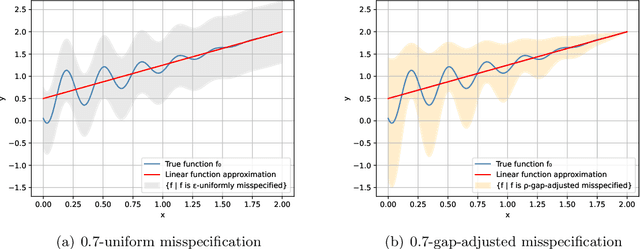
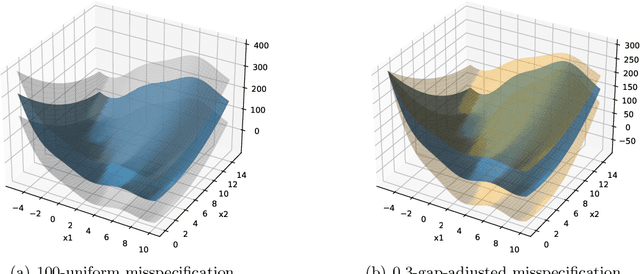
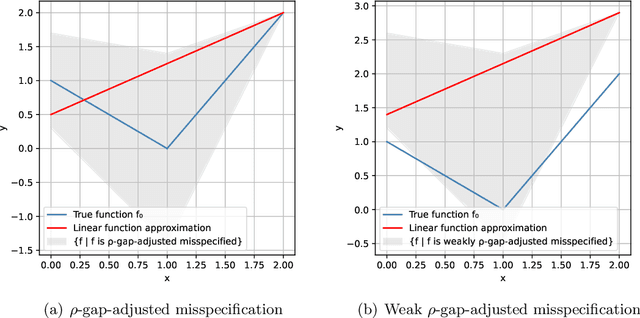
This work studies linear bandits under a new notion of gap-adjusted misspecification and is an extension of Liu et al. (2023). When the underlying reward function is not linear, existing linear bandits work usually relies on a uniform misspecification parameter $\epsilon$ that measures the sup-norm error of the best linear approximation. This results in an unavoidable linear regret whenever $\epsilon > 0$. We propose a more natural model of misspecification which only requires the approximation error at each input $x$ to be proportional to the suboptimality gap at $x$. It captures the intuition that, for optimization problems, near-optimal regions should matter more and we can tolerate larger approximation errors in suboptimal regions. Quite surprisingly, we show that the classical LinUCB algorithm -- designed for the realizable case -- is automatically robust against such $\rho$-gap-adjusted misspecification with parameter $\rho$ diminishing at $O(1/(d \sqrt{\log T}))$. It achieves a near-optimal $O(\sqrt{T})$ regret for problems that the best-known regret is almost linear in time horizon $T$. We further advance this frontier by presenting a novel phased elimination-based algorithm whose gap-adjusted misspecification parameter $\rho = O(1/\sqrt{d})$ does not scale with $T$. This algorithm attains optimal $O(\sqrt{T})$ regret and is deployment-efficient, requiring only $\log T$ batches of exploration. It also enjoys an adaptive $O(\log T)$ regret when a constant suboptimality gap exists. Technically, our proof relies on a novel self-bounding argument that bounds the part of the regret due to misspecification by the regret itself, and a new inductive lemma that limits the misspecification error within the suboptimality gap for all valid actions in each batch selected by G-optimal design.

On the Statistical Complexity for Offline and Low-Adaptive Reinforcement Learning with Structures

This article reviews the recent advances on the statistical foundation of reinforcement learning (RL) in the offline and low-adaptive settings. We will start by arguing why offline RL is the appropriate model for almost any real-life ML problems, even if they have nothing to do with the recent AI breakthroughs that use RL. Then we will zoom into two fundamental problems of offline RL: offline policy evaluation (OPE) and offline policy learning (OPL). It may be surprising to people that tight bounds for these problems were not known even for tabular and linear cases until recently. We delineate the differences between worst-case minimax bounds and instance-dependent bounds. We also cover key algorithmic ideas and proof techniques behind near-optimal instance-dependent methods in OPE and OPL. Finally, we discuss the limitations of offline RL and review a burgeoning problem of \emph{low-adaptive exploration} which addresses these limitations by providing a sweet middle ground between offline and online RL.

SoK: Watermarking for AI-Generated Content

As the outputs of generative AI (GenAI) techniques improve in quality, it becomes increasingly challenging to distinguish them from human-created content. Watermarking schemes are a promising approach to address the problem of distinguishing between AI and human-generated content. These schemes embed hidden signals within AI-generated content to enable reliable detection. While watermarking is not a silver bullet for addressing all risks associated with GenAI, it can play a crucial role in enhancing AI safety and trustworthiness by combating misinformation and deception. This paper presents a comprehensive overview of watermarking techniques for GenAI, beginning with the need for watermarking from historical and regulatory perspectives. We formalize the definitions and desired properties of watermarking schemes and examine the key objectives and threat models for existing approaches. Practical evaluation strategies are also explored, providing insights into the development of robust watermarking techniques capable of resisting various attacks. Additionally, we review recent representative works, highlight open challenges, and discuss potential directions for this emerging field. By offering a thorough understanding of watermarking in GenAI, this work aims to guide researchers in advancing watermarking methods and applications, and support policymakers in addressing the broader implications of GenAI.