Dheeraj Baby
Adaptive Estimation and Learning under Temporal Distribution Shift
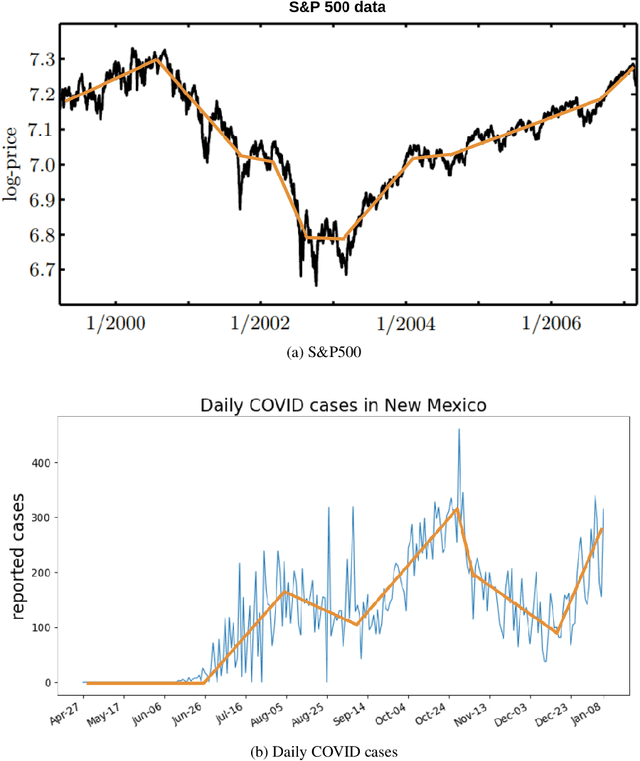
May 21, 2025Abstract:In this paper, we study the problem of estimation and learning under temporal distribution shift. Consider an observation sequence of length $n$, which is a noisy realization of a time-varying groundtruth sequence. Our focus is to develop methods to estimate the groundtruth at the final time-step while providing sharp point-wise estimation error rates. We show that, without prior knowledge on the level of temporal shift, a wavelet soft-thresholding estimator provides an optimal estimation error bound for the groundtruth. Our proposed estimation method generalizes existing researches Mazzetto and Upfal (2023) by establishing a connection between the sequence's non-stationarity level and the sparsity in the wavelet-transformed domain. Our theoretical findings are validated by numerical experiments. Additionally, we applied the estimator to derive sparsity-aware excess risk bounds for binary classification under distribution shift and to develop computationally efficient training objectives. As a final contribution, we draw parallels between our results and the classical signal processing problem of total-variation denoising (Mammen and van de Geer,1997; Tibshirani, 2014), uncovering novel optimal algorithms for such task.
Adapting to Online Distribution Shifts in Deep Learning: A Black-Box Approach
Apr 09, 2025Abstract:We study the well-motivated problem of online distribution shift in which the data arrive in batches and the distribution of each batch can change arbitrarily over time. Since the shifts can be large or small, abrupt or gradual, the length of the relevant historical data to learn from may vary over time, which poses a major challenge in designing algorithms that can automatically adapt to the best ``attention span'' while remaining computationally efficient. We propose a meta-algorithm that takes any network architecture and any Online Learner (OL) algorithm as input and produces a new algorithm which provably enhances the performance of the given OL under non-stationarity. Our algorithm is efficient (it requires maintaining only $O(\log(T))$ OL instances) and adaptive (it automatically chooses OL instances with the ideal ``attention'' length at every timestamp). Experiments on various real-world datasets across text and image modalities show that our method consistently improves the accuracy of user specified OL algorithms for classification tasks. Key novel algorithmic ingredients include a \emph{multi-resolution instance} design inspired by wavelet theory and a cross-validation-through-time technique. Both could be of independent interest.
Online Matrix Completion: A Collaborative Approach with Hott Items
Aug 11, 2024
Abstract:We investigate the low rank matrix completion problem in an online setting with ${M}$ users, ${N}$ items, ${T}$ rounds, and an unknown rank-$r$ reward matrix ${R}\in \mathbb{R}^{{M}\times {N}}$. This problem has been well-studied in the literature and has several applications in practice. In each round, we recommend ${S}$ carefully chosen distinct items to every user and observe noisy rewards. In the regime where ${M},{N} >> {T}$, we propose two distinct computationally efficient algorithms for recommending items to users and analyze them under the benign \emph{hott items} assumption.1) First, for ${S}=1$, under additional incoherence/smoothness assumptions on ${R}$, we propose the phased algorithm \textsc{PhasedClusterElim}. Our algorithm obtains a near-optimal per-user regret of $\tilde{O}({N}{M}^{-1}(\Delta^{-1}+\Delta_{{hott}}^{-2}))$ where $\Delta_{{hott}},\Delta$ are problem-dependent gap parameters with $\Delta_{{hott}} >> \Delta$ almost always. 2) Second, we consider a simplified setting with ${S}=r$ where we make significantly milder assumptions on ${R}$. Here, we introduce another phased algorithm, \textsc{DeterminantElim}, to derive a regret guarantee of $\widetilde{O}({N}{M}^{-1/r}\Delta_{det}^{-1}))$ where $\Delta_{{det}}$ is another problem-dependent gap. Both algorithms crucially use collaboration among users to jointly eliminate sub-optimal items for groups of users successively in phases, but with distinctive and novel approaches.
Online Feature Updates Improve Online (Generalized) Label Shift Adaptation
Feb 05, 2024Abstract:This paper addresses the prevalent issue of label shift in an online setting with missing labels, where data distributions change over time and obtaining timely labels is challenging. While existing methods primarily focus on adjusting or updating the final layer of a pre-trained classifier, we explore the untapped potential of enhancing feature representations using unlabeled data at test-time. Our novel method, Online Label Shift adaptation with Online Feature Updates (OLS-OFU), leverages self-supervised learning to refine the feature extraction process, thereby improving the prediction model. Theoretical analyses confirm that OLS-OFU reduces algorithmic regret by capitalizing on self-supervised learning for feature refinement. Empirical studies on various datasets, under both online label shift and generalized label shift conditions, underscore the effectiveness and robustness of OLS-OFU, especially in cases of domain shifts.
Near Optimal Heteroscedastic Regression with Symbiotic Learning
Jul 01, 2023Abstract:We consider the problem of heteroscedastic linear regression, where, given $n$ samples $(\mathbf{x}_i, y_i)$ from $y_i = \langle \mathbf{w}^{*}, \mathbf{x}_i \rangle + \epsilon_i \cdot \langle \mathbf{f}^{*}, \mathbf{x}_i \rangle$ with $\mathbf{x}_i \sim N(0,\mathbf{I})$, $\epsilon_i \sim N(0,1)$, we aim to estimate $\mathbf{w}^{*}$. Beyond classical applications of such models in statistics, econometrics, time series analysis etc., it is also particularly relevant in machine learning when data is collected from multiple sources of varying but apriori unknown quality. Our work shows that we can estimate $\mathbf{w}^{*}$ in squared norm up to an error of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2 \cdot \left(\frac{1}{n} + \left(\frac{d}{n}\right)^2\right)\right)$ and prove a matching lower bound (upto log factors). This represents a substantial improvement upon the previous best known upper bound of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2\cdot \frac{d}{n}\right)$. Our algorithm is an alternating minimization procedure with two key subroutines 1. An adaptation of the classical weighted least squares heuristic to estimate $\mathbf{w}^{*}$, for which we provide the first non-asymptotic guarantee. 2. A nonconvex pseudogradient descent procedure for estimating $\mathbf{f}^{*}$ inspired by phase retrieval. As corollaries, we obtain fast non-asymptotic rates for two important problems, linear regression with multiplicative noise and phase retrieval with multiplicative noise, both of which are of independent interest. Beyond this, the proof of our lower bound, which involves a novel adaptation of LeCam's method for handling infinite mutual information quantities (thereby preventing a direct application of standard techniques like Fano's method), could also be of broader interest for establishing lower bounds for other heteroscedastic or heavy-tailed statistical problems.
Online Label Shift: Optimal Dynamic Regret meets Practical Algorithms
May 31, 2023Abstract:This paper focuses on supervised and unsupervised online label shift, where the class marginals $Q(y)$ varies but the class-conditionals $Q(x|y)$ remain invariant. In the unsupervised setting, our goal is to adapt a learner, trained on some offline labeled data, to changing label distributions given unlabeled online data. In the supervised setting, we must both learn a classifier and adapt to the dynamically evolving class marginals given only labeled online data. We develop novel algorithms that reduce the adaptation problem to online regression and guarantee optimal dynamic regret without any prior knowledge of the extent of drift in the label distribution. Our solution is based on bootstrapping the estimates of \emph{online regression oracles} that track the drifting proportions. Experiments across numerous simulated and real-world online label shift scenarios demonstrate the superior performance of our proposed approaches, often achieving 1-3\% improvement in accuracy while being sample and computationally efficient. Code is publicly available at https://github.com/acmi-lab/OnlineLabelShift.
Optimal Dynamic Regret in LQR Control
Jun 18, 2022


Abstract:We consider the problem of nonstochastic control with a sequence of quadratic losses, i.e., LQR control. We provide an efficient online algorithm that achieves an optimal dynamic (policy) regret of $\tilde{O}(\text{max}\{n^{1/3} \mathcal{TV}(M_{1:n})^{2/3}, 1\})$, where $\mathcal{TV}(M_{1:n})$ is the total variation of any oracle sequence of Disturbance Action policies parameterized by $M_1,...,M_n$ -- chosen in hindsight to cater to unknown nonstationarity. The rate improves the best known rate of $\tilde{O}(\sqrt{n (\mathcal{TV}(M_{1:n})+1)} )$ for general convex losses and we prove that it is information-theoretically optimal for LQR. Main technical components include the reduction of LQR to online linear regression with delayed feedback due to Foster and Simchowitz (2020), as well as a new proper learning algorithm with an optimal $\tilde{O}(n^{1/3})$ dynamic regret on a family of ``minibatched'' quadratic losses, which could be of independent interest.
Second Order Path Variationals in Non-Stationary Online Learning
May 04, 2022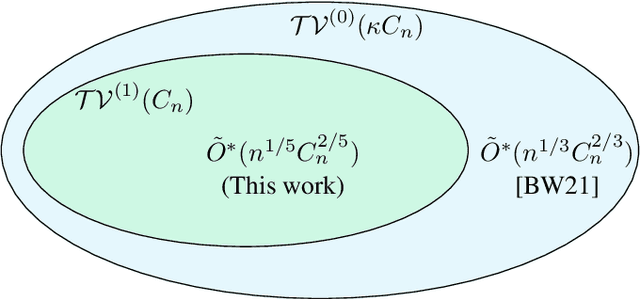


Abstract:We consider the problem of universal dynamic regret minimization under exp-concave and smooth losses. We show that appropriately designed Strongly Adaptive algorithms achieve a dynamic regret of $\tilde O(d^2 n^{1/5} C_n^{2/5} \vee d^2)$, where $n$ is the time horizon and $C_n$ a path variational based on second order differences of the comparator sequence. Such a path variational naturally encodes comparator sequences that are piecewise linear -- a powerful family that tracks a variety of non-stationarity patterns in practice (Kim et al, 2009). The aforementioned dynamic regret rate is shown to be optimal modulo dimension dependencies and poly-logarithmic factors of $n$. Our proof techniques rely on analysing the KKT conditions of the offline oracle and requires several non-trivial generalizations of the ideas in Baby and Wang, 2021, where the latter work only leads to a slower dynamic regret rate of $\tilde O(d^{2.5}n^{1/3}C_n^{2/3} \vee d^{2.5})$ for the current problem.
Optimal Dynamic Regret in Proper Online Learning with Strongly Convex Losses and Beyond
Jan 21, 2022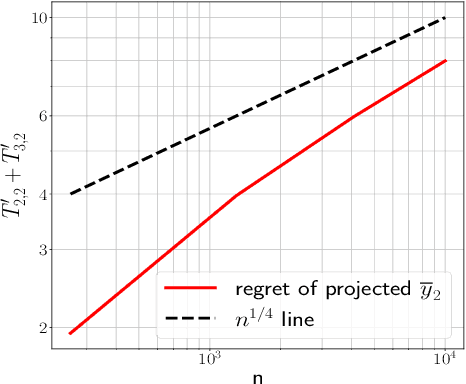


Abstract:We study the framework of universal dynamic regret minimization with strongly convex losses. We answer an open problem in Baby and Wang 2021 by showing that in a proper learning setup, Strongly Adaptive algorithms can achieve the near optimal dynamic regret of $\tilde O(d^{1/3} n^{1/3}\text{TV}[u_{1:n}]^{2/3} \vee d)$ against any comparator sequence $u_1,\ldots,u_n$ simultaneously, where $n$ is the time horizon and $\text{TV}[u_{1:n}]$ is the Total Variation of comparator. These results are facilitated by exploiting a number of new structures imposed by the KKT conditions that were not considered in Baby and Wang 2021 which also lead to other improvements over their results such as: (a) handling non-smooth losses and (b) improving the dimension dependence on regret. Further, we also derive near optimal dynamic regret rates for the special case of proper online learning with exp-concave losses and an $L_\infty$ constrained decision set.
Dynamic Regret for Strongly Adaptive Methods and Optimality of Online KRR
Nov 22, 2021
Abstract:We consider the framework of non-stationary Online Convex Optimization where a learner seeks to control its dynamic regret against an arbitrary sequence of comparators. When the loss functions are strongly convex or exp-concave, we demonstrate that Strongly Adaptive (SA) algorithms can be viewed as a principled way of controlling dynamic regret in terms of path variation $V_T$ of the comparator sequence. Specifically, we show that SA algorithms enjoy $\tilde O(\sqrt{TV_T} \vee \log T)$ and $\tilde O(\sqrt{dTV_T} \vee d\log T)$ dynamic regret for strongly convex and exp-concave losses respectively without apriori knowledge of $V_T$. The versatility of the principled approach is further demonstrated by the novel results in the setting of learning against bounded linear predictors and online regression with Gaussian kernels. Under a related setting, the second component of the paper addresses an open question posed by Zhdanov and Kalnishkan (2010) that concerns online kernel regression with squared error losses. We derive a new lower bound on a certain penalized regret which establishes the near minimax optimality of online Kernel Ridge Regression (KRR). Our lower bound can be viewed as an RKHS extension to the lower bound derived in Vovk (2001) for online linear regression in finite dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge