Context-lumpable stochastic bandits

We consider a contextual bandit problem with $S $ contexts and $A $ actions. In each round $t=1,2,\dots$ the learner observes a random context and chooses an action based on its past experience. The learner then observes a random reward whose mean is a function of the context and the action for the round. Under the assumption that the contexts can be lumped into $r\le \min\{S ,A \}$ groups such that the mean reward for the various actions is the same for any two contexts that are in the same group, we give an algorithm that outputs an $\epsilon$-optimal policy after using at most $\widetilde O(r (S +A )/\epsilon^2)$ samples with high probability and provide a matching $\widetilde\Omega(r (S +A )/\epsilon^2)$ lower bound. In the regret minimization setting, we give an algorithm whose cumulative regret up to time $T$ is bounded by $\widetilde O(\sqrt{r^3(S +A )T})$. To the best of our knowledge, we are the first to show the near-optimal sample complexity in the PAC setting and $\widetilde O(\sqrt{{poly}(r)(S+K)T})$ minimax regret in the online setting for this problem. We also show our algorithms can be applied to more general low-rank bandits and get improved regret bounds in some scenarios.

Non-stationary Bandits and Meta-Learning with a Small Set of Optimal Arms

We study a sequential decision problem where the learner faces a sequence of $K$-armed stochastic bandit tasks. The tasks may be designed by an adversary, but the adversary is constrained to choose the optimal arm of each task in a smaller (but unknown) subset of $M$ arms. The task boundaries might be known (the bandit meta-learning setting), or unknown (the non-stationary bandit setting), and the number of tasks $N$ as well as the total number of rounds $T$ are known ($N$ could be unknown in the meta-learning setting). We design an algorithm based on a reduction to bandit submodular maximization, and show that its regret in both settings is smaller than the simple baseline of $\tilde{O}(\sqrt{KNT})$ that can be obtained by using standard algorithms designed for non-stationary bandit problems. For the bandit meta-learning problem with fixed task length $\tau$, we show that the regret of the algorithm is bounded as $\tilde{O}(N\sqrt{M \tau}+N^{2/3})$. Under additional assumptions on the identifiability of the optimal arms in each task, we show a bandit meta-learning algorithm with an improved $\tilde{O}(N\sqrt{M \tau}+N^{1/2})$ regret.

A New Look at Dynamic Regret for Non-Stationary Stochastic Bandits

We study the non-stationary stochastic multi-armed bandit problem, where the reward statistics of each arm may change several times during the course of learning. The performance of a learning algorithm is evaluated in terms of their dynamic regret, which is defined as the difference of the expected cumulative reward of an agent choosing the optimal arm in every round and the cumulative reward of the learning algorithm. One way to measure the hardness of such environments is to consider how many times the identity of the optimal arm can change. We propose a method that achieves, in $K$-armed bandit problems, a near-optimal $\widetilde O(\sqrt{K N(S+1)})$ dynamic regret, where $N$ is the number of rounds and $S$ is the number of times the identity of the optimal arm changes, without prior knowledge of $S$ and $N$. Previous works for this problem obtain regret bounds that scale with the number of changes (or the amount of change) in the reward functions, which can be much larger, or assume prior knowledge of $S$ to achieve similar bounds.

Efficient Local Planning with Linear Function Approximation

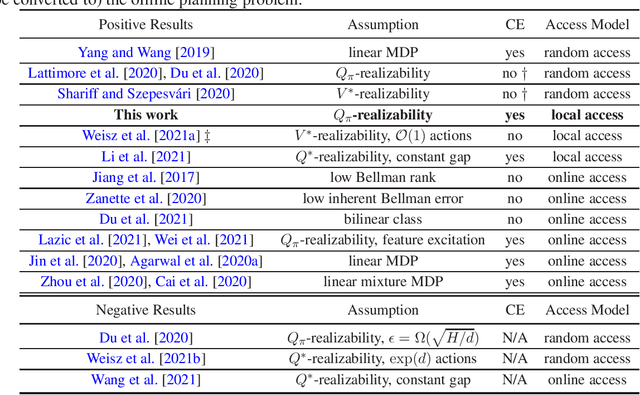
We study query and computationally efficient planning algorithms with linear function approximation and a simulator. We assume that the agent only has local access to the simulator, meaning that the agent can only query the simulator at states that have been visited before. This setting is more practical than many prior works on reinforcement learning with a generative model. We propose an algorithm named confident Monte Carlo least square policy iteration (Confident MC-LSPI) for this setting. Under the assumption that the Q-functions of all deterministic policies are linear in known features of the state-action pairs, we show that our algorithm has polynomial query and computational complexities in the dimension of the features, the effective planning horizon and the targeted sub-optimality, while these complexities are independent of the size of the state space. One technical contribution of our work is the introduction of a novel proof technique that makes use of a virtual policy iteration algorithm. We use this method to leverage existing results on $\ell_\infty$-bounded approximate policy iteration to show that our algorithm can learn the optimal policy for the given initial state even only with local access to the simulator. We believe that this technique can be extended to broader settings beyond this work.

Parameter and Feature Selection in Stochastic Linear Bandits

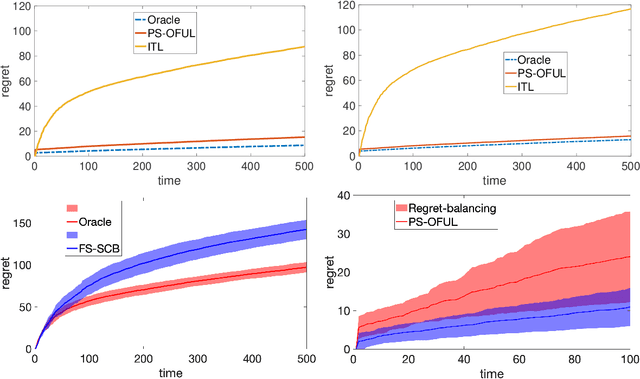
We study two model selection settings in stochastic linear bandits (LB). In the first setting, the reward parameter of the LB problem is arbitrarily selected from $M$ models represented as (possibly) overlapping balls in $\mathbb R^d$. However, the agent only has access to misspecified models, i.e., estimates of the centers and radii of the balls. We refer to this setting as parameter selection. In the second setting, which we refer to as feature selection, the expected reward of the LB problem is in the linear span of at least one of $M$ feature maps (models). For each setting, we develop and analyze an algorithm that is based on a reduction from bandits to full-information problems. This allows us to obtain regret bounds that are not worse (up to a $\sqrt{\log M}$ factor) than the case where the true model is known. Our parameter selection algorithm is OFUL-style and the one for feature selection is based on the SquareCB algorithm. We also show that the regret of our parameter selection algorithm scales logarithmically with model misspecification.

Improved Regret Bound and Experience Replay in Regularized Policy Iteration

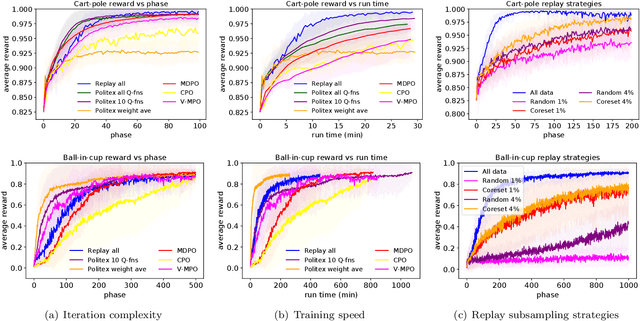
In this work, we study algorithms for learning in infinite-horizon undiscounted Markov decision processes (MDPs) with function approximation. We first show that the regret analysis of the Politex algorithm (a version of regularized policy iteration) can be sharpened from $O(T^{3/4})$ to $O(\sqrt{T})$ under nearly identical assumptions, and instantiate the bound with linear function approximation. Our result provides the first high-probability $O(\sqrt{T})$ regret bound for a computationally efficient algorithm in this setting. The exact implementation of Politex with neural network function approximation is inefficient in terms of memory and computation. Since our analysis suggests that we need to approximate the average of the action-value functions of past policies well, we propose a simple efficient implementation where we train a single Q-function on a replay buffer with past data. We show that this often leads to superior performance over other implementation choices, especially in terms of wall-clock time. Our work also provides a novel theoretical justification for using experience replay within policy iteration algorithms.

Optimization Issues in KL-Constrained Approximate Policy Iteration

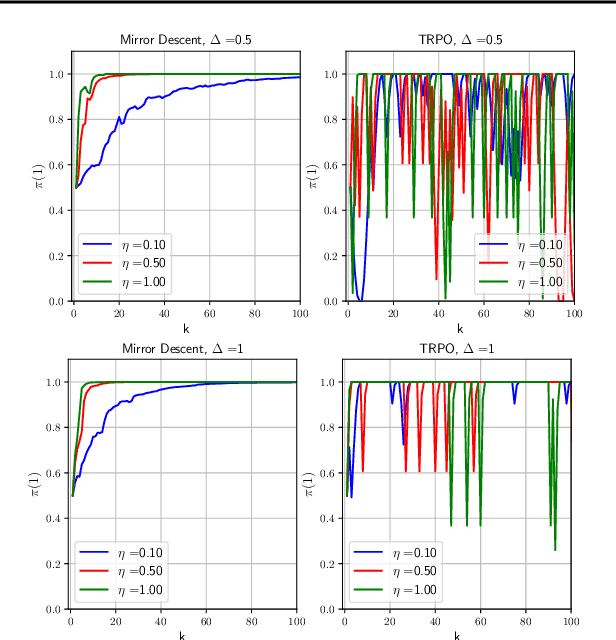
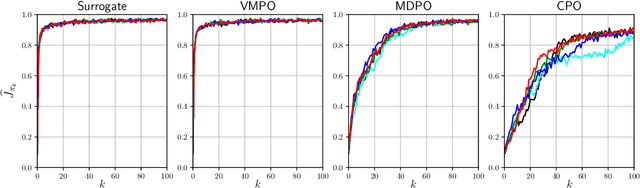
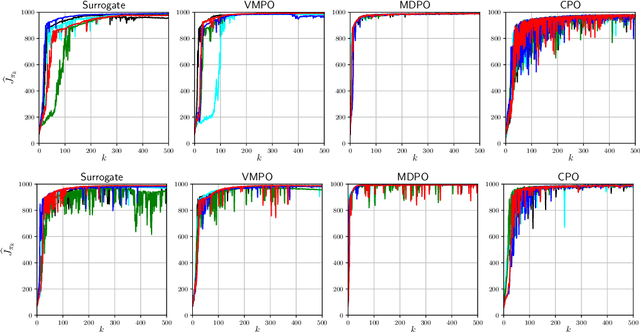
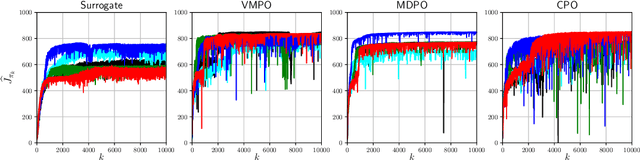
Many reinforcement learning algorithms can be seen as versions of approximate policy iteration (API). While standard API often performs poorly, it has been shown that learning can be stabilized by regularizing each policy update by the KL-divergence to the previous policy. Popular practical algorithms such as TRPO, MPO, and VMPO replace regularization by a constraint on KL-divergence of consecutive policies, arguing that this is easier to implement and tune. In this work, we study this implementation choice in more detail. We compare the use of KL divergence as a constraint vs. as a regularizer, and point out several optimization issues with the widely-used constrained approach. We show that the constrained algorithm is not guaranteed to converge even on simple problem instances where the constrained problem can be solved exactly, and in fact incurs linear expected regret. With approximate implementation using softmax policies, we show that regularization can improve the optimization landscape of the original objective. We demonstrate these issues empirically on several bandit and RL environments.

On Query-efficient Planning in MDPs under Linear Realizability of the Optimal State-value Function

We consider the problem of local planning in fixed-horizon Markov Decision Processes (MDPs) with a generative model under the assumption that the optimal value function lies in the span of a feature map that is accessible through the generative model. As opposed to previous work where linear realizability of all policies was assumed, we consider the significantly relaxed assumption of a single linearly realizable (deterministic) policy. A recent lower bound established that the related problem when the action-value function of the optimal policy is linearly realizable requires an exponential number of queries, either in H (the horizon of the MDP) or d (the dimension of the feature mapping). Their construction crucially relies on having an exponentially large action set. In contrast, in this work, we establish that poly$(H, d)$ learning is possible (with state value function realizability) whenever the action set is small (i.e. O(1)). In particular, we present the TensorPlan algorithm which uses poly$((dH/\delta)^A)$ queries to find a $\delta$-optimal policy relative to any deterministic policy for which the value function is linearly realizable with a parameter from a fixed radius ball around zero. This is the first algorithm to give a polynomial query complexity guarantee using only linear-realizability of a single competing value function. Whether the computation cost is similarly bounded remains an interesting open question. The upper bound is complemented by a lower bound which proves that in the infinite-horizon episodic setting, planners that achieve constant suboptimality need exponentially many queries, either in the dimension or the number of actions.

The Elliptical Potential Lemma Revisited

This note proposes a new proof and new perspectives on the so-called Elliptical Potential Lemma. This result is important in online learning, especially for linear stochastic bandits. The original proof of the result, however short and elegant, does not give much flexibility on the type of potentials considered and we believe that this new interpretation can be of interest for future research in this field.

Regret Balancing for Bandit and RL Model Selection

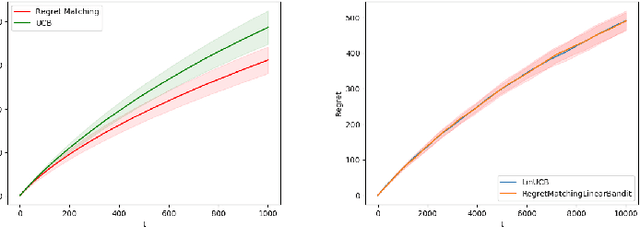
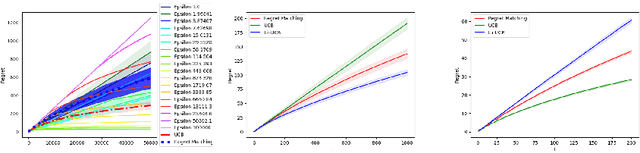
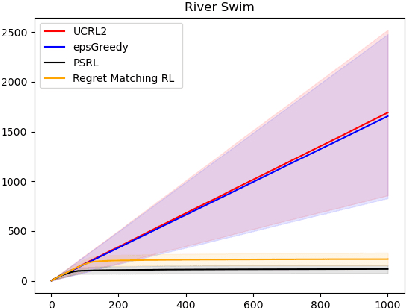
We consider model selection in stochastic bandit and reinforcement learning problems. Given a set of base learning algorithms, an effective model selection strategy adapts to the best learning algorithm in an online fashion. We show that by estimating the regret of each algorithm and playing the algorithms such that all empirical regrets are ensured to be of the same order, the overall regret balancing strategy achieves a regret that is close to the regret of the optimal base algorithm. Our strategy requires an upper bound on the optimal base regret as input, and the performance of the strategy depends on the tightness of the upper bound. We show that having this prior knowledge is necessary in order to achieve a near-optimal regret. Further, we show that any near-optimal model selection strategy implicitly performs a form of regret balancing.