Fast Last-Iterate Convergence of Learning in Games Requires Forgetful Algorithms

Self-play via online learning is one of the premier ways to solve large-scale two-player zero-sum games, both in theory and practice. Particularly popular algorithms include optimistic multiplicative weights update (OMWU) and optimistic gradient-descent-ascent (OGDA). While both algorithms enjoy $O(1/T)$ ergodic convergence to Nash equilibrium in two-player zero-sum games, OMWU offers several advantages including logarithmic dependence on the size of the payoff matrix and $\widetilde{O}(1/T)$ convergence to coarse correlated equilibria even in general-sum games. However, in terms of last-iterate convergence in two-player zero-sum games, an increasingly popular topic in this area, OGDA guarantees that the duality gap shrinks at a rate of $O(1/\sqrt{T})$, while the best existing last-iterate convergence for OMWU depends on some game-dependent constant that could be arbitrarily large. This begs the question: is this potentially slow last-iterate convergence an inherent disadvantage of OMWU, or is the current analysis too loose? Somewhat surprisingly, we show that the former is true. More generally, we prove that a broad class of algorithms that do not forget the past quickly all suffer the same issue: for any arbitrarily small $\delta>0$, there exists a $2\times 2$ matrix game such that the algorithm admits a constant duality gap even after $1/\delta$ rounds. This class of algorithms includes OMWU and other standard optimistic follow-the-regularized-leader algorithms.

Last-Iterate Convergence Properties of Regret-Matching Algorithms in Games

Algorithms based on regret matching, specifically regret matching$^+$ (RM$^+$), and its variants are the most popular approaches for solving large-scale two-player zero-sum games in practice. Unlike algorithms such as optimistic gradient descent ascent, which have strong last-iterate and ergodic convergence properties for zero-sum games, virtually nothing is known about the last-iterate properties of regret-matching algorithms. Given the importance of last-iterate convergence for numerical optimization reasons and relevance as modeling real-word learning in games, in this paper, we study the last-iterate convergence properties of various popular variants of RM$^+$. First, we show numerically that several practical variants such as simultaneous RM$^+$, alternating RM$^+$, and simultaneous predictive RM$^+$, all lack last-iterate convergence guarantees even on a simple $3\times 3$ game. We then prove that recent variants of these algorithms based on a smoothing technique do enjoy last-iterate convergence: we prove that extragradient RM$^{+}$ and smooth Predictive RM$^+$ enjoy asymptotic last-iterate convergence (without a rate) and $1/\sqrt{t}$ best-iterate convergence. Finally, we introduce restarted variants of these algorithms, and show that they enjoy linear-rate last-iterate convergence.

Context-lumpable stochastic bandits

We consider a contextual bandit problem with $S $ contexts and $A $ actions. In each round $t=1,2,\dots$ the learner observes a random context and chooses an action based on its past experience. The learner then observes a random reward whose mean is a function of the context and the action for the round. Under the assumption that the contexts can be lumped into $r\le \min\{S ,A \}$ groups such that the mean reward for the various actions is the same for any two contexts that are in the same group, we give an algorithm that outputs an $\epsilon$-optimal policy after using at most $\widetilde O(r (S +A )/\epsilon^2)$ samples with high probability and provide a matching $\widetilde\Omega(r (S +A )/\epsilon^2)$ lower bound. In the regret minimization setting, we give an algorithm whose cumulative regret up to time $T$ is bounded by $\widetilde O(\sqrt{r^3(S +A )T})$. To the best of our knowledge, we are the first to show the near-optimal sample complexity in the PAC setting and $\widetilde O(\sqrt{{poly}(r)(S+K)T})$ minimax regret in the online setting for this problem. We also show our algorithms can be applied to more general low-rank bandits and get improved regret bounds in some scenarios.

Regret Matching+: (In)Stability and Fast Convergence in Games

Regret Matching+ (RM+) and its variants are important algorithms for solving large-scale games. However, a theoretical understanding of their success in practice is still a mystery. Moreover, recent advances on fast convergence in games are limited to no-regret algorithms such as online mirror descent, which satisfy stability. In this paper, we first give counterexamples showing that RM+ and its predictive version can be unstable, which might cause other players to suffer large regret. We then provide two fixes: restarting and chopping off the positive orthant that RM+ works in. We show that these fixes are sufficient to get $O(T^{1/4})$ individual regret and $O(1)$ social regret in normal-form games via RM+ with predictions. We also apply our stabilizing techniques to clairvoyant updates in the uncoupled learning setting for RM+ and prove desirable results akin to recent works for Clairvoyant online mirror descent. Our experiments show the advantages of our algorithms over vanilla RM+-based algorithms in matrix and extensive-form games.

Practical Knowledge Distillation: Using DNNs to Beat DNNs

For tabular data sets, we explore data and model distillation, as well as data denoising. These techniques improve both gradient-boosting models and a specialized DNN architecture. While gradient boosting is known to outperform DNNs on tabular data, we close the gap for datasets with 100K+ rows and give DNNs an advantage on small data sets. We extend these results with input-data distillation and optimized ensembling to help DNN performance match or exceed that of gradient boosting. As a theoretical justification of our practical method, we prove its equivalence to classical cross-entropy knowledge distillation. We also qualitatively explain the superiority of DNN ensembles over XGBoost on small data sets. For an industry end-to-end real-time ML platform with 4M production inferences per second, we develop a model-training workflow based on data sampling that distills ensembles of models into a single gradient-boosting model favored for high-performance real-time inference, without performance loss. Empirical evaluation shows that the proposed combination of methods consistently improves model accuracy over prior best models across several production applications deployed worldwide.

Near-Optimal No-Regret Learning for General Convex Games

A recent line of work has established uncoupled learning dynamics such that, when employed by all players in a game, each player's \emph{regret} after $T$ repetitions grows polylogarithmically in $T$, an exponential improvement over the traditional guarantees within the no-regret framework. However, so far these results have only been limited to certain classes of games with structured strategy spaces -- such as normal-form and extensive-form games. The question as to whether $O(\text{polylog} T)$ regret bounds can be obtained for general convex and compact strategy sets -- which occur in many fundamental models in economics and multiagent systems -- while retaining efficient strategy updates is an important question. In this paper, we answer this in the positive by establishing the first uncoupled learning algorithm with $O(\log T)$ per-player regret in general \emph{convex games}, that is, games with concave utility functions supported on arbitrary convex and compact strategy sets. Our learning dynamics are based on an instantiation of optimistic follow-the-regularized-leader over an appropriately \emph{lifted} space using a \emph{self-concordant regularizer} that is, peculiarly, not a barrier for the feasible region. Further, our learning dynamics are efficiently implementable given access to a proximal oracle for the convex strategy set, leading to $O(\log\log T)$ per-iteration complexity; we also give extensions when access to only a \emph{linear} optimization oracle is assumed. Finally, we adapt our dynamics to guarantee $O(\sqrt{T})$ regret in the adversarial regime. Even in those special cases where prior results apply, our algorithm improves over the state-of-the-art regret bounds either in terms of the dependence on the number of iterations or on the dimension of the strategy sets.

Uncoupled Learning Dynamics with $O(\log T)$ Swap Regret in Multiplayer Games

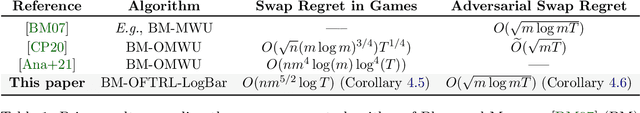
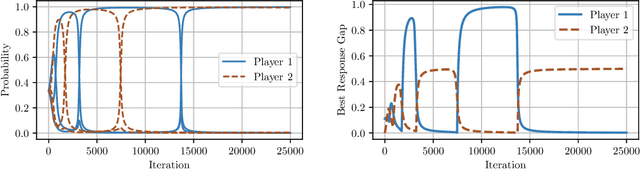
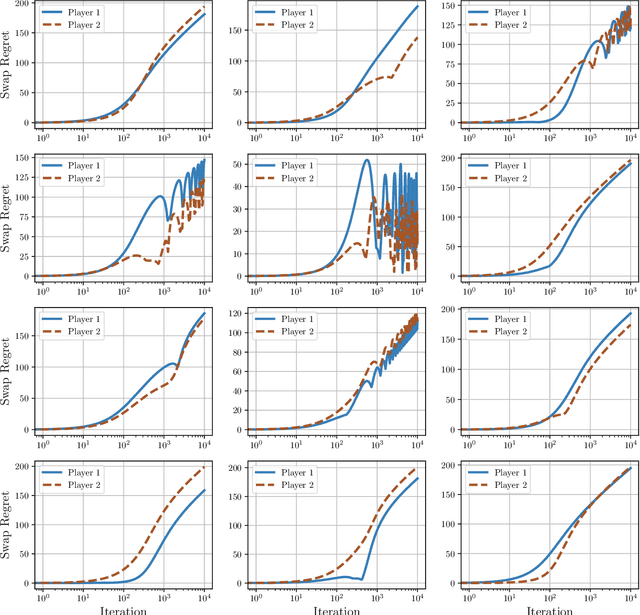
In this paper we establish efficient and \emph{uncoupled} learning dynamics so that, when employed by all players in a general-sum multiplayer game, the \emph{swap regret} of each player after $T$ repetitions of the game is bounded by $O(\log T)$, improving over the prior best bounds of $O(\log^4 (T))$. At the same time, we guarantee optimal $O(\sqrt{T})$ swap regret in the adversarial regime as well. To obtain these results, our primary contribution is to show that when all players follow our dynamics with a \emph{time-invariant} learning rate, the \emph{second-order path lengths} of the dynamics up to time $T$ are bounded by $O(\log T)$, a fundamental property which could have further implications beyond near-optimally bounding the (swap) regret. Our proposed learning dynamics combine in a novel way \emph{optimistic} regularized learning with the use of \emph{self-concordant barriers}. Further, our analysis is remarkably simple, bypassing the cumbersome framework of higher-order smoothness recently developed by Daskalakis, Fishelson, and Golowich (NeurIPS'21).

Kernelized Multiplicative Weights for 0/1-Polyhedral Games: Bridging the Gap Between Learning in Extensive-Form and Normal-Form Games

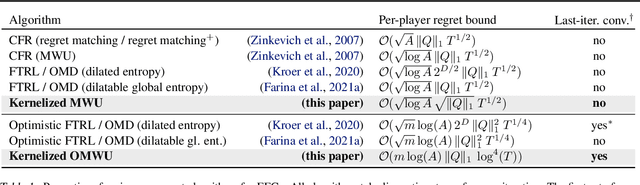
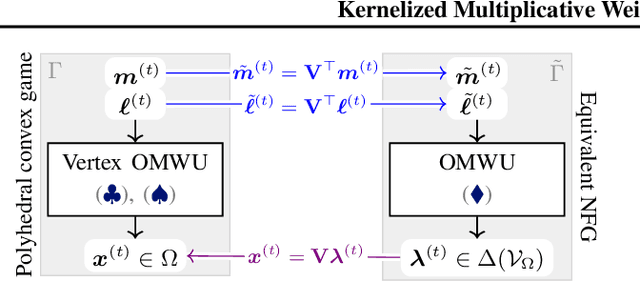
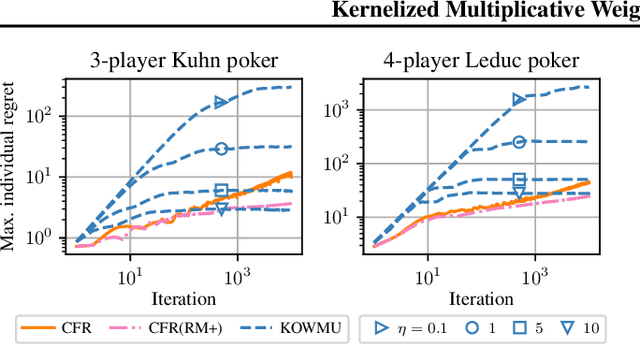
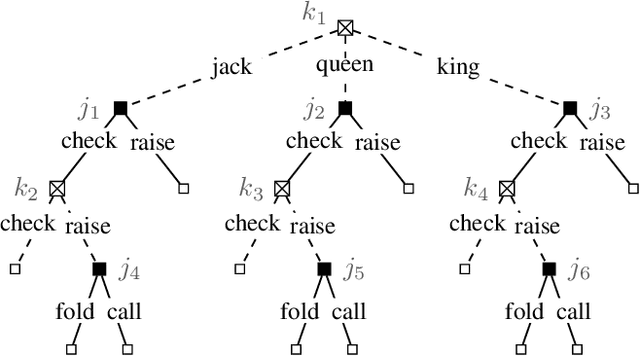
While extensive-form games (EFGs) can be converted into normal-form games (NFGs), doing so comes at the cost of an exponential blowup of the strategy space. So, progress on NFGs and EFGs has historically followed separate tracks, with the EFG community often having to catch up with advances (e.g., last-iterate convergence and predictive regret bounds) from the larger NFG community. In this paper we show that the Optimistic Multiplicative Weights Update (OMWU) algorithm -- the premier learning algorithm for NFGs -- can be simulated on the normal-form equivalent of an EFG in linear time per iteration in the game tree size using a kernel trick. The resulting algorithm, Kernelized OMWU (KOMWU), applies more broadly to all convex games whose strategy space is a polytope with 0/1 integral vertices, as long as the kernel can be evaluated efficiently. In the particular case of EFGs, KOMWU closes several standing gaps between NFG and EFG learning, by enabling direct, black-box transfer to EFGs of desirable properties of learning dynamics that were so far known to be achievable only in NFGs. Specifically, KOMWU gives the first algorithm that guarantees at the same time last-iterate convergence, lower dependence on the size of the game tree than all prior algorithms, and $\tilde{\mathcal{O}}(1)$ regret when followed by all players.

Policy Optimization in Adversarial MDPs: Improved Exploration via Dilated Bonuses

Policy optimization is a widely-used method in reinforcement learning. Due to its local-search nature, however, theoretical guarantees on global optimality often rely on extra assumptions on the Markov Decision Processes (MDPs) that bypass the challenge of global exploration. To eliminate the need of such assumptions, in this work, we develop a general solution that adds dilated bonuses to the policy update to facilitate global exploration. To showcase the power and generality of this technique, we apply it to several episodic MDP settings with adversarial losses and bandit feedback, improving and generalizing the state-of-the-art. Specifically, in the tabular case, we obtain $\widetilde{\mathcal{O}}(\sqrt{T})$ regret where $T$ is the number of episodes, improving the $\widetilde{\mathcal{O}}({T}^{2/3})$ regret bound by Shani et al. (2020). When the number of states is infinite, under the assumption that the state-action values are linear in some low-dimensional features, we obtain $\widetilde{\mathcal{O}}({T}^{2/3})$ regret with the help of a simulator, matching the result of Neu and Olkhovskaya (2020) while importantly removing the need of an exploratory policy that their algorithm requires. When a simulator is unavailable, we further consider a linear MDP setting and obtain $\widetilde{\mathcal{O}}({T}^{14/15})$ regret, which is the first result for linear MDPs with adversarial losses and bandit feedback.

Last-iterate Convergence in Extensive-Form Games

Regret-based algorithms are highly efficient at finding approximate Nash equilibria in sequential games such as poker games. However, most regret-based algorithms, including counterfactual regret minimization (CFR) and its variants, rely on iterate averaging to achieve convergence. Inspired by recent advances on last-iterate convergence of optimistic algorithms in zero-sum normal-form games, we study this phenomenon in sequential games, and provide a comprehensive study of last-iterate convergence for zero-sum extensive-form games with perfect recall (EFGs), using various optimistic regret-minimization algorithms over treeplexes. This includes algorithms using the vanilla entropy or squared Euclidean norm regularizers, as well as their dilated versions which admit more efficient implementation. In contrast to CFR, we show that all of these algorithms enjoy last-iterate convergence, with some of them even converging exponentially fast. We also provide experiments to further support our theoretical results.