Optimal level set estimation for non-parametric tournament and crowdsourcing problems

Motivated by crowdsourcing, we consider a problem where we partially observe the correctness of the answers of $n$ experts on $d$ questions. In this paper, we assume that both the experts and the questions can be ordered, namely that the matrix $M$ containing the probability that expert $i$ answers correctly to question $j$ is bi-isotonic up to a permutation of it rows and columns. When $n=d$, this also encompasses the strongly stochastic transitive (SST) model from the tournament literature. Here, we focus on the relevant problem of deciphering small entries of $M$ from large entries of $M$, which is key in crowdsourcing for efficient allocation of workers to questions. More precisely, we aim at recovering a (or several) level set $p$ of the matrix up to a precision $h$, namely recovering resp. the sets of positions $(i,j)$ in $M$ such that $M_{ij}>p+h$ and $M_{i,j}<p-h$. We consider, as a loss measure, the number of misclassified entries. As our main result, we construct an efficient polynomial-time algorithm that turns out to be minimax optimal for this classification problem. This heavily contrasts with existing literature in the SST model where, for the stronger reconstruction loss, statistical-computational gaps have been conjectured. More generally, this shades light on the nature of statistical-computational gaps for permutations models.

A simple and improved algorithm for noisy, convex, zeroth-order optimisation

In this paper, we study the problem of noisy, convex, zeroth order optimisation of a function $f$ over a bounded convex set $\bar{\mathcal X}\subset \mathbb{R}^d$. Given a budget $n$ of noisy queries to the function $f$ that can be allocated sequentially and adaptively, our aim is to construct an algorithm that returns a point $\hat x\in \bar{\mathcal X}$ such that $f(\hat x)$ is as small as possible. We provide a conceptually simple method inspired by the textbook center of gravity method, but adapted to the noisy and zeroth order setting. We prove that this method is such that the $f(\hat x) - \min_{x\in \bar{\mathcal X}} f(x)$ is of smaller order than $d^2/\sqrt{n}$ up to poly-logarithmic terms. We slightly improve upon existing literature, where to the best of our knowledge the best known rate is in [Lattimore, 2024] is of order $d^{2.5}/\sqrt{n}$, albeit for a more challenging problem. Our main contribution is however conceptual, as we believe that our algorithm and its analysis bring novel ideas and are significantly simpler than existing approaches.

Active clustering with bandit feedback

We investigate the Active Clustering Problem (ACP). A learner interacts with an $N$-armed stochastic bandit with $d$-dimensional subGaussian feedback. There exists a hidden partition of the arms into $K$ groups, such that arms within the same group, share the same mean vector. The learner's task is to uncover this hidden partition with the smallest budget - i.e., the least number of observation - and with a probability of error smaller than a prescribed constant $\delta$. In this paper, (i) we derive a non-asymptotic lower bound for the budget, and (ii) we introduce the computationally efficient ACB algorithm, whose budget matches the lower bound in most regimes. We improve on the performance of a uniform sampling strategy. Importantly, contrary to the batch setting, we establish that there is no computation-information gap in the active setting.

Online Learning with Feedback Graphs: The True Shape of Regret

Sequential learning with feedback graphs is a natural extension of the multi-armed bandit problem where the problem is equipped with an underlying graph structure that provides additional information - playing an action reveals the losses of all the neighbors of the action. This problem was introduced by \citet{mannor2011} and received considerable attention in recent years. It is generally stated in the literature that the minimax regret rate for this problem is of order $\sqrt{\alpha T}$, where $\alpha$ is the independence number of the graph, and $T$ is the time horizon. However, this is proven only when the number of rounds $T$ is larger than $\alpha^3$, which poses a significant restriction for the usability of this result in large graphs. In this paper, we define a new quantity $R^*$, called the \emph{problem complexity}, and prove that the minimax regret is proportional to $R^*$ for any graph and time horizon $T$. Introducing an intricate exploration strategy, we define the \mainAlgorithm algorithm that achieves the minimax optimal regret bound and becomes the first provably optimal algorithm for this setting, even if $T$ is smaller than $\alpha^3$.

Active Ranking of Experts Based on their Performances in Many Tasks

We consider the problem of ranking n experts based on their performances on d tasks. We make a monotonicity assumption stating that for each pair of experts, one outperforms the other on all tasks. We consider the sequential setting where in each round, the learner has access to noisy evaluations of actively chosen pair of expert-task, given the information available up to the actual round. Given a confidence parameter $\delta$ $\in$ (0, 1), we provide strategies allowing to recover the correct ranking of experts and develop a bound on the total number of queries made by our algorithm that hold with probability at least 1 -- $\delta$. We show that our strategy is adaptive to the complexity of the problem (our bounds are instance dependent), and develop matching lower bounds up to a poly-logarithmic factor. Finally, we adapt our strategy to the relaxed problem of best expert identification and provide numerical simulation consistent with our theoretical results.

The price of unfairness in linear bandits with biased feedback

Artificial intelligence is increasingly used in a wide range of decision making scenarios with higher and higher stakes. At the same time, recent work has highlighted that these algorithms can be dangerously biased, and that their results often need to be corrected to avoid leading to unfair decisions. In this paper, we study the problem of sequential decision making with biased linear bandit feedback. At each round, a player selects an action described by a covariate and by a sensitive attribute. She receives a reward corresponding to the covariates of the action that she has chosen, but only observe a biased evaluation of this reward, where the bias depends on the sensitive attribute. To tackle this problem, we design a Fair Phased Elimination algorithm. We establish an upper bound on its worst-case regret, showing that it is smaller than C$\kappa$ 1/3 * log(T) 1/3 T 2/3 , where C is a numerical constant and $\kappa$ * an explicit geometrical constant characterizing the difficulty of bias estimation. The worst case regret is higher than the dT 1/2 log(T) regret rate obtained under unbiased feedback. We show that this rate cannot be improved for all instances : we obtain lower bounds on the worst-case regret for some sets of actions showing that this rate is tight up to a sub-logarithmic factor. We also obtain gap-dependent upper bounds on the regret, and establish matching lower bounds for some problem instance. Interestingly, the gap-dependent rates reveal the existence of non-trivial instances where the problem is no more difficult than its unbiased counterpart.

Problem Dependent View on Structured Thresholding Bandit Problems

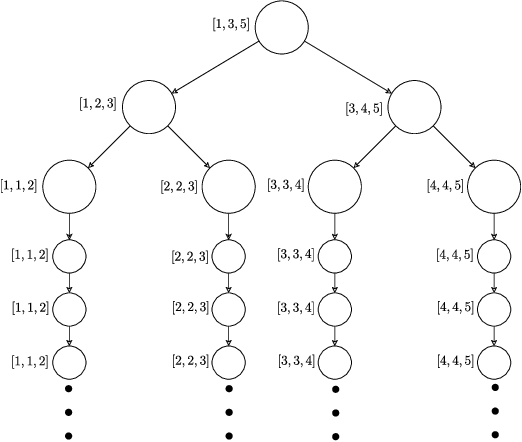
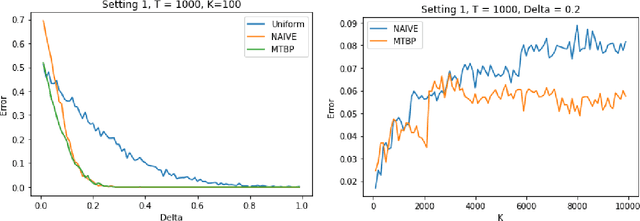
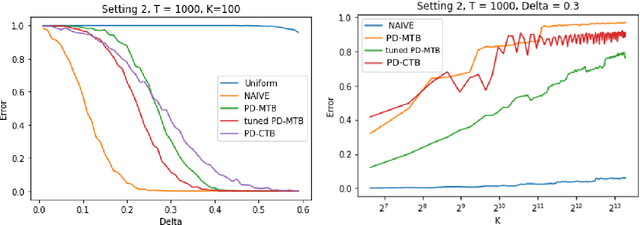
We investigate the problem dependent regime in the stochastic Thresholding Bandit problem (TBP) under several shape constraints. In the TBP, the objective of the learner is to output, at the end of a sequential game, the set of arms whose means are above a given threshold. The vanilla, unstructured, case is already well studied in the literature. Taking $K$ as the number of arms, we consider the case where (i) the sequence of arm's means $(\mu_k)_{k=1}^K$ is monotonically increasing (MTBP) and (ii) the case where $(\mu_k)_{k=1}^K$ is concave (CTBP). We consider both cases in the problem dependent regime and study the probability of error - i.e. the probability to mis-classify at least one arm. In the fixed budget setting, we provide upper and lower bounds for the probability of error in both the concave and monotone settings, as well as associated algorithms. In both settings the bounds match in the problem dependent regime up to universal constants in the exponential.

Bandits with many optimal arms

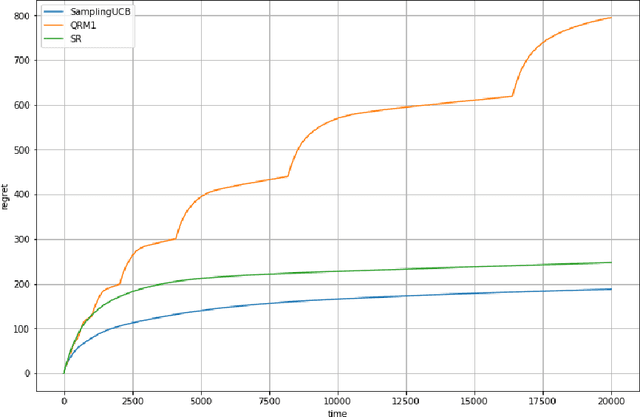
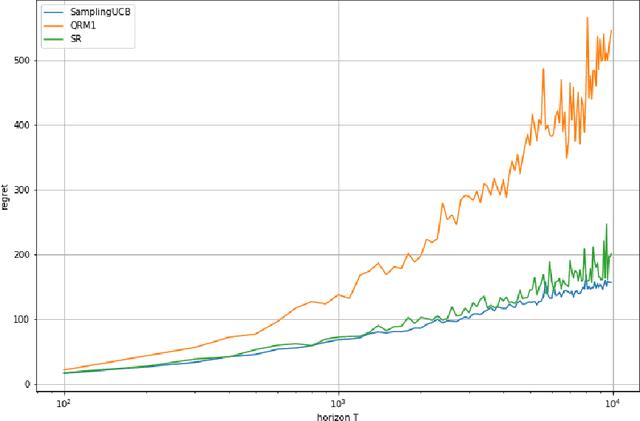
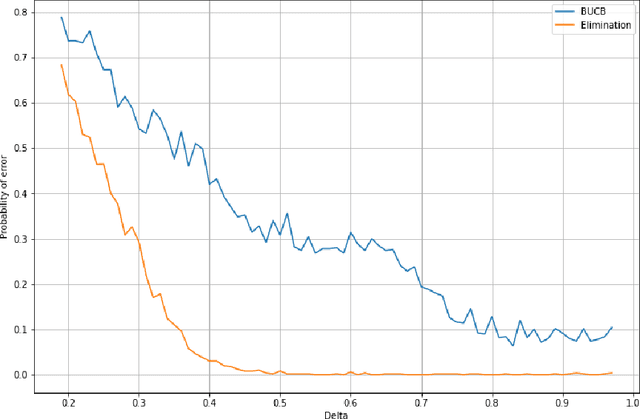
We consider a stochastic bandit problem with a possibly infinite number of arms. We write $p^*$ for the proportion of optimal arms and $\Delta$ for the minimal mean-gap between optimal and sub-optimal arms. We characterize the optimal learning rates both in the cumulative regret setting, and in the best-arm identification setting in terms of the problem parameters $T$ (the budget), $p^*$ and $\Delta$. For the objective of minimizing the cumulative regret, we provide a lower bound of order $\Omega(\log(T)/(p^*\Delta))$ and a UCB-style algorithm with matching upper bound up to a factor of $\log(1/\Delta)$. Our algorithm needs $p^*$ to calibrate its parameters, and we prove that this knowledge is necessary, since adapting to $p^*$ in this setting is impossible. For best-arm identification we also provide a lower bound of order $\Omega(\exp(-cT\Delta^2p^*))$ on the probability of outputting a sub-optimal arm where $c>0$ is an absolute constant. We also provide an elimination algorithm with an upper bound matching the lower bound up to a factor of order $\log(1/\Delta)$ in the exponential, and that does not need $p^*$ or $\Delta$ as parameter.

Generalized non-stationary bandits

In this paper, we study a non-stationary stochastic bandit problem, which generalizes the switching bandit problem. On top of the switching bandit problem (\textbf{Case a}), we are interested in three concrete examples: (\textbf{b}) the means of the arms are local polynomials, (\textbf{c}) the means of the arms are locally smooth, and (\textbf{d}) the gaps of the arms have a bounded number of inflexion points and where the highest arm mean cannot vary too much in a short range. These three settings are very different, but have in common the following: (i) the number of similarly-sized level sets of the logarithm of the gaps can be controlled, and (ii) the highest mean has a limited number of abrupt changes, and otherwise has limited variations. We propose a single algorithm in this general setting, that in particular solves in an efficient and unified way the four problems (a)-(d) mentioned.

The Elliptical Potential Lemma Revisited

This note proposes a new proof and new perspectives on the so-called Elliptical Potential Lemma. This result is important in online learning, especially for linear stochastic bandits. The original proof of the result, however short and elegant, does not give much flexibility on the type of potentials considered and we believe that this new interpretation can be of interest for future research in this field.