Stochastic Gradient Succeeds for Bandits

We show that the \emph{stochastic gradient} bandit algorithm converges to a \emph{globally optimal} policy at an $O(1/t)$ rate, even with a \emph{constant} step size. Remarkably, global convergence of the stochastic gradient bandit algorithm has not been previously established, even though it is an old algorithm known to be applicable to bandits. The new result is achieved by establishing two novel technical findings: first, the noise of the stochastic updates in the gradient bandit algorithm satisfies a strong ``growth condition'' property, where the variance diminishes whenever progress becomes small, implying that additional noise control via diminishing step sizes is unnecessary; second, a form of ``weak exploration'' is automatically achieved through the stochastic gradient updates, since they prevent the action probabilities from decaying faster than $O(1/t)$, thus ensuring that every action is sampled infinitely often with probability $1$. These two findings can be used to show that the stochastic gradient update is already ``sufficient'' for bandits in the sense that exploration versus exploitation is automatically balanced in a manner that ensures almost sure convergence to a global optimum. These novel theoretical findings are further verified by experimental results.

Sample Efficient Deep Reinforcement Learning via Local Planning

The focus of this work is sample-efficient deep reinforcement learning (RL) with a simulator. One useful property of simulators is that it is typically easy to reset the environment to a previously observed state. We propose an algorithmic framework, named uncertainty-first local planning (UFLP), that takes advantage of this property. Concretely, in each data collection iteration, with some probability, our meta-algorithm resets the environment to an observed state which has high uncertainty, instead of sampling according to the initial-state distribution. The agent-environment interaction then proceeds as in the standard online RL setting. We demonstrate that this simple procedure can dramatically improve the sample cost of several baseline RL algorithms on difficult exploration tasks. Notably, with our framework, we can achieve super-human performance on the notoriously hard Atari game, Montezuma's Revenge, with a simple (distributional) double DQN. Our work can be seen as an efficient approximate implementation of an existing algorithm with theoretical guarantees, which offers an interpretation of the positive empirical results.

The Role of Baselines in Policy Gradient Optimization

We study the effect of baselines in on-policy stochastic policy gradient optimization, and close the gap between the theory and practice of policy optimization methods. Our first contribution is to show that the \emph{state value} baseline allows on-policy stochastic \emph{natural} policy gradient (NPG) to converge to a globally optimal policy at an $O(1/t)$ rate, which was not previously known. The analysis relies on two novel findings: the expected progress of the NPG update satisfies a stochastic version of the non-uniform \L{}ojasiewicz (N\L{}) inequality, and with probability 1 the state value baseline prevents the optimal action's probability from vanishing, thus ensuring sufficient exploration. Importantly, these results provide a new understanding of the role of baselines in stochastic policy gradient: by showing that the variance of natural policy gradient estimates remains unbounded with or without a baseline, we find that variance reduction \emph{cannot} explain their utility in this setting. Instead, the analysis reveals that the primary effect of the value baseline is to \textbf{reduce the aggressiveness of the updates} rather than their variance. That is, we demonstrate that a finite variance is \emph{not necessary} for almost sure convergence of stochastic NPG, while controlling update aggressiveness is both necessary and sufficient. Additional experimental results verify these theoretical findings.

Optimistic MLE -- A Generic Model-based Algorithm for Partially Observable Sequential Decision Making

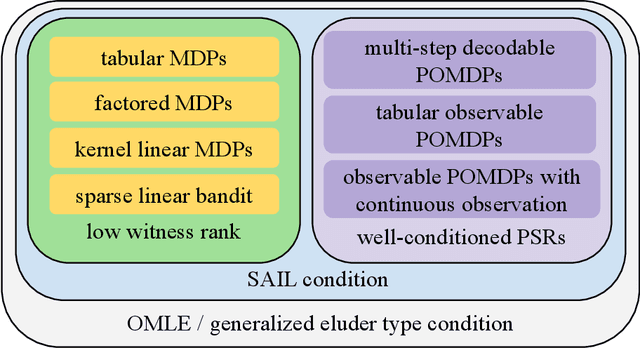
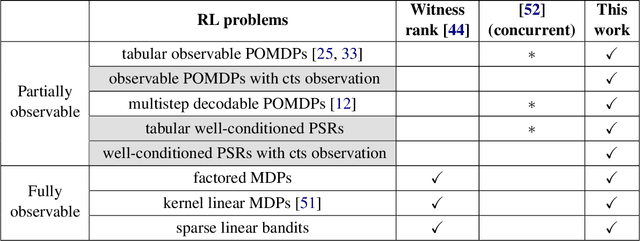
This paper introduces a simple efficient learning algorithms for general sequential decision making. The algorithm combines Optimism for exploration with Maximum Likelihood Estimation for model estimation, which is thus named OMLE. We prove that OMLE learns the near-optimal policies of an enormously rich class of sequential decision making problems in a polynomial number of samples. This rich class includes not only a majority of known tractable model-based Reinforcement Learning (RL) problems (such as tabular MDPs, factored MDPs, low witness rank problems, tabular weakly-revealing/observable POMDPs and multi-step decodable POMDPs), but also many new challenging RL problems especially in the partially observable setting that were not previously known to be tractable. Notably, the new problems addressed by this paper include (1) observable POMDPs with continuous observation and function approximation, where we achieve the first sample complexity that is completely independent of the size of observation space; (2) well-conditioned low-rank sequential decision making problems (also known as Predictive State Representations (PSRs)), which include and generalize all known tractable POMDP examples under a more intrinsic representation; (3) general sequential decision making problems under SAIL condition, which unifies our existing understandings of model-based RL in both fully observable and partially observable settings. SAIL condition is identified by this paper, which can be viewed as a natural generalization of Bellman/witness rank to address partial observability.

Towards Painless Policy Optimization for Constrained MDPs

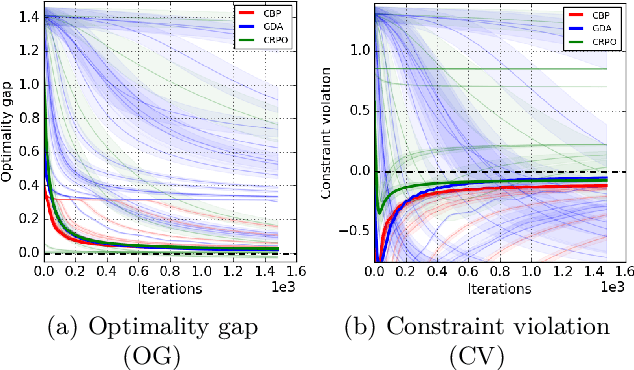
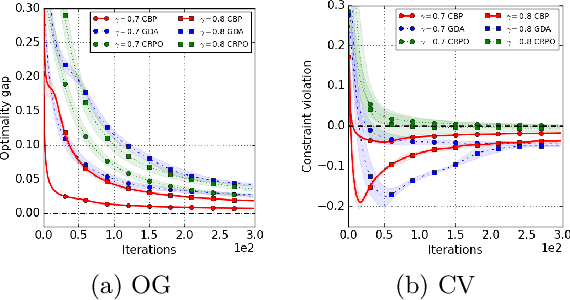
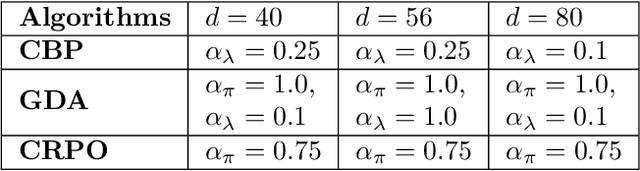
We study policy optimization in an infinite horizon, $\gamma$-discounted constrained Markov decision process (CMDP). Our objective is to return a policy that achieves large expected reward with a small constraint violation. We consider the online setting with linear function approximation and assume global access to the corresponding features. We propose a generic primal-dual framework that allows us to bound the reward sub-optimality and constraint violation for arbitrary algorithms in terms of their primal and dual regret on online linear optimization problems. We instantiate this framework to use coin-betting algorithms and propose the Coin Betting Politex (CBP) algorithm. Assuming that the action-value functions are $\varepsilon_b$-close to the span of the $d$-dimensional state-action features and no sampling errors, we prove that $T$ iterations of CBP result in an $O\left(\frac{1}{(1 - \gamma)^3 \sqrt{T}} + \frac{\varepsilon_b\sqrt{d}}{(1 - \gamma)^2} \right)$ reward sub-optimality and an $O\left(\frac{1}{(1 - \gamma)^2 \sqrt{T}} + \frac{\varepsilon_b \sqrt{d}}{1 - \gamma} \right)$ constraint violation. Importantly, unlike gradient descent-ascent and other recent methods, CBP does not require extensive hyperparameter tuning. Via experiments on synthetic and Cartpole environments, we demonstrate the effectiveness and robustness of CBP.

Understanding the Effect of Stochasticity in Policy Optimization

We study the effect of stochasticity in on-policy policy optimization, and make the following four contributions. First, we show that the preferability of optimization methods depends critically on whether stochastic versus exact gradients are used. In particular, unlike the true gradient setting, geometric information cannot be easily exploited in the stochastic case for accelerating policy optimization without detrimental consequences or impractical assumptions. Second, to explain these findings we introduce the concept of committal rate for stochastic policy optimization, and show that this can serve as a criterion for determining almost sure convergence to global optimality. Third, we show that in the absence of external oracle information, which allows an algorithm to determine the difference between optimal and sub-optimal actions given only on-policy samples, there is an inherent trade-off between exploiting geometry to accelerate convergence versus achieving optimality almost surely. That is, an uninformed algorithm either converges to a globally optimal policy with probability $1$ but at a rate no better than $O(1/t)$, or it achieves faster than $O(1/t)$ convergence but then must fail to converge to the globally optimal policy with some positive probability. Finally, we use the committal rate theory to explain why practical policy optimization methods are sensitive to random initialization, then develop an ensemble method that can be guaranteed to achieve near-optimal solutions with high probability.

On the Sample Complexity of Batch Reinforcement Learning with Policy-Induced Data

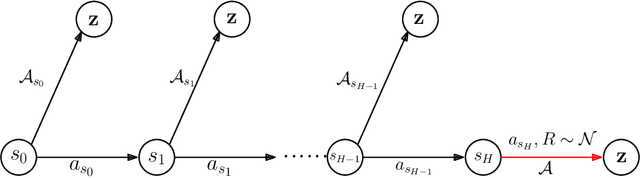
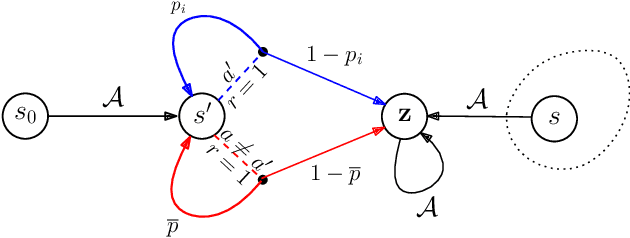
We study the fundamental question of the sample complexity of learning a good policy in finite Markov decision processes (MDPs) when the data available for learning is obtained by following a logging policy that must be chosen without knowledge of the underlying MDP. Our main results show that the sample complexity, the minimum number of transitions necessary and sufficient to obtain a good policy, is an exponential function of the relevant quantities when the planning horizon $H$ is finite. In particular, we prove that the sample complexity of obtaining $\epsilon$-optimal policies is at least $\Omega(\mathrm{A}^{\min(\mathrm{S}-1, H+1)})$ for $\gamma$-discounted problems, where $\mathrm{S}$ is the number of states, $\mathrm{A}$ is the number of actions, and $H$ is the effective horizon defined as $H=\lfloor \tfrac{\ln(1/\epsilon)}{\ln(1/\gamma)} \rfloor$; and it is at least $\Omega(\mathrm{A}^{\min(\mathrm{S}-1, H)}/\varepsilon^2)$ for finite horizon problems, where $H$ is the planning horizon of the problem. This lower bound is essentially matched by an upper bound. For the average-reward setting we show that there is no algorithm finding $\epsilon$-optimal policies with a finite amount of data.

On Multi-objective Policy Optimization as a Tool for Reinforcement Learning

Many advances that have improved the robustness and efficiency of deep reinforcement learning (RL) algorithms can, in one way or another, be understood as introducing additional objectives, or constraints, in the policy optimization step. This includes ideas as far ranging as exploration bonuses, entropy regularization, and regularization toward teachers or data priors when learning from experts or in offline RL. Often, task reward and auxiliary objectives are in conflict with each other and it is therefore natural to treat these examples as instances of multi-objective (MO) optimization problems. We study the principles underlying MORL and introduce a new algorithm, Distillation of a Mixture of Experts (DiME), that is intuitive and scale-invariant under some conditions. We highlight its strengths on standard MO benchmark problems and consider case studies in which we recast offline RL and learning from experts as MO problems. This leads to a natural algorithmic formulation that sheds light on the connection between existing approaches. For offline RL, we use the MO perspective to derive a simple algorithm, that optimizes for the standard RL objective plus a behavioral cloning term. This outperforms state-of-the-art on two established offline RL benchmarks.

Leveraging Non-uniformity in First-order Non-convex Optimization

Classical global convergence results for first-order methods rely on uniform smoothness and the \L{}ojasiewicz inequality. Motivated by properties of objective functions that arise in machine learning, we propose a non-uniform refinement of these notions, leading to \emph{Non-uniform Smoothness} (NS) and \emph{Non-uniform \L{}ojasiewicz inequality} (N\L{}). The new definitions inspire new geometry-aware first-order methods that are able to converge to global optimality faster than the classical $\Omega(1/t^2)$ lower bounds. To illustrate the power of these geometry-aware methods and their corresponding non-uniform analysis, we consider two important problems in machine learning: policy gradient optimization in reinforcement learning (PG), and generalized linear model training in supervised learning (GLM). For PG, we find that normalizing the gradient ascent method can accelerate convergence to $O(e^{-t})$ while incurring less overhead than existing algorithms. For GLM, we show that geometry-aware normalized gradient descent can also achieve a linear convergence rate, which significantly improves the best known results. We additionally show that the proposed geometry-aware descent methods escape landscape plateaus faster than standard gradient descent. Experimental results are used to illustrate and complement the theoretical findings.

On the Optimality of Batch Policy Optimization Algorithms

Batch policy optimization considers leveraging existing data for policy construction before interacting with an environment. Although interest in this problem has grown significantly in recent years, its theoretical foundations remain under-developed. To advance the understanding of this problem, we provide three results that characterize the limits and possibilities of batch policy optimization in the finite-armed stochastic bandit setting. First, we introduce a class of confidence-adjusted index algorithms that unifies optimistic and pessimistic principles in a common framework, which enables a general analysis. For this family, we show that any confidence-adjusted index algorithm is minimax optimal, whether it be optimistic, pessimistic or neutral. Our analysis reveals that instance-dependent optimality, commonly used to establish optimality of on-line stochastic bandit algorithms, cannot be achieved by any algorithm in the batch setting. In particular, for any algorithm that performs optimally in some environment, there exists another environment where the same algorithm suffers arbitrarily larger regret. Therefore, to establish a framework for distinguishing algorithms, we introduce a new weighted-minimax criterion that considers the inherent difficulty of optimal value prediction. We demonstrate how this criterion can be used to justify commonly used pessimistic principles for batch policy optimization.