Multi-Agent Stage-wise Conservative Linear Bandits

In many real-world applications such as recommendation systems, multiple learning agents must balance exploration and exploitation while maintaining safety guarantees to avoid catastrophic failures. We study the stochastic linear bandit problem in a multi-agent networked setting where agents must satisfy stage-wise conservative constraints. A network of $N$ agents collaboratively maximizes cumulative reward while ensuring that the expected reward at every round is no less than $(1-\alpha)$ times that of a baseline policy. Each agent observes local rewards with unknown parameters, but the network optimizes for the global parameter (average of local parameters). Agents communicate only with immediate neighbors, and each communication round incurs additional regret. We propose MA-SCLUCB (Multi-Agent Stage-wise Conservative Linear UCB), an episodic algorithm alternating between action selection and consensus-building phases. We prove that MA-SCLUCB achieves regret $\tilde{O}\left(\frac{d}{\sqrt{N}}\sqrt{T}\cdot\frac{\log(NT)}{\sqrt{\log(1/|\lambda_2|)}}\right)$ with high probability, where $d$ is the dimension, $T$ is the horizon, and $|\lambda_2|$ is the network's second largest eigenvalue magnitude. Our analysis shows: (i) collaboration yields $\frac{1}{\sqrt{N}}$ improvement despite local communication, (ii) communication overhead grows only logarithmically for well-connected networks, and (iii) stage-wise safety adds only lower-order regret. Thus, distributed learning with safety guarantees achieves near-optimal performance in reasonably connected networks.

Transport Based Mean Flows for Generative Modeling

Flow-matching generative models have emerged as a powerful paradigm for continuous data generation, achieving state-of-the-art results across domains such as images, 3D shapes, and point clouds. Despite their success, these models suffer from slow inference due to the requirement of numerous sequential sampling steps. Recent work has sought to accelerate inference by reducing the number of sampling steps. In particular, Mean Flows offer a one-step generation approach that delivers substantial speedups while retaining strong generative performance. Yet, in many continuous domains, Mean Flows fail to faithfully approximate the behavior of the original multi-step flow-matching process. In this work, we address this limitation by incorporating optimal transport-based sampling strategies into the Mean Flow framework, enabling one-step generators that better preserve the fidelity and diversity of the original multi-step flow process. Experiments on controlled low-dimensional settings and on high-dimensional tasks such as image generation, image-to-image translation, and point cloud generation demonstrate that our approach achieves superior inference accuracy in one-step generative modeling.

IN-RIL: Interleaved Reinforcement and Imitation Learning for Policy Fine-Tuning

Imitation learning (IL) and reinforcement learning (RL) each offer distinct advantages for robotics policy learning: IL provides stable learning from demonstrations, and RL promotes generalization through exploration. While existing robot learning approaches using IL-based pre-training followed by RL-based fine-tuning are promising, this two-step learning paradigm often suffers from instability and poor sample efficiency during the RL fine-tuning phase. In this work, we introduce IN-RIL, INterleaved Reinforcement learning and Imitation Learning, for policy fine-tuning, which periodically injects IL updates after multiple RL updates and hence can benefit from the stability of IL and the guidance of expert data for more efficient exploration throughout the entire fine-tuning process. Since IL and RL involve different optimization objectives, we develop gradient separation mechanisms to prevent destructive interference during \ABBR fine-tuning, by separating possibly conflicting gradient updates in orthogonal subspaces. Furthermore, we conduct rigorous analysis, and our findings shed light on why interleaving IL with RL stabilizes learning and improves sample-efficiency. Extensive experiments on 14 robot manipulation and locomotion tasks across 3 benchmarks, including FurnitureBench, OpenAI Gym, and Robomimic, demonstrate that \ABBR can significantly improve sample efficiency and mitigate performance collapse during online finetuning in both long- and short-horizon tasks with either sparse or dense rewards. IN-RIL, as a general plug-in compatible with various state-of-the-art RL algorithms, can significantly improve RL fine-tuning, e.g., from 12\% to 88\% with 6.3x improvement in the success rate on Robomimic Transport. Project page: https://github.com/ucd-dare/IN-RIL.

NuPlanQA: A Large-Scale Dataset and Benchmark for Multi-View Driving Scene Understanding in Multi-Modal Large Language Models

Recent advances in multi-modal large language models (MLLMs) have demonstrated strong performance across various domains; however, their ability to comprehend driving scenes remains less proven. The complexity of driving scenarios, which includes multi-view information, poses significant challenges for existing MLLMs. In this paper, we introduce NuPlanQA-Eval, a multi-view, multi-modal evaluation benchmark for driving scene understanding. To further support generalization to multi-view driving scenarios, we also propose NuPlanQA-1M, a large-scale dataset comprising 1M real-world visual question-answering (VQA) pairs. For context-aware analysis of traffic scenes, we categorize our dataset into nine subtasks across three core skills: Road Environment Perception, Spatial Relations Recognition, and Ego-Centric Reasoning. Furthermore, we present BEV-LLM, integrating Bird's-Eye-View (BEV) features from multi-view images into MLLMs. Our evaluation results reveal key challenges that existing MLLMs face in driving scene-specific perception and spatial reasoning from ego-centric perspectives. In contrast, BEV-LLM demonstrates remarkable adaptability to this domain, outperforming other models in six of the nine subtasks. These findings highlight how BEV integration enhances multi-view MLLMs while also identifying key areas that require further refinement for effective adaptation to driving scenes. To facilitate further research, we publicly release NuPlanQA at https://github.com/sungyeonparkk/NuPlanQA.

Cooperative Multi-Agent Constrained Stochastic Linear Bandits

In this study, we explore a collaborative multi-agent stochastic linear bandit setting involving a network of $N$ agents that communicate locally to minimize their collective regret while keeping their expected cost under a specified threshold $\tau$. Each agent encounters a distinct linear bandit problem characterized by its own reward and cost parameters, i.e., local parameters. The goal of the agents is to determine the best overall action corresponding to the average of these parameters, or so-called global parameters. In each round, an agent is randomly chosen to select an action based on its current knowledge of the system. This chosen action is then executed by all agents, then they observe their individual rewards and costs. We propose a safe distributed upper confidence bound algorithm, so called \textit{MA-OPLB}, and establish a high probability bound on its $T$-round regret. MA-OPLB utilizes an accelerated consensus method, where agents can compute an estimate of the average rewards and costs across the network by communicating the proper information with their neighbors. We show that our regret bound is of order $ \mathcal{O}\left(\frac{d}{\tau-c_0}\frac{\log(NT)^2}{\sqrt{N}}\sqrt{\frac{T}{\log(1/|\lambda_2|)}}\right)$, where $\lambda_2$ is the second largest (in absolute value) eigenvalue of the communication matrix, and $\tau-c_0$ is the known cost gap of a feasible action. We also experimentally show the performance of our proposed algorithm in different network structures.

Convex Methods for Constrained Linear Bandits

Recently, bandit optimization has received significant attention in real-world safety-critical systems that involve repeated interactions with humans. While there exist various algorithms with performance guarantees in the literature, practical implementation of the algorithms has not received as much attention. This work presents a comprehensive study on the computational aspects of safe bandit algorithms, specifically safe linear bandits, by introducing a framework that leverages convex programming tools to create computationally efficient policies. In particular, we first characterize the properties of the optimal policy for safe linear bandit problem and then propose an end-to-end pipeline of safe linear bandit algorithms that only involves solving convex problems. We also numerically evaluate the performance of our proposed methods.

Improved Bayesian Regret Bounds for Thompson Sampling in Reinforcement Learning

In this paper, we prove the first Bayesian regret bounds for Thompson Sampling in reinforcement learning in a multitude of settings. We simplify the learning problem using a discrete set of surrogate environments, and present a refined analysis of the information ratio using posterior consistency. This leads to an upper bound of order $\widetilde{O}(H\sqrt{d_{l_1}T})$ in the time inhomogeneous reinforcement learning problem where $H$ is the episode length and $d_{l_1}$ is the Kolmogorov $l_1-$dimension of the space of environments. We then find concrete bounds of $d_{l_1}$ in a variety of settings, such as tabular, linear and finite mixtures, and discuss how how our results are either the first of their kind or improve the state-of-the-art.

Controlling the Latent Space of GANs through Reinforcement Learning: A Case Study on Task-based Image-to-Image Translation

Generative Adversarial Networks (GAN) have emerged as a formidable AI tool to generate realistic outputs based on training datasets. However, the challenge of exerting control over the generation process of GANs remains a significant hurdle. In this paper, we propose a novel methodology to address this issue by integrating a reinforcement learning (RL) agent with a latent-space GAN (l-GAN), thereby facilitating the generation of desired outputs. More specifically, we have developed an actor-critic RL agent with a meticulously designed reward policy, enabling it to acquire proficiency in navigating the latent space of the l-GAN and generating outputs based on specified tasks. To substantiate the efficacy of our approach, we have conducted a series of experiments employing the MNIST dataset, including arithmetic addition as an illustrative task. The outcomes of these experiments serve to validate our methodology. Our pioneering integration of an RL agent with a GAN model represents a novel advancement, holding great potential for enhancing generative networks in the future.

Predicting Parameters for Modeling Traffic Participants

Accurately modeling the behavior of traffic participants is essential for safely and efficiently navigating an autonomous vehicle through heavy traffic. We propose a method, based on the intelligent driver model, that allows us to accurately model individual driver behaviors from only a small number of frames using easily observable features. On average, this method makes prediction errors that have less than 1 meter difference from an oracle with full-information when analyzed over a 10-second horizon of highway driving. We then validate the efficiency of our method through extensive analysis against a competitive data-driven method such as Reinforcement Learning that may be of independent interest.

Collaborative Multi-agent Stochastic Linear Bandits

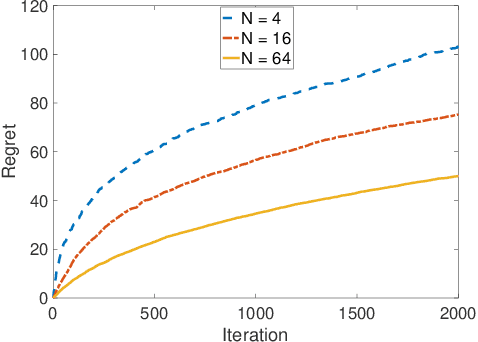
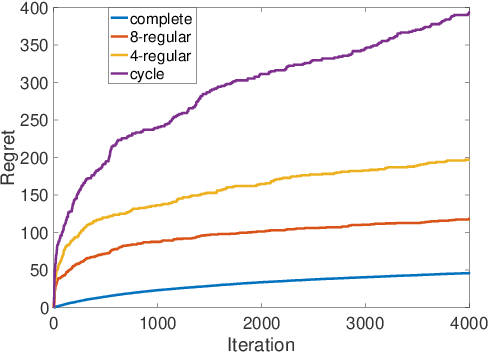
We study a collaborative multi-agent stochastic linear bandit setting, where $N$ agents that form a network communicate locally to minimize their overall regret. In this setting, each agent has its own linear bandit problem (its own reward parameter) and the goal is to select the best global action w.r.t. the average of their reward parameters. At each round, each agent proposes an action, and one action is randomly selected and played as the network action. All the agents observe the corresponding rewards of the played actions and use an accelerated consensus procedure to compute an estimate of the average of the rewards obtained by all the agents. We propose a distributed upper confidence bound (UCB) algorithm and prove a high probability bound on its $T$-round regret in which we include a linear growth of regret associated with each communication round. Our regret bound is of order $\mathcal{O}\Big(\sqrt{\frac{T}{N \log(1/|\lambda_2|)}}\cdot (\log T)^2\Big)$, where $\lambda_2$ is the second largest (in absolute value) eigenvalue of the communication matrix.