Improving White-box Robustness of Pre-processing Defenses via Joint Adversarial Training

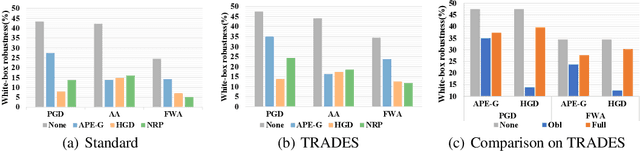
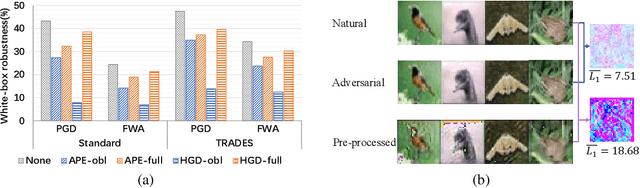
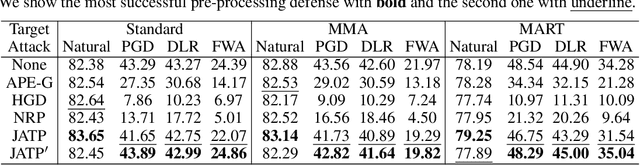
Deep neural networks (DNNs) are vulnerable to adversarial noise. A range of adversarial defense techniques have been proposed to mitigate the interference of adversarial noise, among which the input pre-processing methods are scalable and show great potential to safeguard DNNs. However, pre-processing methods may suffer from the robustness degradation effect, in which the defense reduces rather than improving the adversarial robustness of a target model in a white-box setting. A potential cause of this negative effect is that adversarial training examples are static and independent to the pre-processing model. To solve this problem, we investigate the influence of full adversarial examples which are crafted against the full model, and find they indeed have a positive impact on the robustness of defenses. Furthermore, we find that simply changing the adversarial training examples in pre-processing methods does not completely alleviate the robustness degradation effect. This is due to the adversarial risk of the pre-processed model being neglected, which is another cause of the robustness degradation effect. Motivated by above analyses, we propose a method called Joint Adversarial Training based Pre-processing (JATP) defense. Specifically, we formulate a feature similarity based adversarial risk for the pre-processing model by using full adversarial examples found in a feature space. Unlike standard adversarial training, we only update the pre-processing model, which prompts us to introduce a pixel-wise loss to improve its cross-model transferability. We then conduct a joint adversarial training on the pre-processing model to minimize this overall risk. Empirical results show that our method could effectively mitigate the robustness degradation effect across different target models in comparison to previous state-of-the-art approaches.

Bandwidth-based Step-Sizes for Non-Convex Stochastic Optimization

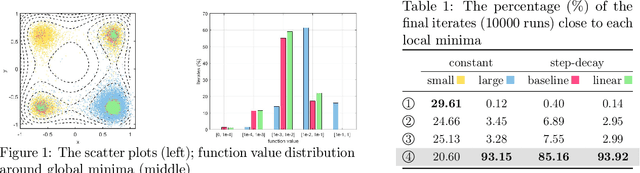
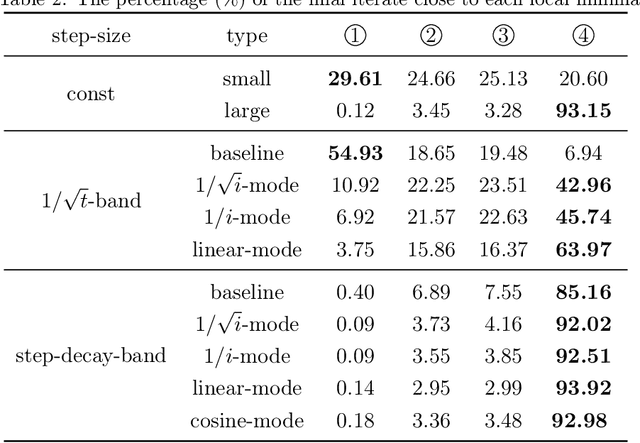
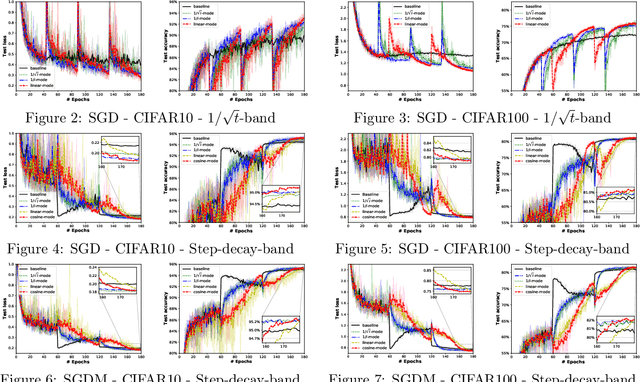
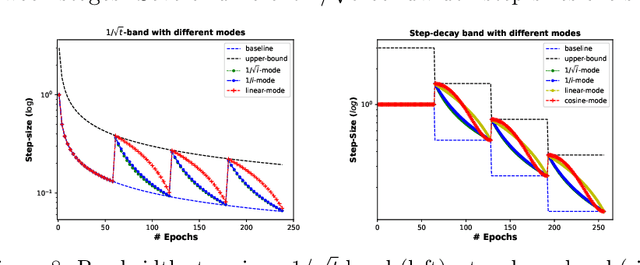
Many popular learning-rate schedules for deep neural networks combine a decaying trend with local perturbations that attempt to escape saddle points and bad local minima. We derive convergence guarantees for bandwidth-based step-sizes, a general class of learning-rates that are allowed to vary in a banded region. This framework includes cyclic and non-monotonic step-sizes for which no theoretical guarantees were previously known. We provide worst-case guarantees for SGD on smooth non-convex problems under several bandwidth-based step sizes, including stagewise $1/\sqrt{t}$ and the popular step-decay (constant and then drop by a constant), which is also shown to be optimal. Moreover, we show that its momentum variant (SGDM) converges as fast as SGD with the bandwidth-based step-decay step-size. Finally, we propose some novel step-size schemes in the bandwidth-based family and verify their efficiency on several deep neural network training tasks.

Removing Adversarial Noise in Class Activation Feature Space

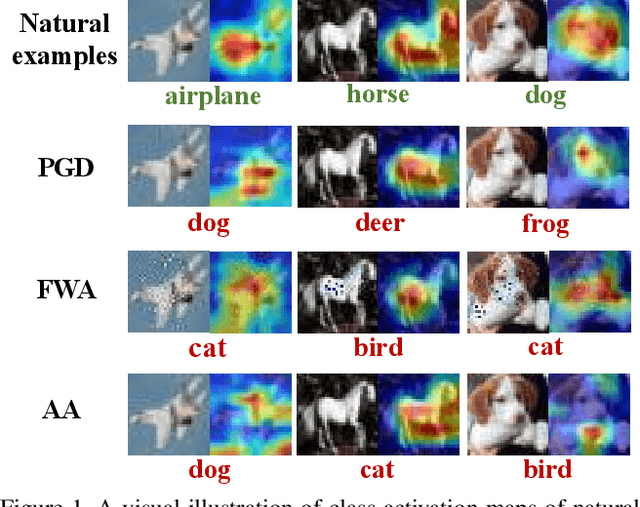
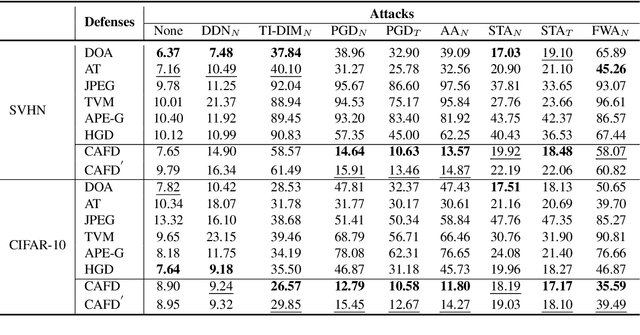
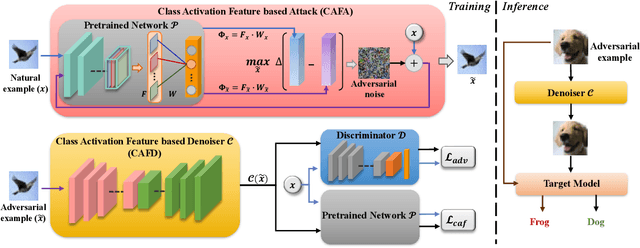
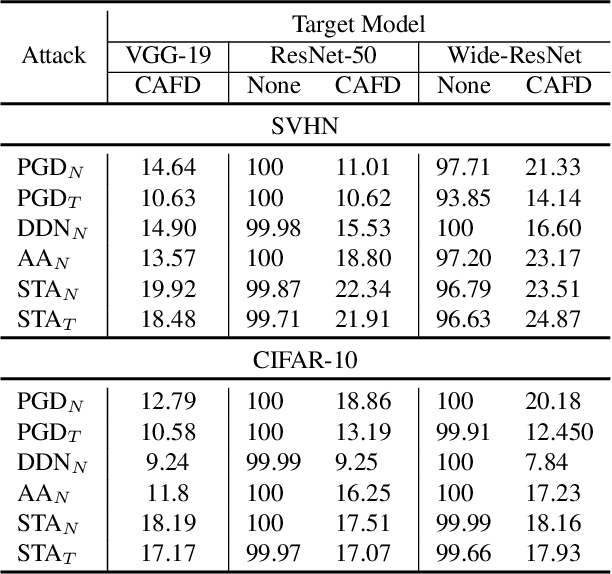
Deep neural networks (DNNs) are vulnerable to adversarial noise. Preprocessing based defenses could largely remove adversarial noise by processing inputs. However, they are typically affected by the error amplification effect, especially in the front of continuously evolving attacks. To solve this problem, in this paper, we propose to remove adversarial noise by implementing a self-supervised adversarial training mechanism in a class activation feature space. To be specific, we first maximize the disruptions to class activation features of natural examples to craft adversarial examples. Then, we train a denoising model to minimize the distances between the adversarial examples and the natural examples in the class activation feature space. Empirical evaluations demonstrate that our method could significantly enhance adversarial robustness in comparison to previous state-of-the-art approaches, especially against unseen adversarial attacks and adaptive attacks.

On the Convergence of Step Decay Step-Size for Stochastic Optimization

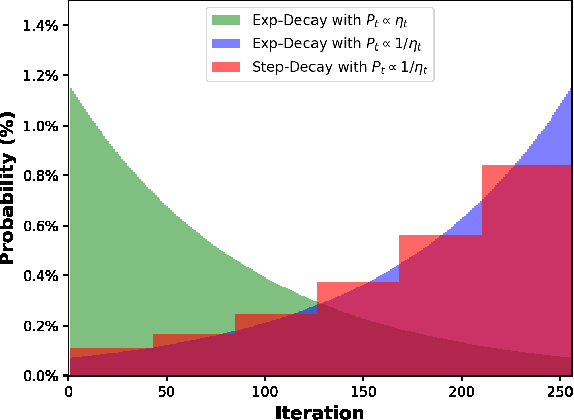
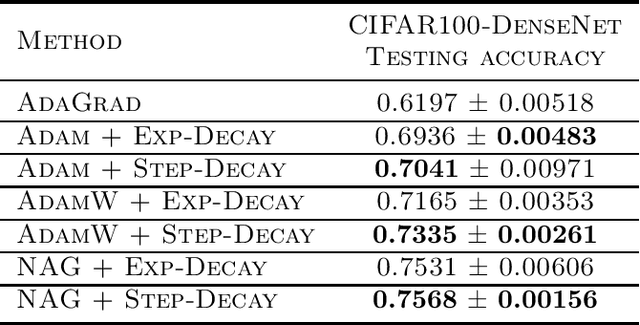
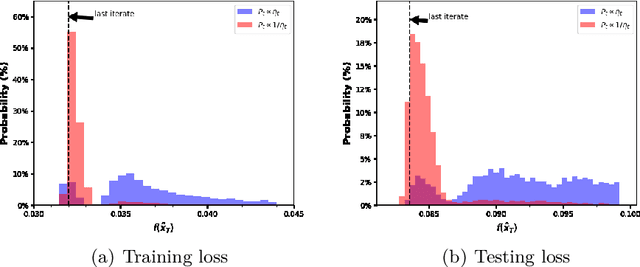
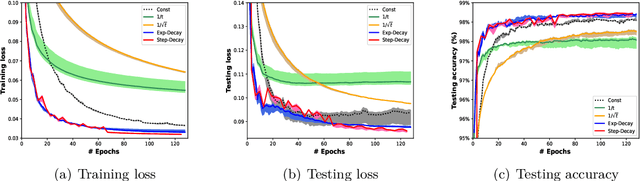
The convergence of stochastic gradient descent is highly dependent on the step-size, especially on non-convex problems such as neural network training. Step decay step-size schedules (constant and then cut) are widely used in practice because of their excellent convergence and generalization qualities, but their theoretical properties are not yet well understood. We provide the convergence results for step decay in the non-convex regime, ensuring that the gradient norm vanishes at an $\mathcal{O}(\ln T/\sqrt{T})$ rate. We also provide the convergence guarantees for general (possibly non-smooth) convex problems, ensuring an $\mathcal{O}(\ln T/\sqrt{T})$ convergence rate. Finally, in the strongly convex case, we establish an $\mathcal{O}(\ln T/T)$ rate for smooth problems, which we also prove to be tight, and an $\mathcal{O}(\ln^2 T /T)$ rate without the smoothness assumption. We illustrate the practical efficiency of the step decay step-size in several large scale deep neural network training tasks.

Asymmetric Heavy Tails and Implicit Bias in Gaussian Noise Injections

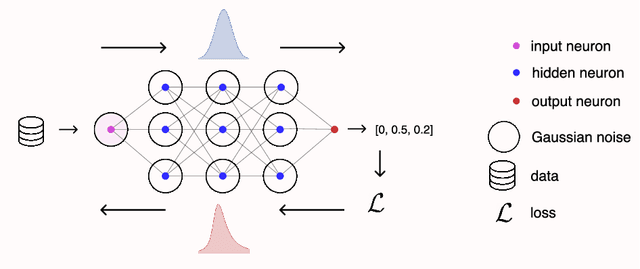
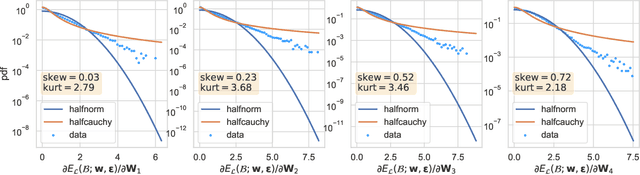
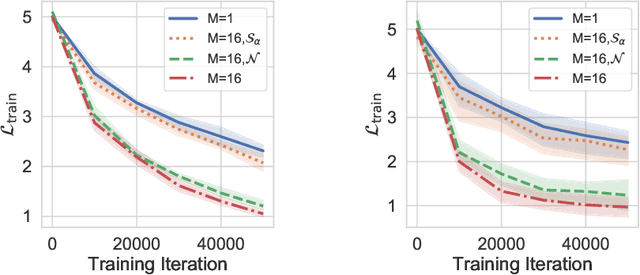
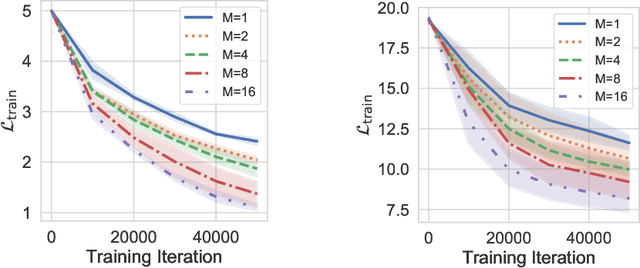
Gaussian noise injections (GNIs) are a family of simple and widely-used regularisation methods for training neural networks, where one injects additive or multiplicative Gaussian noise to the network activations at every iteration of the optimisation algorithm, which is typically chosen as stochastic gradient descent (SGD). In this paper we focus on the so-called `implicit effect' of GNIs, which is the effect of the injected noise on the dynamics of SGD. We show that this effect induces an asymmetric heavy-tailed noise on SGD gradient updates. In order to model this modified dynamics, we first develop a Langevin-like stochastic differential equation that is driven by a general family of asymmetric heavy-tailed noise. Using this model we then formally prove that GNIs induce an `implicit bias', which varies depending on the heaviness of the tails and the level of asymmetry. Our empirical results confirm that different types of neural networks trained with GNIs are well-modelled by the proposed dynamics and that the implicit effect of these injections induces a bias that degrades the performance of networks.

Generalised Perceptron Learning

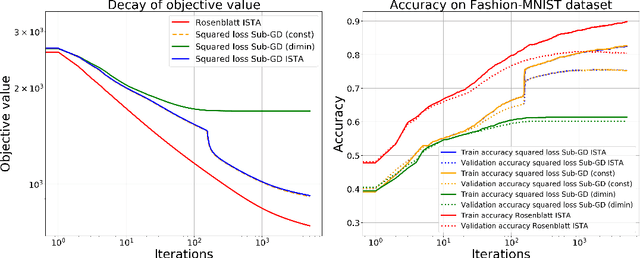
We present a generalisation of Rosenblatt's traditional perceptron learning algorithm to the class of proximal activation functions and demonstrate how this generalisation can be interpreted as an incremental gradient method applied to a novel energy function. This novel energy function is based on a generalised Bregman distance, for which the gradient with respect to the weights and biases does not require the differentiation of the activation function. The interpretation as an energy minimisation algorithm paves the way for many new algorithms, of which we explore a novel variant of the iterative soft-thresholding algorithm for the learning of sparse perceptrons.

Weakly Supervised Temporal Action Localization with Segment-Level Labels

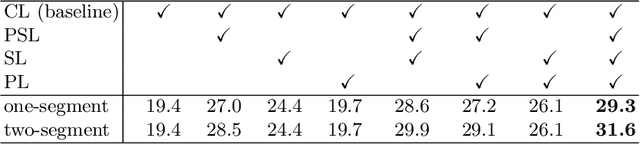
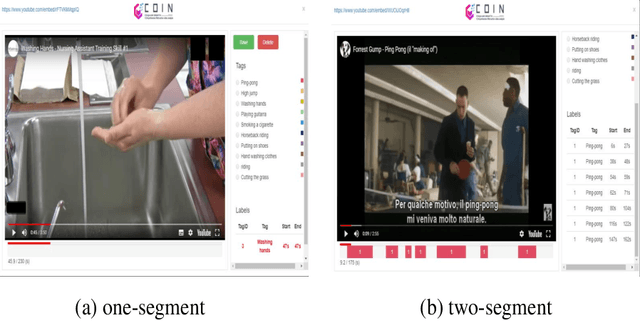
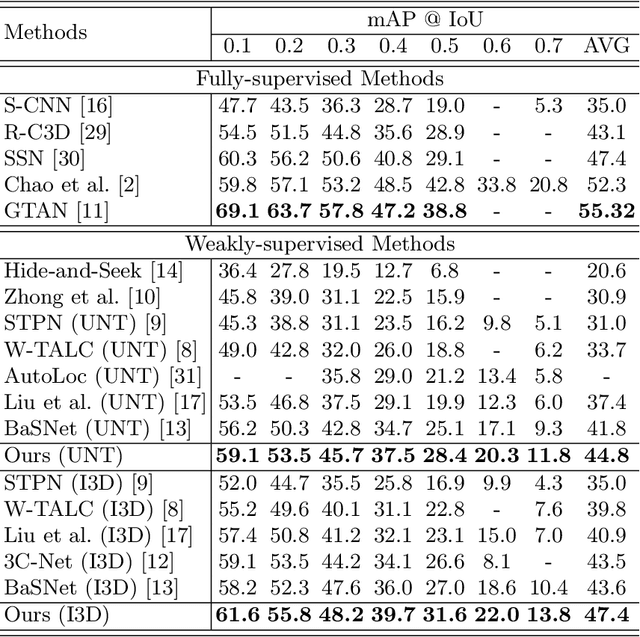
Temporal action localization presents a trade-off between test performance and annotation-time cost. Fully supervised methods achieve good performance with time-consuming boundary annotations. Weakly supervised methods with cheaper video-level category label annotations result in worse performance. In this paper, we introduce a new segment-level supervision setting: segments are labeled when annotators observe actions happening here. We incorporate this segment-level supervision along with a novel localization module in the training. Specifically, we devise a partial segment loss regarded as a loss sampling to learn integral action parts from labeled segments. Since the labeled segments are only parts of actions, the model tends to overfit along with the training process. To tackle this problem, we first obtain a similarity matrix from discriminative features guided by a sphere loss. Then, a propagation loss is devised based on the matrix to act as a regularization term, allowing implicit unlabeled segments propagation during training. Experiments validate that our method can outperform the video-level supervision methods with almost same the annotation time.

AIBench: An Industry Standard AI Benchmark Suite from Internet Services

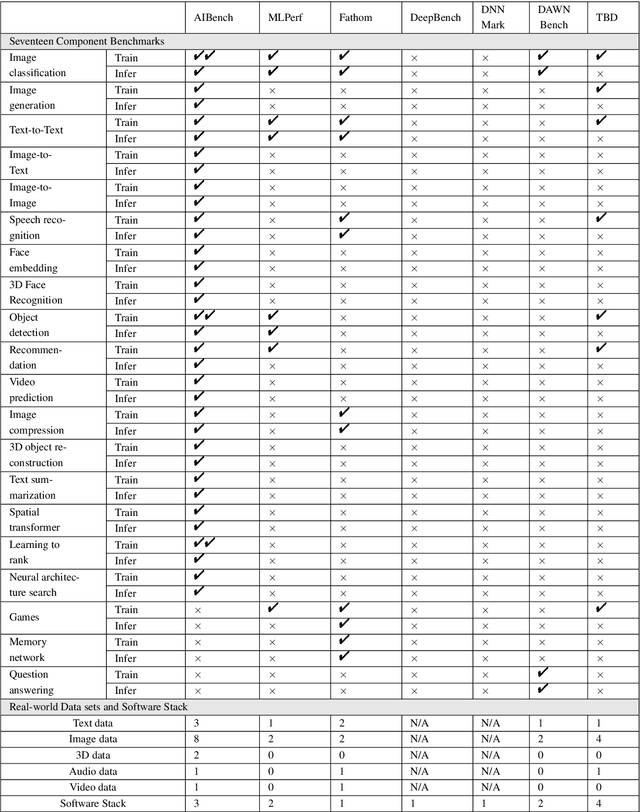
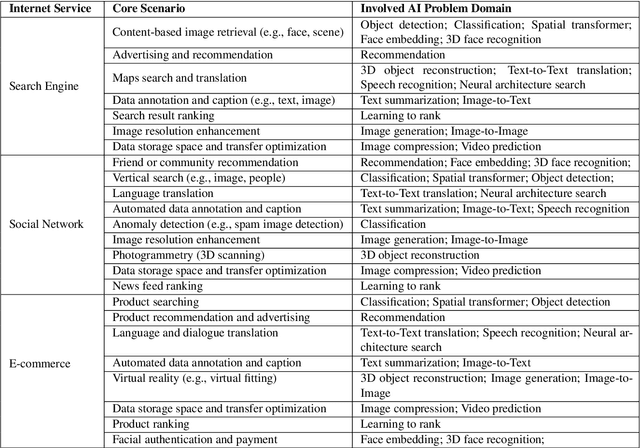
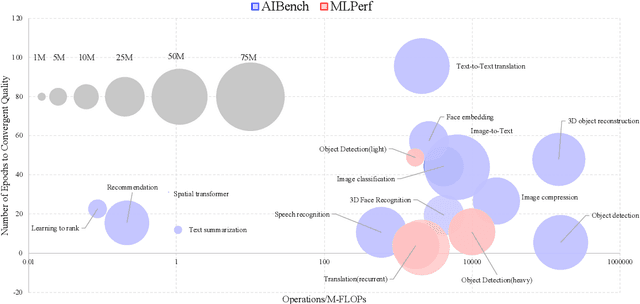
The booming successes of machine learning in different domains boost industry-scale deployments of innovative AI algorithms, systems, and architectures, and thus the importance of benchmarking grows. However, the confidential nature of the workloads, the paramount importance of the representativeness and diversity of benchmarks, and the prohibitive cost of training a state-of-the-art model mutually aggravate the AI benchmarking challenges. In this paper, we present a balanced AI benchmarking methodology for meeting the subtly different requirements of different stages in developing a new system/architecture and ranking/purchasing commercial off-the-shelf ones. Performing an exhaustive survey on the most important AI domain-Internet services with seventeen industry partners, we identify and include seventeen representative AI tasks to guarantee the representativeness and diversity of the benchmarks. Meanwhile, for reducing the benchmarking cost, we select a benchmark subset to a minimum-three tasks-according to the criteria: diversity of model complexity, computational cost, and convergence rate, repeatability, and having widely-accepted metrics or not. We contribute by far the most comprehensive AI benchmark suite-AIBench. The evaluations show AIBench outperforms MLPerf in terms of the diversity and representativeness of model complexity, computational cost, convergent rate, computation and memory access patterns, and hotspot functions. With respect to the AIBench full benchmarks, its subset shortens the benchmarking cost by 41%, while maintaining the primary workload characteristics. The specifications, source code, and performance numbers are publicly available from the web site http://www.benchcouncil.org/AIBench/index.html.

Robust Partial Matching for Person Search in the Wild

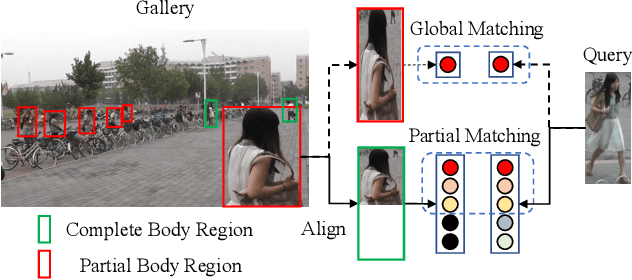
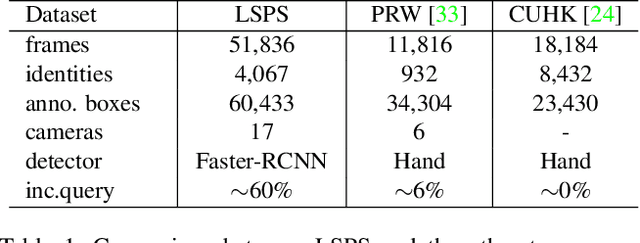
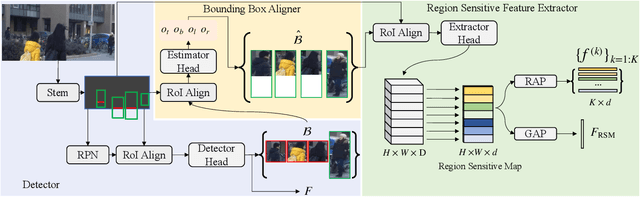
Various factors like occlusions, backgrounds, etc., would lead to misaligned detected bounding boxes , e.g., ones covering only portions of human body. This issue is common but overlooked by previous person search works. To alleviate this issue, this paper proposes an Align-to-Part Network (APNet) for person detection and re-Identification (reID). APNet refines detected bounding boxes to cover the estimated holistic body regions, from which discriminative part features can be extracted and aligned. Aligned part features naturally formulate reID as a partial feature matching procedure, where valid part features are selected for similarity computation, while part features on occluded or noisy regions are discarded. This design enhances the robustness of person search to real-world challenges with marginal computation overhead. This paper also contributes a Large-Scale dataset for Person Search in the wild (LSPS), which is by far the largest and the most challenging dataset for person search. Experiments show that APNet brings considerable performance improvement on LSPS. Meanwhile, it achieves competitive performance on existing person search benchmarks like CUHK-SYSU and PRW.

Non-Convex Stochastic Optimization via Non-Reversible Stochastic Gradient Langevin Dynamics

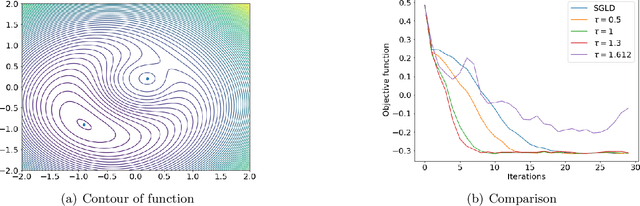
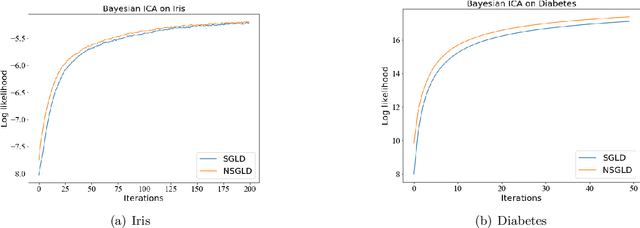
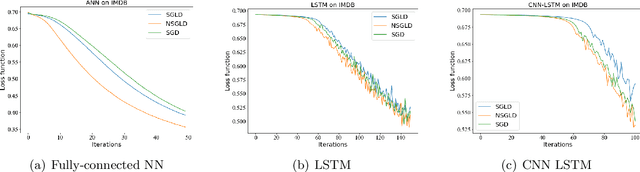
Stochastic gradient Langevin dynamics (SGLD) is a poweful algorithm for optimizing a non-convex objective, where a controlled and properly scaled Gaussian noise is added to the stochastic gradients to steer the iterates towards a global minimum. SGLD is based on the overdamped Langevin diffusion which is reversible in time. By adding an anti-symmetric matrix to the drift term of the overdamped Langevin diffusion, one gets a non-reversible diffusion that converges to the same stationary distribution with a faster convergence rate. In this paper, we study the non-reversible stochastic gradient Langevin dynamics (NSGLD) which is based on discretization of the non-reversible Langevin diffusion. We provide finite time performance bounds for the global convergence of NSGLD for solving stochastic non-convex optimization problems. Our results lead to non-asymptotic guarantees for both population and empirical risk minimization problems. Numerical experiments for a simple polynomial function optimization, Bayesian independent component analysis and neural network models show that NSGLD can outperform SGLD with proper choices of the anti-symmetric matrix.